• 
  Алфавит – семь знаков I(1), V(5), X(10), L(50), C(100), D(500), M(1000)
  
• 
  Значение числа равно сумме больших чисел и разности малых чисел, предшествующих большим числам
  
• 
  MCMXCVIII
  

Впервые идея позиционной системы счисления возникла в древнем Вавилоне, Индии и Китае.


В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7•10² + 5•10¹ + 7•10⁰ + 7•10^-1 = 757,7.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д

Например, число сто три представляется в десятичной системе счисления в виде:


Наиболее употребляемыми в настоящее время позиционными системами являются:

• 
  2 — двоичная (информатике, программировании);
  
• 
  3 — троичная;
  
• 
  4 — четверичная;
  
• 
  10 — десятичная (используется повсеместно);
  
• 
  12 — двенадцатеричная (счёт дюжинами);
  
• 
  16 — шестнадцатеричная (в программировании, информатике )
  
• 
  60 — шестидесятеричная (единицы измерения времени).
  

Глава 3. Системы счисления разных народов

Древнеегипетская система счисления

Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия до н.э. Для обозначения чисел 0, 1, 10, 102, 103, 104, 105, 106, 107 использовались специальные цифры. Иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из цифр повторялась не более девяти раз. Значение числа равно простой сумме значений цифр, участвующих в его записи. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека.

---

В основе древнеегипетской системы счисления лежал простой принцип сложения, согласно которому значение числа равно сумме значений цифр, участвующих в его записи. Ученые относят древнеегипетскую систему счисления к десятичной непозиционной.

Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43 они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом, обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне значительно уступали жителям Месопотамии.

Вавилонская система счисления.

Особый интерес представляет так называемая “вавилонская”, или шестидесятеричная система счисления, существовавшая в Древнем Вавилоне. Мнение историков по поводу того, как именно возникла эта система счисления, расходятся. Существуют две гипотезы. Первая исходит из того, что произошло слияние двух племен, одно из которых пользовалось шестеричной, другое – десятичной. Шестидесятеричная система счисления в данном случае могла возникнуть в результате своеобразного политического компромисса. Суть второй гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что связано с числом 60. Отголоски использования этой системы счисления дошли до наших дней. Например, 1 час = 60 минутам. В целом шестидесятеричная система счисления громоздка и неудобна.

В Древнем Вавилоне примерно за сорок веков до нашего времени создалась поместная (позиционная) нумерация, т.е. такой способ изображения чисел, при которой одна и та же цифра может обозначать разные числа в зависимости от места занимаемого этой цифрой. Наша современная нумерация тоже поместная: в числе 52 цифра 5 обозначает пятьдесят, т.е. 5*10, а в числе 576 эта же цифра обозначает пятьсот, т.е. 5*10*10. В вавилонской поместной нумерации ту роль, которую у нас играет число 10, играло число 60. Числа, меньшие 60 обозначались с помощью: для единицы и для десятка.

Привычное нам деление часа и углового или дугового градуса на 60 минут, а одной минуты – на 60 секунд берет начало от вавилонской системы счисления.

---

Во многих календарях считалось, что год состоит из 360 - то есть шести шестидесятков - дней. Встречается это число и в древних сказаниях. Но самое удивительное то, что следы счета шестидесятками сохранились до наших дней. Ведь до сих пор мы делим час на 60 минут, а минуту на 60 секунд. Окружность делят на 360, то есть 6*60 градусов, градус - на 60 минут, а минуту - на шестьдесят секунд. Так что самые точные часы и угломерные приборы хранят в себе память о глубочайшей древности.

Алфавитные системы счисления

Алфавитные системы счисления представляют особую группу. В них для записи чисел использовался буквенный алфавит. Примером алфавитной системы счисления является славянская. У одних славянских народов числовые значения букв устанавливались в порядке следования букв славянского алфавита, у других, в частности у русских, роль цифр играли не все буквы, а только те, которые имеются в греческом алфавите. Над буквой, обозначающей цифру, ставился специальный знак – “титло”. Славянская система счисления сохранилась в богослужебных книгах.
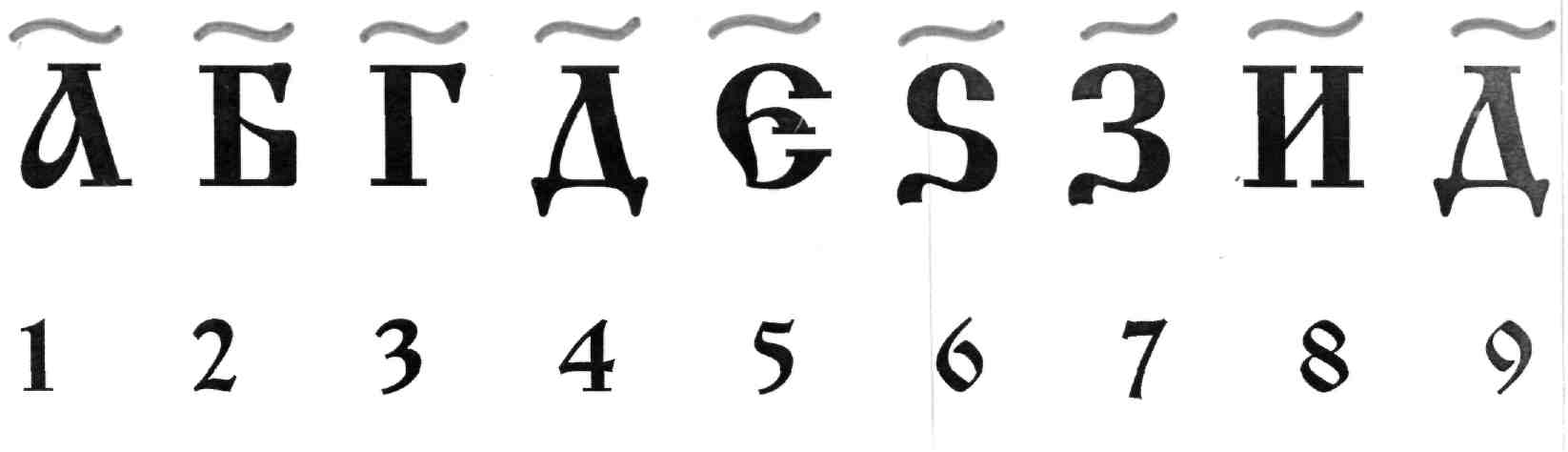Алфавитная нумерация преобладала до XVIII в., хотя арабская нумерация употреблялась в отдельных случаях гораздо раньше (в грузинской литературе такие случаи восходят к X- XI вв.; в памятниках армянской математической литературы они установлены пока только для XV в.). В Армении алфавитная нумерация употребляется и сейчас для обозначения глав в книгах, строф в стихотворениях и т. п. В Грузии алфавитная нумерация вышла из употребления.

Алфавитная система счисления бала распространена у древних армян, грузин, греков (ионическая система счисления), арабов, евреев, и других народов Ближнего востока.

Еврейская система счисления.

Еврейская система счисления в качестве цифр используются 22 буквы еврейского алфавита. Каждая буква имеет своё числовое значение от 1 до 400. «Ноль» отсутствует. Наиболее часто можно встретить цифры, записанные таким образом в нумерации лет по иудейскому календарю.

Система счисления майя.

---

1 2 3 4 5 6 7 8 9 10


У ацтеков и майя – народов, населявших в течение многих столетий обширные области Американского континента и создавших там высочайшую культуру, в том числе и математическую, была принята двадцатеричная система счисления. Также двадцатеричная система счисления бала принята и у кельтов, населявших Западную Европу начиная со второго тысячелетия да нашей эры. Основу для счета в этой системе счисления составляли пальцы рук и ног. Некоторые следы двадцатеричной системы счисления кельтов сохранились во французской денежной системе: основная денежная единица, франк, делится на 20 (1 франк = 20 су)

Майя использовали 20-ричную систему счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году.

Заключение.

В основной части рассмотрены были рассмотрены 10 древних систем счисления, история развития систем счисления. Из всех рассмотренных систем счисления, наиболее интересной мне показалась древне-китайская нумерация. Так как она наиболее близка к нашей «арабской» системе счисления. Наиболее красивые цифры и числа в древнеегипетской системе счисления. В ходе исследования я выяснил каким образом в древности вели устный счет (сложение, вычитание, умножение и деление), а также как использовались счетные доски (например, греческий абак), как с помощью древних цифр происходило представление дробей, какие системы счисления использовали разные народы.

---

Также я выяснил, что двоичная система счисления намного старше электронных машин. Двоичной системой счисления люди интересуются давно. Особенно сильным это увлечение было с конца 16 до 19 века. Знаменитый Лейбниц считал двоичную систему счисления простой, удобной, красивой. Даже по его просьбе была выбита медаль в честь этой «диадической» системы (так называли тогда двоичную систему счисления).Двоичная система счисления наиболее проста и удобна для автоматизации. Наличие в системе всего лишь двух символов упрощает их преобразование в электрические сигналы. Из любой системы счисления можно перейти к двоичному коду. Почти все ЭВМ используют либо непосредственно двоичную систему счисления, либо двоичное кодирование какой-либо другой системы счисления.

Но двоичная система имеет и недостатки:

- ею пользуются только для ЭВМ;

- быстрый рост числа разрядов, необходимых для записи чисел.

Литература

1. Гашков С.Б. Системы счисления и их применение. МЦНМО, 2004г.

2. Угринович Н.Т. Информатика и информационные технологии. Учебник для 10–11 классов. – М.: Лаборатория Базовых Знаний. 2003.

3.Энциклопедия “ВикипедиЯ” [Электронный ресурс]: Режим доступа: http://ru.wikipedia.org, свободный

4.Урнов В.А. и др. Преподавание информатики в компьютерном классе, М.: Просвещение, 1990, стр. 17

5.Заварыкин В.М. Основы информатики и вычислительной техники, М.: Просвещение, 1989, стр.19

6.Гейн А.Г. Основы информатики и вычислительной техники, М.: Просвещение, 1992, стр.231

---

Смотрите также файлы

• Пирамида. Ключевые задачи.doc

• Интерактивное занятие Методика гигиенической оценки температурновлажностного режима.docx

• Содержание Введение Понятия и виды организационных структур Тенденции развития организационных структур Сетевая организационная структура управления Виртуальная структура организации управления Заключение Список литературы Введение.docx

• Готовое решение Как произвести увольнение работника по медицинским показаниям в связи с инвалидностью.rtf

• Экономическая и функциональная стратегии, их типы, факторы выбора. Экономические стратегии наступательная стратегия или стратегия прорыва по направлению подготовки бакалавриата 38. 03. 02 Менеджмент.docx