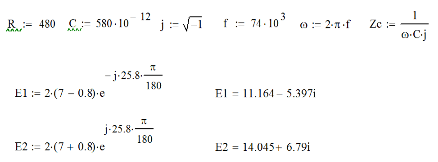Файл: Техническое задание на курсовую работу со схемами 4 Выбор варианта схемы 6.docx

Расчет линейной электрической цепи при гармоническом воздействии

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Целью курсовой работы является изучение базовых методов расчета электрических цепей и развитие умения применять эти методы в решении практических задач по анализу характеристик электрических цепей.

Основными задачами работы являются: расчет значений номиналов элементов электрических цепей, нахождение комплексных амплитуд и мгновенных значений гармонического тока, расчет и построение частотных и переходных характеристик электрических цепей, определение основных параметров указанных величин. Методами решения являются: метод токов ветвей, метод контурных токов, методы анализа частотных и переходных характеристик линейных цепей.

1. Техническое задание на курсовую работу со схемами

В курсовой работе требуется определить токи и напряжения в ветвях простой и сложной электрических цепей при наличии в них источников гармонического напряжения, а также АЧХ и ФХЧ четырехполюсника.

Различные конфигурации схемы образуются в зависимости от положения ключей «К1 - К5», которые устанавливаются по номеру варианта, представленному в двоичном коде.




Определить величины элементов схемы рисунка 1.1 и частоту генераторов с помощью следующих формул

---

где N – номер варианта, n - номер элемента в схеме.

В схеме, полученной в п. 1.1, исключить (замкнуть) все источники кроме и рассчитать, используя простые преобразования цепей, ток в цепи источника . По результатам расчета построить векторную диаграмму для цепи, в которой все элементы цепи, кроме резистора R, подключенного к источнику , объединены в эквивалентное сопротивление , как показано на рисунке 1.2.

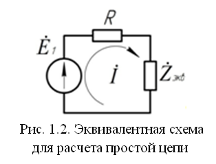
Осуществить моделирование цепи с помощью программы EWB-5.12 и определить значение тока в цепи источника , а также напряжения на сопротивлении и R.

2. Выбор варианта схемы

Для выбора схемы необходимо представить номер варианта в двоичной форме. Установим переключатели К1 - К5 в положения, соответствующие номеру в двоичной записи (Таблица 1).
Таблица 1 - Положение ключей в схеме

Ключи	К1	К2	К3	К4	К5
Двоичная форма записи числа 4	0	0	1	0	0
Положение ключей	0	0	1	0	0

Зарисуем получившуюся схему без переключателей и отсоединенных элементов.


Рис.2.1. Схема электрической цепи в соответствии

---

Определим величины элементов схемы (Рисунок 2.1) по формулам из п. 1.2, учитывая, что все генераторы в схеме имеют одинаковую частоту:

R = 100·(4+0,2·4) = 480 Ом;

С = 100·(5+0,2·4) = 580 пФ;
Ė1 = 2·[7+(-1)¹⁺⁴·0.2·4] ·е^{(-1)·j(25+0,2·4)} = 12,4·е^{- j 25,8} В;

Ė2 = 2·[7+(-1)²⁺⁴·0.2·4] ·е^j(25+0,2·4) = 15,6·е ^{j 25,8} В;

Ė3 = 2·[7+(-1)³⁺⁴·0.2·4] · е^{(-1)·j(25+0,2·4)} = 12,4·е ^{-j 25,8} В;

Ė4 = 2·[7+(-1)⁴⁺⁴·0.2·4] ·е^j(25+0,2·4) = 15,6·е ^{j 25,8} В;

Ė5 = 2·[7+(-1)⁵⁺⁴·0.2·4] · е^{(-1)·j(25+0,2·4)} = 12,4·е ^{-j 25,8} В;

fn = 10[7+(-1)⁴·0.2·4] = 78кГц.
В соответствии с заданием все генераторы имеют одинаковую частоту:
f1 = f2 = f3 = f4 = f5 =78кГц.
Значение фазы источников задается в градусах, а Mathcad осуществляет расчеты в радианах. Вследствие этого величину фазы генераторов умножаем на величину .

3. Расчет простой электрической цепи

В схеме (рис. 2.1) замкнем все источники кроме (см. рис. 3.1):


Рис.3.1. Схема цепи с одним источником
Преобразуем данную схему, объединив все элементы цепи, кроме R, подключенного к источнику , в эквивалентное сопротивление

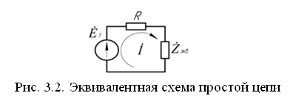
Рассчитаем, используя простые преобразования цепей, ток в цепи источника , а также напряжения на R и .

Значение тока в цепи источника определяется по формуле закона Ома для полной цепи:

Эквивалентное сопротивление

---

_экв определим, используя формулы для последовательного и параллельного соединения нескольких элементов.

Напряжение на сопротивлении _экв определяется по формуле:
_экв
Напряжение на сопротивлении R определяется по формуле:

Все необходимые расчеты проведем в среде Mathcad




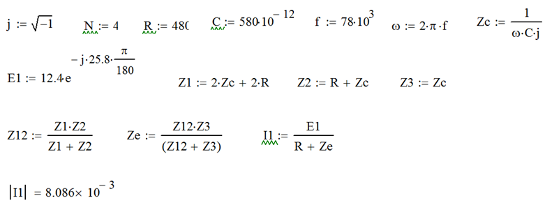
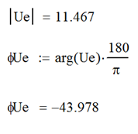
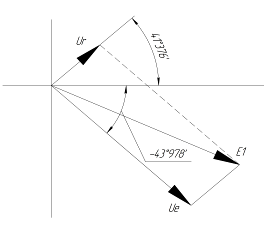
По полученным значениям строим векторную диаграмму в масштабе для , , , Ė₁, имея в виду, что в цепи выполняется второй закон Кирхгофа, т.е.
,
а для векторов это отражается в виде их векторной суммы.

Построим векторную диаграмму.

Проведем моделирование режима работы простой цепи с помощью программы EWB 5.12. Соберем простую цепь в соответствии с рис. 3.1. Выберем номиналы резисторов и конденсаторов в соответствии с заданием. Установим величину ЭДС, частоты и начальной фазы генератора, учтем что в программе EWB 5.12 гармоническое напряжение задается в синусоиде и увеличим угол на 90⁰.

Результаты моделирования в EWB:

Результаты сравниваем с рассчитанными ранее значениями аргументов

---

Сравнение результатов расчета и моделирования простой схемы

Рассчитываемая величина	В системе Mathcad	В системе EWB-5.12	Погрешность
I, мА	8,086	7,885	0,201
, В	11,476	11,27	0,206
, В	3,881	3,783	0,098

Малая погрешность расчетов позволяет сделать вывод о достоверности результатов.

4. Составление системы уравнений для расчета токов и напряжений

Для определения токов и напряжений на всех элементах цепи при известных значениях R, C и E необходимо составить систему уравнений по методу контурных токов. Данный метод основан на использовании только второго закона Кирхгофа, что позволяет уменьшить число уравнений, которые нужно решать совместно. Схема электрической цепи, токи в которой необходимо определить представлена на рис. 4.1.


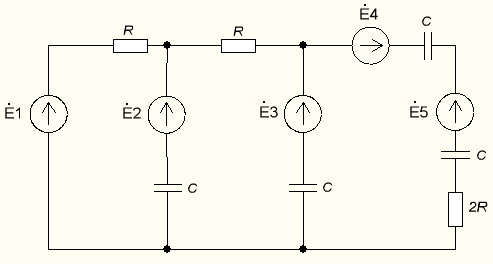
Рис.4.1 Схема цепи для расчета токов и напряжений

Вначале составляется граф данной электрической цепи, по которому выбираются независимые контуры и задаются контурные токи. Для этих контуров составляются уравнения по второму закону Кирхгофа с учетом совместного влияния одного контура на другой. Направления обхода во всех контурах выбирают одинаковыми.

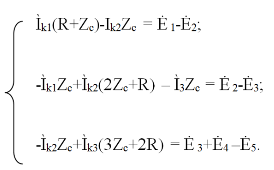
5. Расчет контурных токов в сложной электрической цепи методом Крамера и обратной матрицы

Расчеты проведенные в среде Mathcad

---