Файл: Реферат по инженерной графике по теме Проекционное черчение студентка гр. Тэп18зп Коногорова А. О.docx
Добавлен: 11.04.2024
Просмотров: 55
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Е и F на рис. 4.1). Обычно для их определения используют вспомогательные параллельные секущие плоскости (рис. 4.1, а).
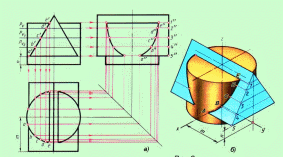
Рисунок 4.2 - Линии пересечения треугольной призмы и цилиндра
В качестве вспомогательных плоскостей выбирают такие плоскости, которые пересекают обе заданные поверхности по простым линиям – прямым или окружностям, причем окружности должны располагаться в плоскостях, параллельных плоскостям проекций.
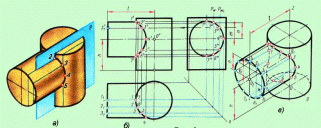
Рисунок 4.3 - Линии пересечения двух цилиндров
В примере, показанном на рис. 4.1, в, плоскость Р рассекает конус по окружности, с помощью которой находят горизонтальные проекции точек e и f.
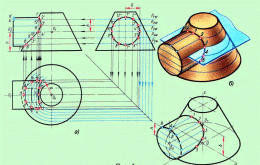
Рисунок 4.4 - Линии пересечения конуса и цилиндра
Во всех случаях перед тем, как строить линию пересечения поверхностей на чертеже, необходимо представить себе эту линию в пространстве (рис. 4.1, б).
На рисунках 4.2 и 4.4 показаны примеры построения линии пересечения треугольной призмы и цилиндра, а также конуса и цилиндра с помощью вспомогательных горизонтальных секущих плоскостей.
На рисунках 4.3 и 4.5 показаны примеры построения линии пересечения двух цилиндров, а также цилиндра и тора с использованием вспомогательных вертикальных секущих плоскостей.
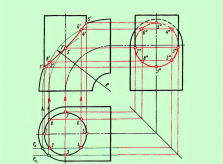
Рисунок 4.5 - Линии пересечения цилиндра и тора
В некоторых случаях для построения линий пересечения геометрических тел удобно применять способ вспомогательных сфер. В отличие от способа вспомогательных секущих поверхностей метод вспомогательных сфер имеет определенное преимущество, поскольку при построении фронтальной проекции линии пересечения поверхностей не используются другие проекции пересекающихся поверхностей геометрических тел (рис. 4.6).
Вспомогательные сферические поверхности для построения линий пересечения геометрических тел можно применять лишь при следующих условиях:
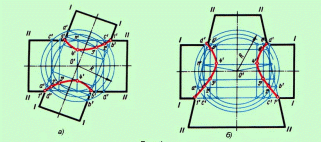
Рисунок 4.6 - Построение линии пересечения геометрических тел:
а). двух цилиндров; б). конуса и цилиндра.
Примеры применения вспомогательных сфер при построении линии пересечения геометрических тел приведены на рис. 4.6 а, б.
На рис. 4.6, а показано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом. Вспомогательные сферы проводят из точки О' пересечения осей цилиндров.
Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересечения. Для этого из точки О' проводят сферическую поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса.
Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра АС и ВD, а наклонно расположенный цилиндр – по окружностям диаметра АВ.
В пересечении полученных проекций окружностей – отрезков a’b’ и c’d’ – находят проекцию 2' промежуточной точки линии пересечения.
Вспомогательные сферы могут иметь радиусы в определенных пределах, позволяющих использовать их для построения общих точек пересекающихся тел. Пределы радиусов вспомогательных сфер находят следующим образом (рис. 4.6, а и б):
Если поверхности двух конусов (рис. 4.7) описаны около шара, то они касаются шара по двум окружностям, которые пересекаются в двух точках. Эти точки проецируются на фронтальную плоскость проекций в точку р'. Плоскости, в которых лежат эти окружности, пересекаются по прямой, соединяющей точки пересечения линий касания конусов с шаром.
Окружности проецируются на фронтальную плоскость проекций в виде прямых линий.
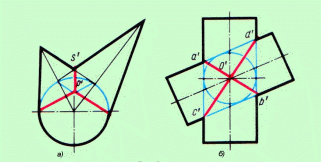
Рисунок 4.7 - Построение линии пересечения геометрических тел:
а). конусов с шаром; б). два прямых круговых цилиндра.
Соединив очевидную точку s’ пересечения конусов с точкой р', получим линию пересечения конусов с шаром, которая представляет собой фронтальную проекцию эллипса.
Разберем второй подобный пример.
Если два прямых круговых цилиндра с осями, пересекающимися в точке
О' (рис. 4.7, б), описаны около шара с центром в точке О, то фронтальная проекция шара будет окружностью, касательной к контурным образующим цилиндров.
Линии пересечения поверхностей этих цилиндров представляют собой эллипсы, фронтальные проекции которых изображаются в виде прямых линий a’b’ и c’d’.
1. Бударин О.С. Начертательная геометрия. Краткий курс : учеб. пособие / О.С. Бударин, 2019 г.
2. Королев Ю.И. Начертательная геометрия : учеб. / Ю.И. Королев, 2019 г.
3. Лагерь А.И. Основы начертательной геометрии : учебник для техн. вузов / А.И. Лагерь, А.Н. Мота, К.С. Рушелюк, 2019 г.
4. Локтев О.В. Краткий курс начертательной геометрии : учебник / О.В. Локтев, 2019 г.
5. Нартова Л.Г. Начертательная геометрия : учеб. / Л.Г. Нартова, В.И. Якунин, 2019 г.
6. Тарасов Б. Ф. Начертательная геометрия: учебник / Б.Ф. Тарасов, Л.А. Дудкина, С.О. Немолотов, 2019 г.
7. Чекмарев А.А. Начертательная геометрия и черчение: учеб. / А.А. Чекмарев, 2019 г.

Рисунок 4.2 - Линии пересечения треугольной призмы и цилиндра
В качестве вспомогательных плоскостей выбирают такие плоскости, которые пересекают обе заданные поверхности по простым линиям – прямым или окружностям, причем окружности должны располагаться в плоскостях, параллельных плоскостям проекций.

Рисунок 4.3 - Линии пересечения двух цилиндров
В примере, показанном на рис. 4.1, в, плоскость Р рассекает конус по окружности, с помощью которой находят горизонтальные проекции точек e и f.

Рисунок 4.4 - Линии пересечения конуса и цилиндра
Во всех случаях перед тем, как строить линию пересечения поверхностей на чертеже, необходимо представить себе эту линию в пространстве (рис. 4.1, б).
На рисунках 4.2 и 4.4 показаны примеры построения линии пересечения треугольной призмы и цилиндра, а также конуса и цилиндра с помощью вспомогательных горизонтальных секущих плоскостей.
На рисунках 4.3 и 4.5 показаны примеры построения линии пересечения двух цилиндров, а также цилиндра и тора с использованием вспомогательных вертикальных секущих плоскостей.

Рисунок 4.5 - Линии пересечения цилиндра и тора
4.3 Построение линий пересечения поверхностей способом вспомо
гательных сфер
В некоторых случаях для построения линий пересечения геометрических тел удобно применять способ вспомогательных сфер. В отличие от способа вспомогательных секущих поверхностей метод вспомогательных сфер имеет определенное преимущество, поскольку при построении фронтальной проекции линии пересечения поверхностей не используются другие проекции пересекающихся поверхностей геометрических тел (рис. 4.6).
Вспомогательные сферические поверхности для построения линий пересечения геометрических тел можно применять лишь при следующих условиях:
-
пересекающиеся поверхности должны быть поверхностями тел вращения; -
оси поверхностей вращения должны пересекаться, при этом точка пересечения осей является центром вспомогательных сфер; -
оси поверхностей вращения должны быть параллельны какой-нибудь из плоскостей проекций.

Рисунок 4.6 - Построение линии пересечения геометрических тел:
а). двух цилиндров; б). конуса и цилиндра.
Примеры применения вспомогательных сфер при построении линии пересечения геометрических тел приведены на рис. 4.6 а, б.
На рис. 4.6, а показано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом. Вспомогательные сферы проводят из точки О' пересечения осей цилиндров.
Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересечения. Для этого из точки О' проводят сферическую поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса.
Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра АС и ВD, а наклонно расположенный цилиндр – по окружностям диаметра АВ.
В пересечении полученных проекций окружностей – отрезков a’b’ и c’d’ – находят проекцию 2' промежуточной точки линии пересечения.
Вспомогательные сферы могут иметь радиусы в определенных пределах, позволяющих использовать их для построения общих точек пересекающихся тел. Пределы радиусов вспомогательных сфер находят следующим образом (рис. 4.6, а и б):
-
окружность сферы наибольшего радиуса должна пересекаться с контурными образующими I-I и II-II цилиндров; -
окружность сферы наименьшего радиуса должна быть касательной к одной из данных пересекающихся поверхностей и обязательно пересекаться с образующими других поверхностей.
Если поверхности двух конусов (рис. 4.7) описаны около шара, то они касаются шара по двум окружностям, которые пересекаются в двух точках. Эти точки проецируются на фронтальную плоскость проекций в точку р'. Плоскости, в которых лежат эти окружности, пересекаются по прямой, соединяющей точки пересечения линий касания конусов с шаром.
Окружности проецируются на фронтальную плоскость проекций в виде прямых линий.

Рисунок 4.7 - Построение линии пересечения геометрических тел:
а). конусов с шаром; б). два прямых круговых цилиндра.
Соединив очевидную точку s’ пересечения конусов с точкой р', получим линию пересечения конусов с шаром, которая представляет собой фронтальную проекцию эллипса.
Разберем второй подобный пример.
Если два прямых круговых цилиндра с осями, пересекающимися в точке
О' (рис. 4.7, б), описаны около шара с центром в точке О, то фронтальная проекция шара будет окружностью, касательной к контурным образующим цилиндров.
Линии пересечения поверхностей этих цилиндров представляют собой эллипсы, фронтальные проекции которых изображаются в виде прямых линий a’b’ и c’d’.
Список используемой литературы:
1. Бударин О.С. Начертательная геометрия. Краткий курс : учеб. пособие / О.С. Бударин, 2019 г.
2. Королев Ю.И. Начертательная геометрия : учеб. / Ю.И. Королев, 2019 г.
3. Лагерь А.И. Основы начертательной геометрии : учебник для техн. вузов / А.И. Лагерь, А.Н. Мота, К.С. Рушелюк, 2019 г.
4. Локтев О.В. Краткий курс начертательной геометрии : учебник / О.В. Локтев, 2019 г.
5. Нартова Л.Г. Начертательная геометрия : учеб. / Л.Г. Нартова, В.И. Якунин, 2019 г.
6. Тарасов Б. Ф. Начертательная геометрия: учебник / Б.Ф. Тарасов, Л.А. Дудкина, С.О. Немолотов, 2019 г.
7. Чекмарев А.А. Начертательная геометрия и черчение: учеб. / А.А. Чекмарев, 2019 г.

