Файл: Проверка таблицы истинности основных логических элементов.docx

Факультет «Компьютерных технологии и кибербезопасности»

Кафедра «Радиотехники, электроники и телекоммуникации»

Лабораторная работа №1

По дисциплине: Цифровые устройства и микропроцессоры

На тему: Проверка таблицы истинности основных логических элементов

Выполнила: студентка группы ССТ-2002 Куатова Венера

Проверил: сениор-лектор Джапаркулов Б.К.

Алматы, 2023

2.1 Лабораторная работа № 1. ПРОВЕРКА ТАБЛИЦЫ ИСТИНОСТИ ОСНОВНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ

2.1.1 Цель работы

Целью лабораторной работы является экспериментальное получение таблиц соответствия (таблиц истинности) логических элементов И (AND), НЕ (NOT), ИЛИ (OR), И-НЕ (NOT-AND), ИЛИ-НЕ (NOT-OR), исключающее ИЛИ (XOR), исключающее ИЛИ-НЕ (XNOR).

2.1.2 Краткие сведения из теории

Математической основой цифровых вычислительных устройств является двоичная арифметика, в которой используется всего два числа – 0 и 1. Выбор двоичной системы счисления диктовался требованиями простоты технической реализации самых сложных задач с использованием всего одного базового элемента – ключа, который имеет два состояния: включен (замкнут) или выключен (разомкнут). Если первое состояние ключа принять за условную (логическую) единицу, то второе будет отражать условный (логический) ноль или наоборот.

Итак, переменные, рассматриваемые в алгебре логики, могут принимать только два значения – 0 или 1.
В алгебре логики определены: отношение эквивалентности (F=A), и операции:

– логического сложения (дизъюнкции) F=А+В; (ИЛИ)

– логического умножения (конъюнкции) F=А*В; (И)

– отрицания (инверсии) F= 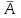. (НЕ)

– логического сложения с инверсией (функция Пирса) F= 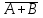; (ИЛИ–НЕ)

– логического умножения с инверсией (функция Шеффера) F= 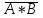; (И–НЕ)

– неравнозначности F= 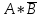+ 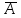*В=А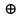

---

В; (исключающее ИЛИ)

• 
  равнозначности F=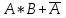 * 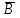= 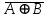; (исключающее ИЛИ-НЕ).
  

В приведенных выше функциях входными переменными являются А и В, выходной переменная F.

Каждой из этих функций соответствует свой логический элемент.

На рисунке 2.1 приведены 2-входовые логические элементы (исключение элемент «НЕ», у него 1 вход) используемые в ППП Electronics Workbench.

Все логические элементы могут иметь любое количество входов и описываться аналогичными функциями, например работу 3-входового элемента «ИЛИ» (3ИЛИ) можно описать функцией F=A+B+C. Исключением является элемент «НЕ», который всегда имеет только 1 вход.



Рисунок 2.1 Графическое обозначение логических элементов по ANSI
Данные обозначения элементов применяются в западных странах. В отечественной же промышленности применяют обозначения, показанные на рисунке 2.2.

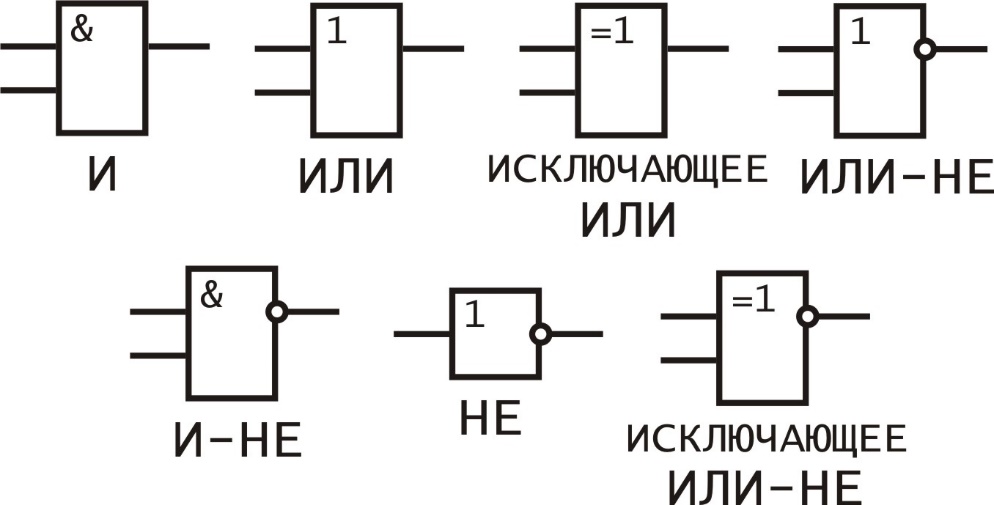
Рисунок 2.2 УГО логических элементов по ГОСТ
Для построения многовходовых элементов в ППП Electronics Workbench необходимо зайти в свойства элемента, количество входов которого вы хотите изменить (нажать правой кнопкой мышки на элементе, выбрать пункт Component Properties…), выбрать вкладку «Количество входов» (Number of Inputs) (рисунок 2.3), и выбрать требуемое количество входов (от 2 до 8).

Так как область определения любой двоичной функции N-переменных конечна (2ⁿ - значений), такая функция может быть задана таблицей значений F(x_i), которые она принимает в точках x_i, где i=0,1,2,.. 2^n-1 – номер опыта. Такие таблицы называют таблицами истинности (таблица 2.1) .
Таблица 2.1 Таблица истинности двухвходового элемента

i	X1	X0	F(xi)
0	0	0
1	0	1
2	1	0
3	1	1

---

Рисунок 2.3 Окно, в котором указывается количество входов логического элемента

2.1.3 Содержание лабораторной работы

Задание:

1) Исследовать логические функции И, НЕ, ИЛИ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ, исключающее ИЛИ-НЕ, используя типовые компоненты ППП Electronics Workbench.

2) Заполнить таблицу истинности логических функций от двух переменных (таблица 2.2).

Таблица 2.2 Бланк для заполнения таблицы истинности

i	А	В	F=А+В	F=	F=А*В	F=	F=А В	F=
0	0	0	0	1	0	1	0	1
1	0	1	1	1	0	1	1	0
2	1	0	1	0	0	1	1	0
3	1	1	1	1	1	0	0	1

Порядок выполнения:

1. 
   Загрузить ППП Electronics Workbench.
   
2. 
   Реализовать на ключах и логических элементах, типовые логические функции, представленные на рисунках 2.4…2.9.
   
3. 
   Результаты исследования занести в таблицу 2.2.
   

Примечание: Порядок доступа до компонентов, используемых в лабораторной работе приведен в разделе 1.2.2, рисунок 1.2.2.

---

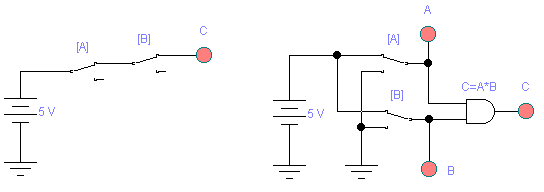
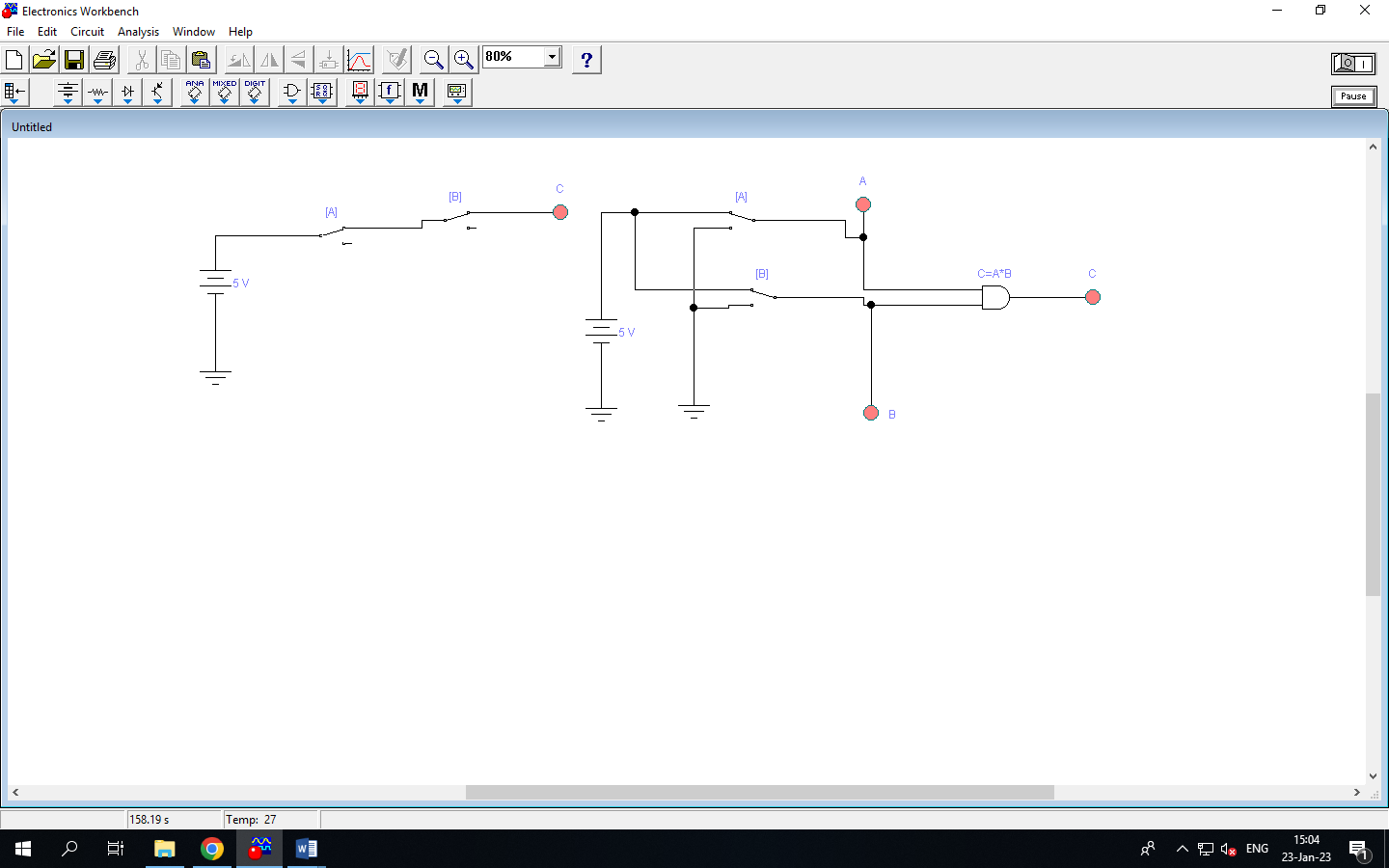
Рисунок 2.4 Логическая функция – И



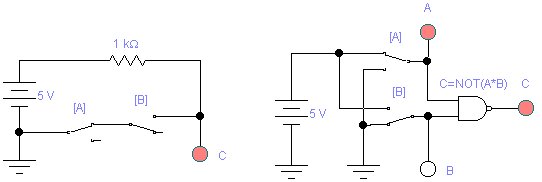
Рисунок 2.5 Логическая функция – И–НЕ



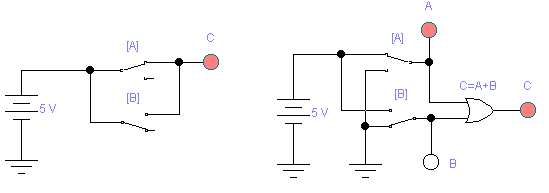
Рисунок 2.6 Логическая функция – ИЛИ



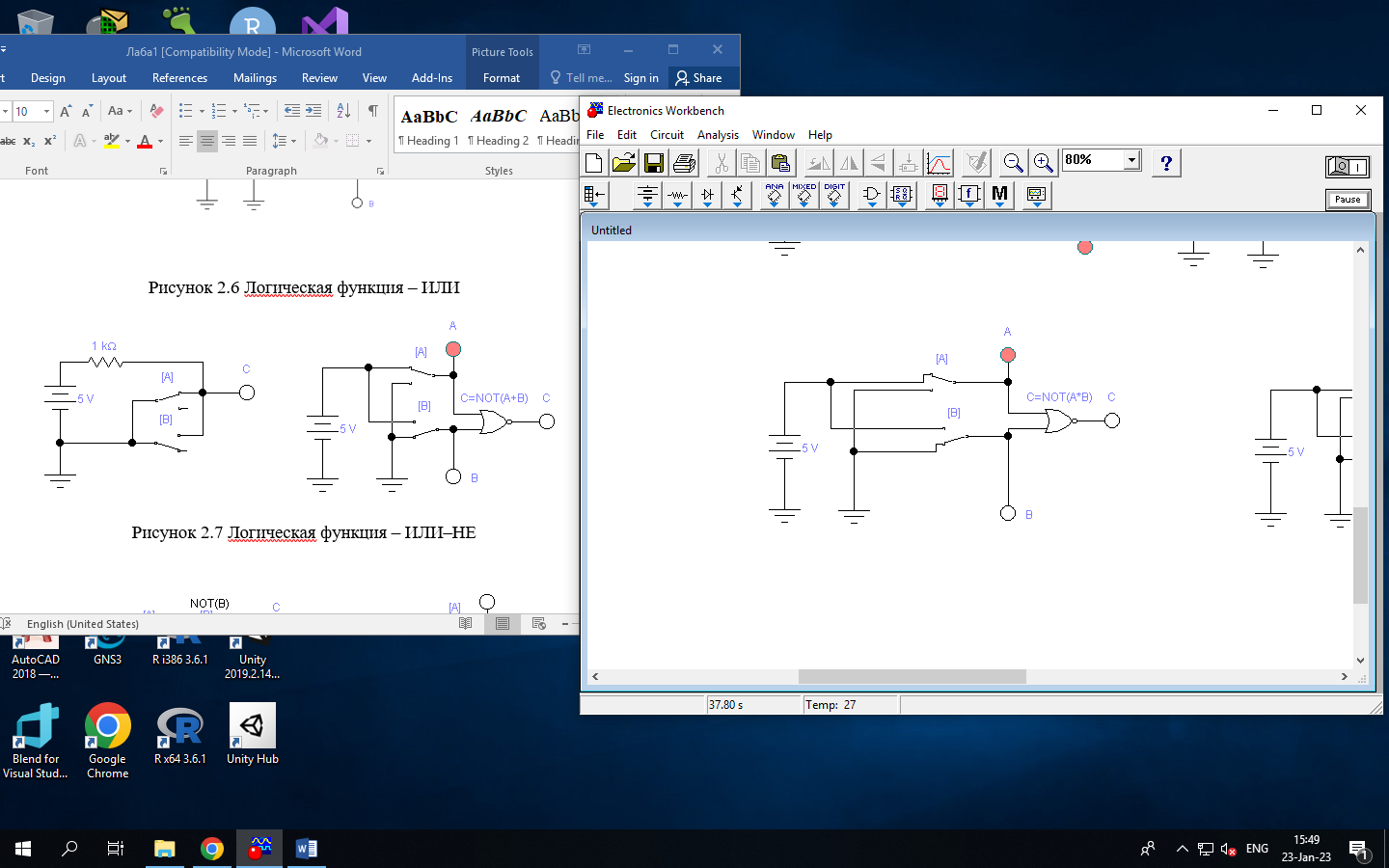
Рисунок 2.7 Логическая функция – ИЛИ–НЕ



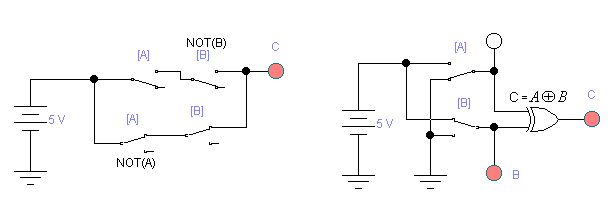
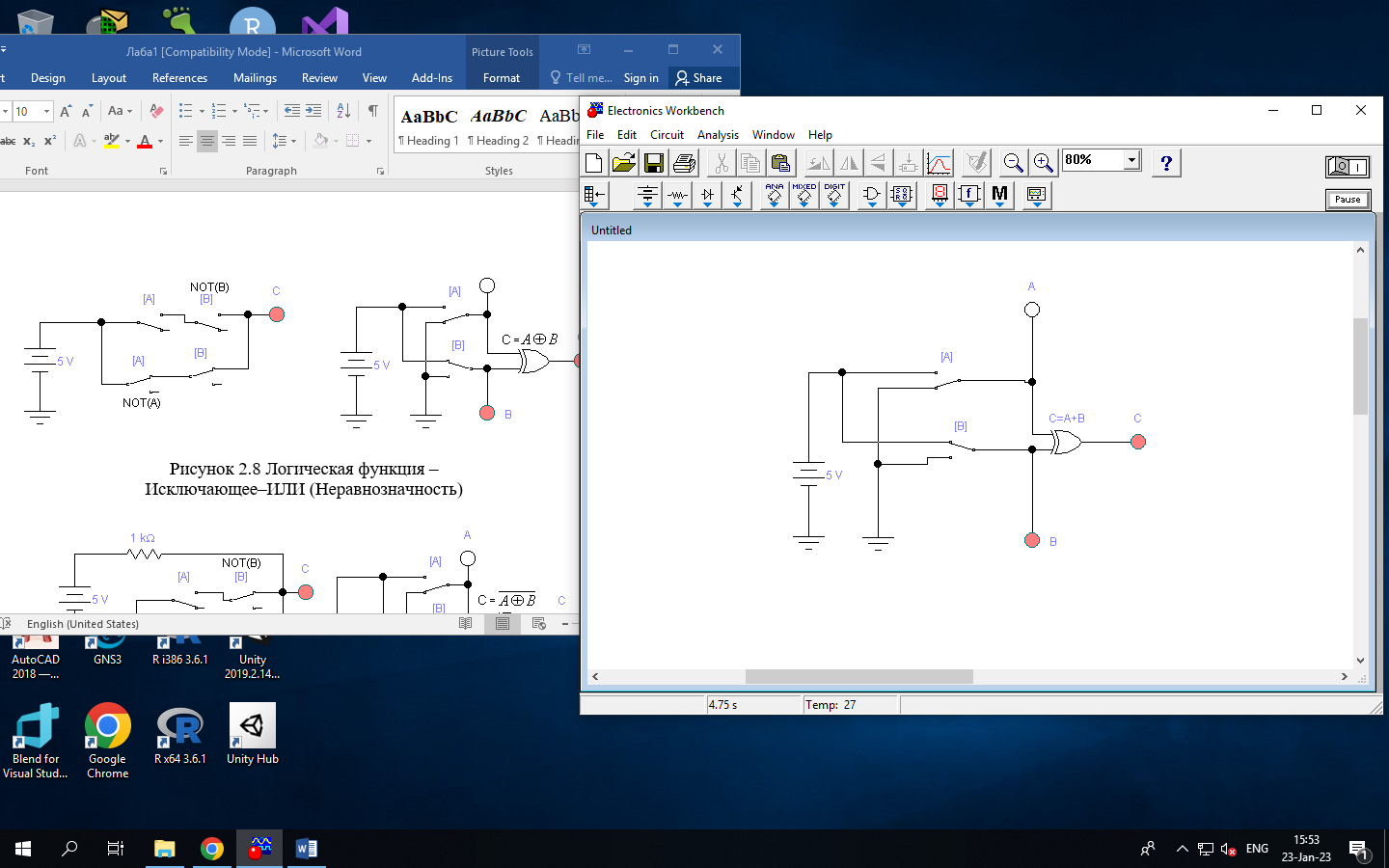
Рисунок 2.8 Логическая функция –

Исключающее–ИЛИ (Неравнозначность)



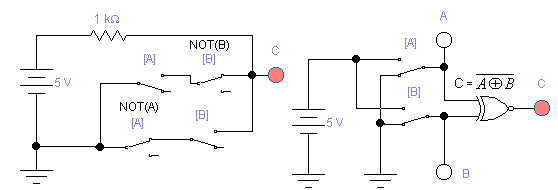
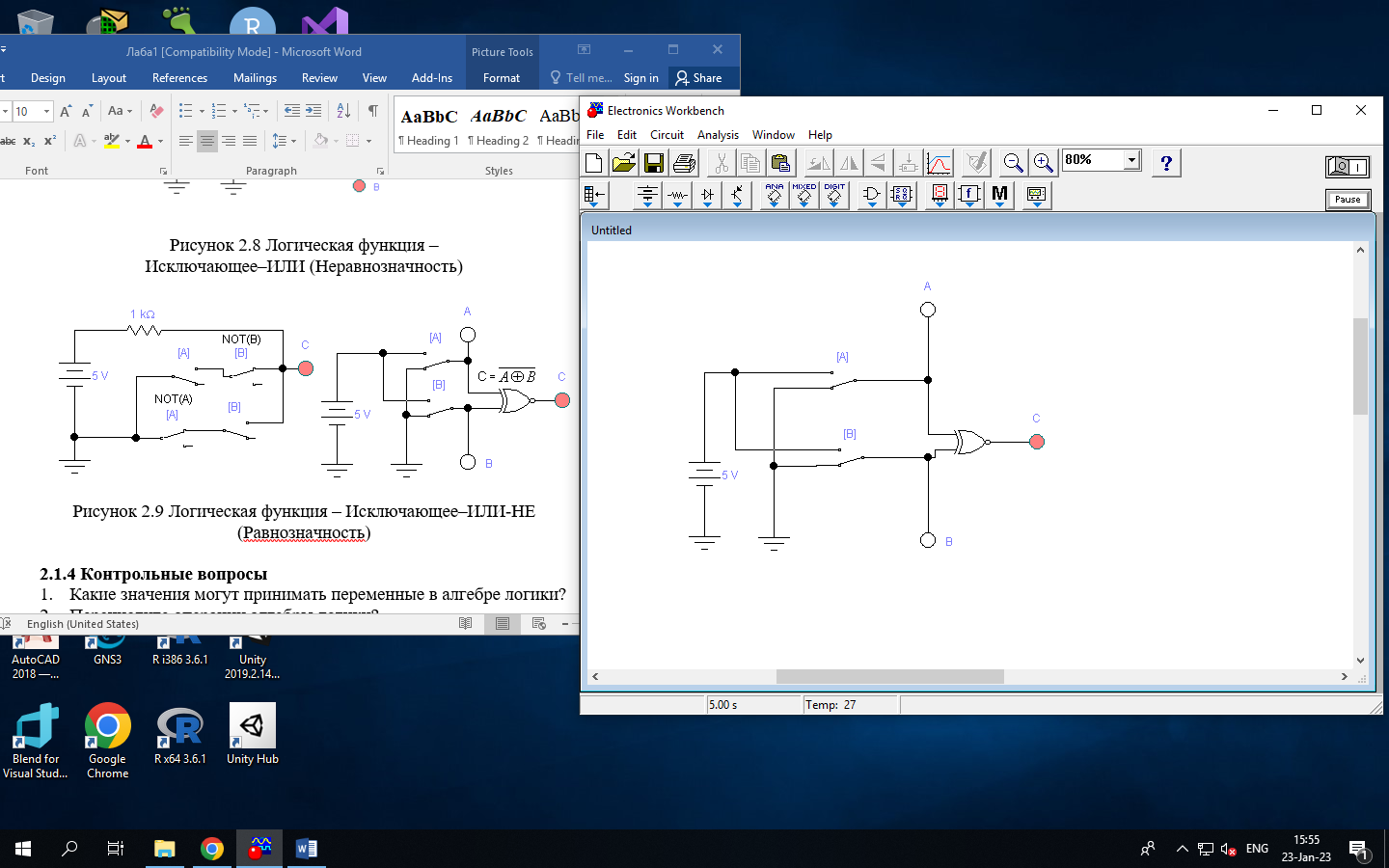
Рисунок 2.9 Логическая функция – Исключающее–ИЛИ-НЕ

(Равнозначность)

2.1.4 Контрольные вопросы

1. 
   Какие значения могут принимать переменные в алгебре логики?
   

0 и 1

2. 
   Перечислите операции алгебры логики?
   

ИЛИ дизъюнкция, И конъюнкция, НЕ инверсия , ИЛИ-НЕ импликация, И-НЕ , иск ИЛИ, иск ИЛИ-НЕ эквивалентность.

3. 
   Графическое обозначение логических элементов.
   

4. 
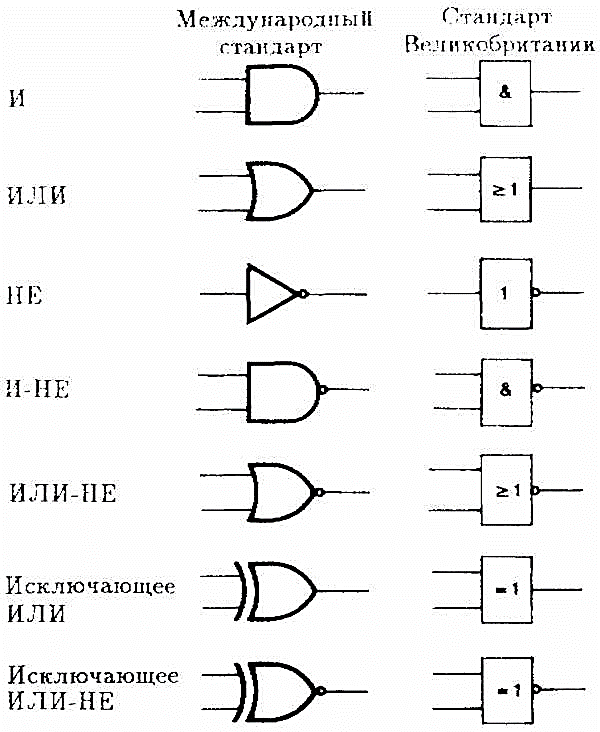
   Каким может быть число входов элемента "НЕ"?
   

Логический элемент «Не», также называемый «инвертор», «отрицание», «Not», выполняет над входными данными логическое отрицание. Этот элемент имеет один вход и один выход.

5. 
   Каким может быть число входов элемента "И"?
   

Число входов логических элементов И может быть любым начиная с двух.

6. 
   Каким может быть число входов элемента "ИЛИ"?
   

Число входов логических элементов ИЛИ может быть любым начиная с двух.

---

7. 
   Каким может быть число входов элемента "И-НЕ"?
   

Выпускаемые в настоящее время вентили И-НЕ имеют в основном от 2 до 4 входов. Изредка встречаются вентили с 8 и более входами.

8. 
   Каким может быть число входов элемента "ИЛИ-НЕ"?
   

Число входов элемента "ИЛИ-НЕ" (NOR) может быть любым, так как этот элемент является комбинацией логического "ИЛИ" и логического "НЕ", и может иметь неограниченное число входов.

9. 
   Каким может быть число входов элемента "Исключающее ИЛИ"?
   

Число входов элемента "Исключающее ИЛИ" (XOR) так же может быть любым, так как этот элемент может иметь неограниченное число входов.

10. 
    Каким символом обозначается логический элемент, реализующий операцию логического умножения:
    

B)  ;

11. 
    Каким символом обозначается логический элемент, реализующий операцию логического сложения:
    

E) 1.

12. 
    Каким символом обозначается логический элемент, реализующий операцию "сложения по модулю 2":
    

D) =1 ;

13. 
    При какой входной комбинации элемент 3И даст логическую единицу на выходе?
    

D) 111;

14. 
    При какой входной комбинации элемент 3ИЛИ даст логический ноль на выходе?
    

B) 000;

15. 
    При какой входной комбинации элемент 3И-НЕ даст логический ноль на выходе?
    

C) 111;

16. 
    При какой входной комбинации элемент "3ИЛИ-НЕ" даст логическую единицу на выходе?
    

B) 111;

17. 
    Аналогично какому логическому элементу работает схема с параллельно включенными ключами:
    

C) И

18. 
    Аналогично какому логическому элементу работает схема с последовательно включенными ключами:
    

D) ИЛИ;

19. 
    Какой из логических элементов дает на выходе «1» только в том случае, когда сигналы на двух входах неодинаковы?
    

ИСКЛЮЧАЮЩЕЕ ИЛИ

2.1.5 Список рекомендуемой литературы

1. 
   Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и ее применение. – М.: Солон, 1999.- 512 с.
   
2. 
   Криштрафович А.К. Промышленная электроника: Учебник для учащихся электрорадиотехн. и электроприборостроит. спец. техникумов. – М.: Высшая школа, 1984. – 351 с.
   
3. 
   Основы промышленной электроники/ Под ред. Герасимова В.Г. – М.: Высшая школа, 1986.- 336 с.
   

---