Файл: Курсовая работа по дисциплине электротехника.docx

Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Кафедра АТМ
КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ «ЭЛЕКТРОТЕХНИКА»
Вариант № 2
Выполнил:
Проверил:
доцент каф. АТМ		/ А. И. Ишемгужин /
Оценка ____________/ А. И. Ишемгужин /
Уфа 2022

СОДЕРЖАНИЕ

Исходные данные

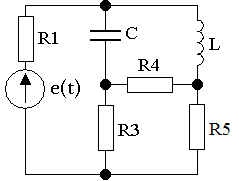
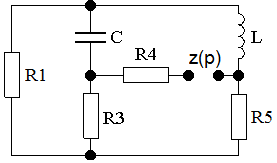
Выполнить анализ процессов в электрической цепи второго порядка по данным таблицы 1 и схеме на рисунке 1.

Таблица 1 – Параметры элементов цепи

Номер варианта	Номер рисунка	R2, Ом	R3=R5, Ом	R1=R4, Ом	L, Гн	C, мкФ	E, В	f, Гц	φ, рад
2	2	50	80	100	1,0	15	140	100	-π/4

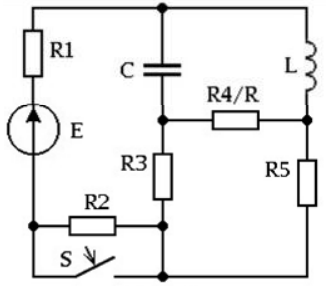
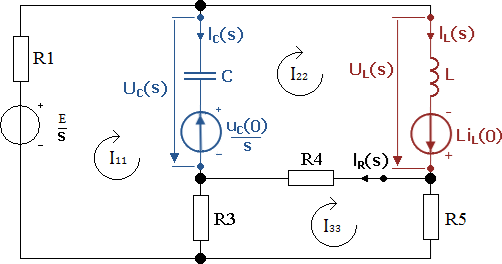
Рисунок 1 – Обобщенная схема цепи

Задание 1 Расчет начальных условий

В цепи действует постоянная э.д.с. e(t) = E.

1) Ключ S разомкнут. Рассчитать методами анализа электрических цепей постоянного тока: u

---

_С(0)_ – напряжение на конденсаторе; i_L(0)_ – ток в ветви с катушкой индуктивности; i_R(0)_ – ток в резисторе R, отмеченный в схеме.

2) Ключ S замкнут. Рассчитать методами анализа электрических цепей постоянного тока: u_C(∞) – напряжение на конденсаторе; i_L(∞) – ток в ветви с катушкой индуктивности; i_R(∞) – ток в резисторе R, отмеченный в схеме.

1. Собираем схему в EWB и находим все значения искомых величин, измеряя их при помощи амперметров и вольтметров.

t= 0 -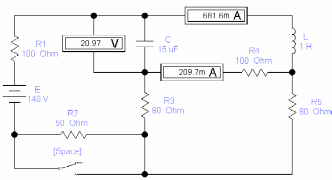
t= 0 +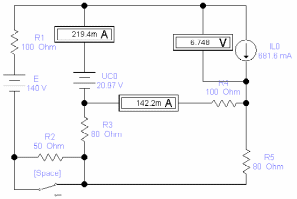
t= ∞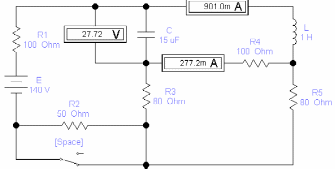

2. Получим все значения искомых величин аналитическим путем

t= 0 -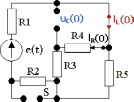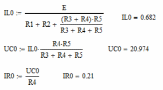
t= 0 +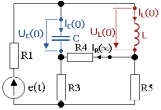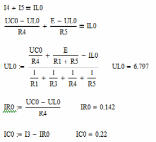
t= ∞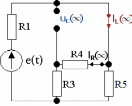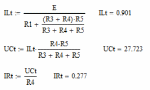

3. Сравниваем полученные значения

Время, с	Переменная	Метод расчета
		С помощью амперметров и вольтметров в EWB	Аналитический расчет в MathCAD
t = 0-	IL(0-), А	0.682	0.682
	UC(0-), В	20.974	20.974
	IR(0-), А	0.21	0.2097
t = 0+	UL(0+), В	6.797	6.797
	IC(0+), А	0.22	0.219
	IR(0+), А	0.142	0.142
t = ∞	IL(∞), А	0.901	0.901
	UC(∞), В	27.723	27.723
	IR(∞), А	0.277	0.277

---

Вывод: были рассчитаны начальные условия тока на индуктивности L, напряжения на емкости С и тока на отмеченном резисторе R в при разомкнутом ключе (t=0-), при замыкании ключа (t = 0+) и при замкнутом ключе (t = ∞), в результате чего решение, отраженное в MathCAD совпадает с полученными значениями в Electronics Workbench.

Задание 2 Расчет цепей синусоидального переменного тока по комплексным значениям

В цепи действует синусоидальная э.д.с.:



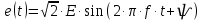
Необходимо:

1) Рассчитать комплексным методом установившийся режим в цепи при замкнутом ключе S. Найти зависимости в виде функций времени:

– u_C(t) – напряжение на конденсаторе;

– i_L(t) – ток в ветви с катушкой индуктивности;

– i_R(t) – ток в резисторе R, отмеченный в схеме.

2) Построить векторные диаграммы рассчитанных токов и напряжения.

Исходные данные:

1. 
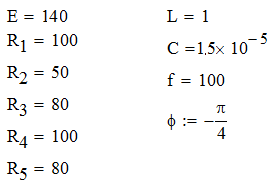
   Расчет комплексов исходных величин
   

1. 
   Определим комплексное сопротивления элементов схемы:
   

2. 
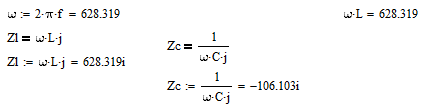
   Расчет контурных токов:
   

3. 
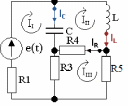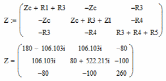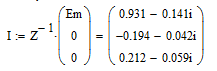
   Расчет искомых токов и напряжения в ветвях:
   

4. 
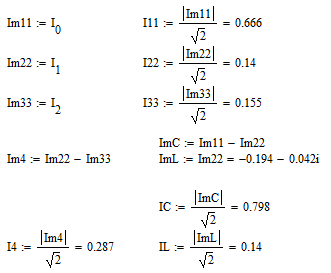
   Расчет искомых функциональных зависимостей
   

Определение зависимости в виде функций времени:

---

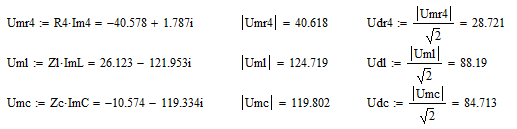
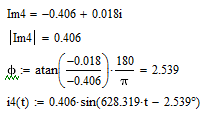
Графики синусоидальных функций

2. 
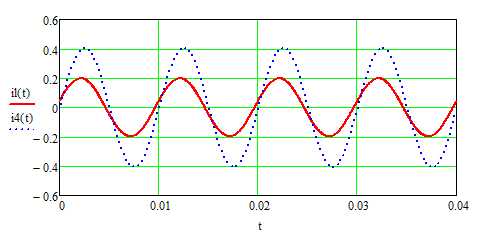
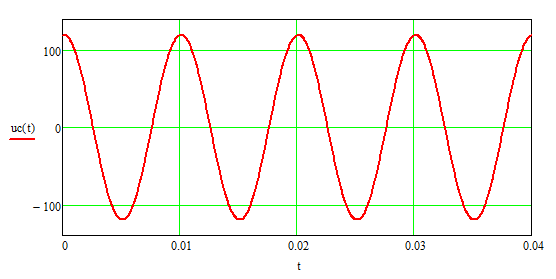
   Построение векторной диаграммы
   

1. 
   Построение векторной диаграммы для токов:
   

2. 
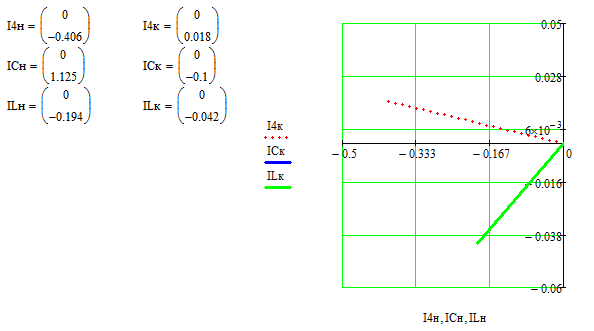
   Построение векторной диаграммы для напряжения на конденсаторе:
   

3. 
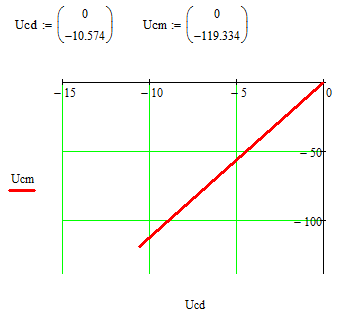
   Проверка результатов расчета в EWB:
   

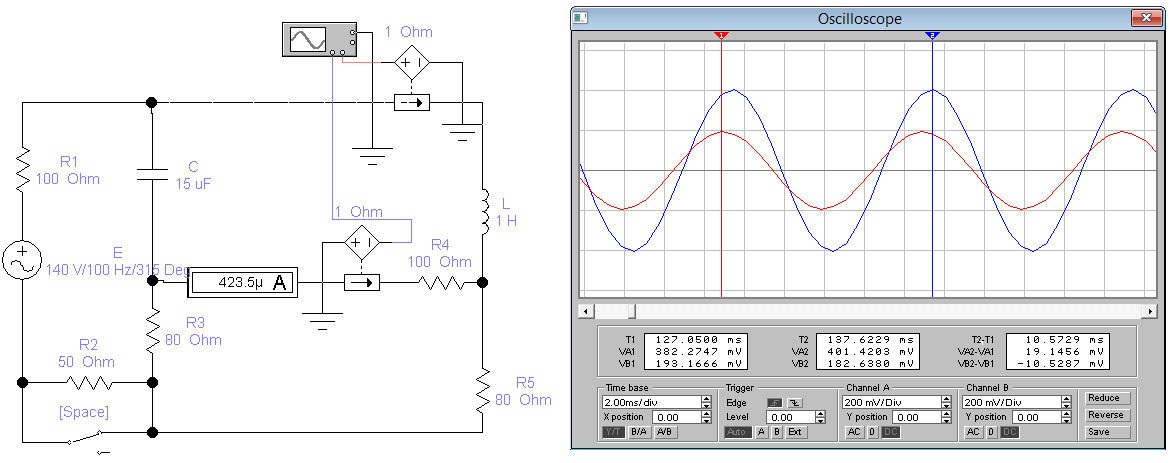
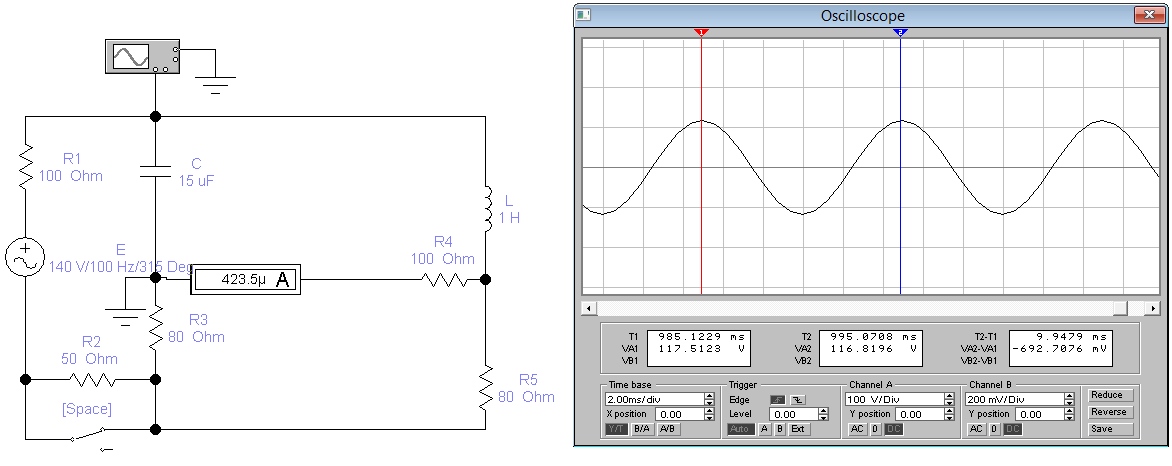
Вывод: в результате проведенной работы методом контурных токов для комплексных амплитуд были определены токи во всех ветвях схемы и напряжения на всех элементах; построены векторные диаграммы токов в цепи и напряжений внешнего контура; построены синусоидальные графики. В результате чего решение, отраженное в MathCAD совпадает с полученным решением в Electronics Workbench.

Задание 3 Расчет переходного процесса в цепи второго порядка

В цепи действует постоянная э.д.с. e(t)=E.

Рассчитать классическим и операторным методами переходной процесс после коммутации, найти зависимости в виде функций времени:

• 
  u_C(t) – (напряжение на конденсаторе);
  
• 
  i_L(t) – (ток в ветви с катушкой индуктивности);
  
• 
  i_R(t) – (ток в резисторе R, отмеченный в схеме).
  

Интервал времени, в пределах которого нужно выполнить построение кривых, выбирается таким, чтобы отклонение тока и напряжения от установившихся значений не превышало 3%.

Собранная схема с помощью Electronics Workbench:

---

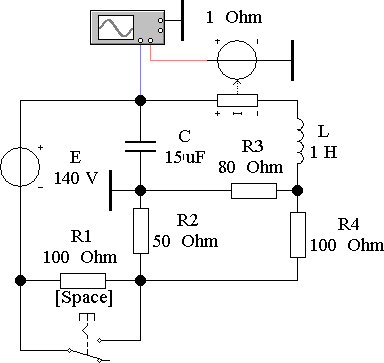
Из решения задания №1 имеем

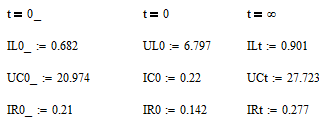
3.1 Расчет переходного процесса классическим методом

Определим входное операторное сопротивление:



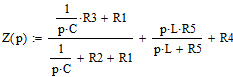
Приравняв это уравнение к нулю и после подстановки численных значений параметров, получим корни характеристического уравнения:



Таким образом, свободную составляющую для тока в катушке, можно записать в виде:



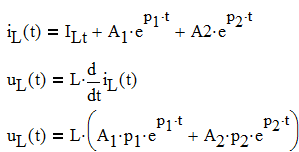
Аналогичное уравнение можно написать для напряжения на емкости:



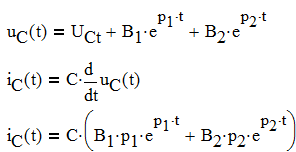
Постоянные интегрирования в этих уравнениях определим, используя законы коммутации:

Для тока i_L (t) Для напряжения u_C(t)



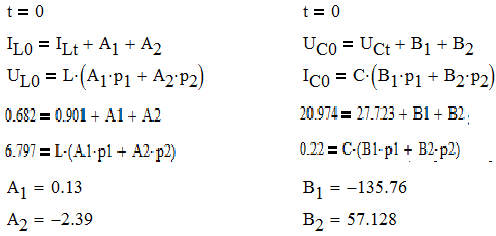
После подстановки найденных значений постоянных интегрирования найдем окончательное значение тока на индуктивности и напряжения на емкости:



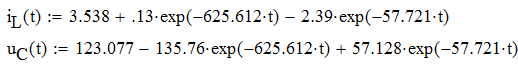
Ток i_R(t) через резистор R₃ найдем по формуле:



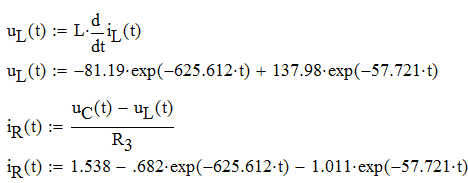
Построим графики изменения тока на индуктивности L, напряжения на емкости С и тока на резисторе R₄:

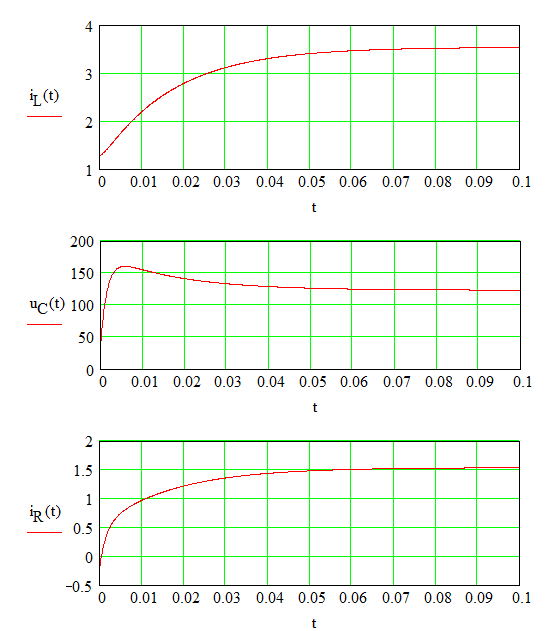
3.2 Расчет переходного процесса операторным методом

Построим операторную схему замещения, которая соответствует схеме после замыкания ключа:

---