Файл: Расчетнографическая работа по дисциплине Оптимизация структуры и технологии работы транспортных систем Проверил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 26
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Статистическая задача. Железнодорожный полигон в терминах транспортной задачи
2 Динамическая задача на основе исходных данных заданного полигона
2.1 Краткие теоретические сведения
2.2 Решение динамической задачи
Для выполнения задания были использованы решения для статистической и динамической задачи.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное государственное образовательное учреждение
высшего образования
«Уральский государственный университет путей сообщения»
(ФГБОУ ВО УрГУПС)
Кафедра «Управление эксплуатационной работой»
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
по дисциплине
«Оптимизация структуры и технологии работы транспортных систем»
Проверил: Выполнил:
доцент кафедры студент группы Тпл- 528(з)
В. Ю. Пермикин Макаров А.В
Екатеринбург
2023
Оглавление
ВВЕДЕНИЕ 2
1 Статистическая задача. Железнодорожный полигон в терминах транспортной задачи 4
1.1Краткие теоретические сведения 4
1.2Решение статистической задачи 6
2 Динамическая задача на основе исходных данных заданного полигона 9
2.1 Краткие теоретические сведения 9
2.2 Решение динамической задачи 9
Для выполнения задания были использованы решения для статистической и динамической задачи. 19
ВВЕДЕНИЕ
В данной работе преследуем цель — конкретизировать, углубить и закрепить знания в профессиональной деятельности в соответствии с компетенциями ОПК-1 и ОПК-2: способностью решать стандартные задачи профессиональной деятельности на основе информационной и библиографической культуры с применением информационно-коммуникационных технологий и с учетом основных требований информационной безопасности, способностью понимать научные основы технологических процессов в области технологии, организации, планирования и управления технической и коммерческой эксплуатацией транспортных систем.
Выполнение работы направлено на закрепление полученных знаний по конкретным темам, развитие самостоятельного мышления, приобретение навыков выделять главное, обобщать, делать выводы.
После выполнения данной работы мы будем уметь:
– проводить обследование для сбора информации о структуре и технологии работы транспортных систем
;
– применять данные обследования о работе транспортных систем при разработке транспортных задач на компьютере;
– формировать варианты транспортных задач для конкретных полигонов транспортной сети;
– применять результаты расчетов динамических транспортных задачи при разработке оптимальных транспортных процессов.
Изучение материала позволяет получить систематизированные знания о способах применения различных постановок транспортных задач для решения вопросов управления грузопотоками и вагонопотоками на больших полигонах транспортной сети.
1 Статистическая задача. Железнодорожный полигон в терминах транспортной задачи
В соответствии с выданным преподавателем схемой и характеристикой железнодорожного полигона выделим для него элементы транспортной задачи – переменные, ограничения, целевую функцию. Для станций полигона укажем их роль: поставщик, потребитель или транзитная станция для каждого вида груза. Сформируем матрицу статической транспортной задачи.
-
Краткие теоретические сведения
Классическая транспортная задача – задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов производства (станций отправления) в пункты потребления (станции назначения).
Транспортная задача формулируется следующим образом. Имеется m пунктов производства (А1,…, Аm) однородного продукта или взаимозаменяемых продуктов и n пунктов потребления (В1,…, Вn). Заданы объемы производства аi каждого пункта производства и размеры спроса bjкаждого пункта потребления в одних и тех же единицах (в штуках, тоннах, вагонах или других единицах измерения). Известны также транспортные издержки Сij(расходы), связанные с перевозкой единицы продукта из пункта Аi в пункт Bj. В термин «транспортные издержки» не всегда вкладывается его непосредственный экономический смысл. Транспортные издержки здесь –условное понятие, которое в различных задачах может означать себестоимость, расстояние, тариф, время, расход топлива и т.д. В транспортной задаче требуется составить план перевозок, обеспечивающий наиболее экономным путем (т.е. при минимальных общих транспортных издержках) удовлетворение спроса всех пунктов потребления за счет реализации всего продукта, произведенного всеми пунктами производства.
Приведенная формулировка транспортной задачи называется замкнутой транспортной моделью. Единственным условием разрешимости замкнутой транспортной задачи является равенство суммарного спроса
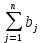 суммарному производству
суммарному производству 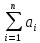 .
. Пусть xij – количество единиц продукта, поставленное из пункта Ai в пункт Bj. Необходимо составить наиболее экономный план перевозок, минимизирующий функцию:
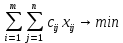 (1)
(1)при условиях: полного удовлетворения спроса потребителей
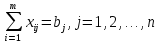 (2)
(2)и обеспечения вывоза всего производственного продукта
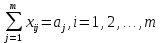 (3)
(3)при этом естественно считать объемы перевозок неотрицательными числами
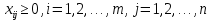 (4)
(4)Задачу будем называть статической транспортной задачей (СТЗ). СТЗ предполагает неизменность во времени программ работы поставщиков и потребителей, т. е. найденное решение задачи «постоянно» на всем интервале времени.
-
Решение статистической задачи
Имеется определенное число поставщиков и потребителей однородной продукции (рис. 1.1). Известны объемы производства и потребления, а также сроки доставки продукции по каждому варианту перевозки.
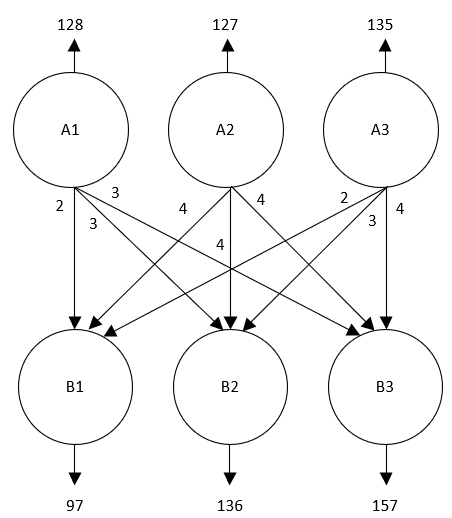
Рисунок 1.1 — Схема дуг статистической транспортной задачи
Для решения задачи запишем целевую функцию:
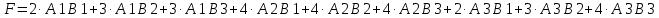
Составим матрицу ограничений (табл. 1.1).
Таблица 1.1 — Матрица ограничений
| Переменные Ограничения | A1B1 | A1B2 | A1B3 | A2B1 | A2B2 | A2B3 | A3B1 | A3B2 | A3B3 | Значения ограничения |
| A1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 128 |
| A2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 127 |
| A3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 135 |
| B1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 97 |
| B2 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 136 |
| B3 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 157 |
| затраты | 2 | 3 | 3 | 4 | 4 | 4 | 2 | 3 | 4 | |
На основе матрицы ограничений запишем уравнения ограничений:
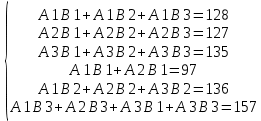
Условиязадачи:
NAME task1
ROWS
N F
E A1
E A2
E A3
E B1
E B2
E B3
COLUMNS
A1B1 F 2
A1B1 A1 1
A1B1 B1 1
A1B2 F 3
A1B2 A1 1
A1B2 B2 1
A1B3 F 3
A1B3 A1 1
A1B3 B3 1
A2B1 F 4
A2B1 A2 1
A2B1 B1 1
A2B2 F 4
A2B2 A2 1
A2B2 B2 1
A2B3 F 4
A2B3 A2 1
A2B3 B3 1
A3B1 F 2
A3B1 A3 1
A3B1 B3 1
A3B2 F 3
A3B2 A3 1
A3B2 B2 1
A3B3 F 4
A3B3 A3 1
A3B3 B3 1
RHS
RHS1 A1 128
RHS1 A2 127
RHS1 A3 135
RHS1 B1 97
RHS1 B2 136
RHS1 B3 157
ENDATA
Результат:
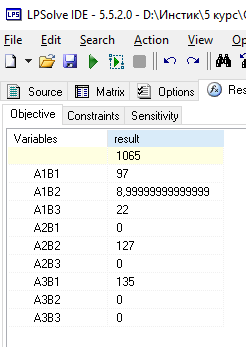
2 Динамическая задача на основе исходных данных заданного полигона
2.1 Краткие теоретические сведения
Использование статической транспортной задачи для оптимизации железнодорожных транспортных систем представляется не эффективным из-за несоответствия исходных посылок транспортной задачи в статической постановке и динамической сущности процессов в адаптивных системах. Из-за неритмичности работы поставщиков и потребителей потоки в системе нестабильны и оптимумом объективно является некоторый динамический процесс с перестраиваемой структурой потоков. Возникает проблема хранения запасов и соответственно учета затрат на это. В условиях неравномерности для обеспечения программ потребителей не всегда выбираются самые дешевые перевозки, так как поставки могут не успевать к нужному моменту времени. Кроме того, в реальных условиях изменение режима перевозок, как правило, связано с теми или иными расходами. Все сказанное обусловило необходимость использования такого варианта транспортной задачи, который бы позволял оптимизировать процессы перевозки в динамике. В описываемом режиме функционирования и при заданных программах поставщиков и потребителей оптимизация перевозок рассматривается как задача минимизации функционала транспортных расходов и суммарных расходов на хранение.
2.2 Решение динамической задачи
Используя исходные данные рисунка 1, рассмотрим динамический процесс, длительностью 10 суток.
Вначале начертим схему дуг в динамическом процессе. По горизонтали размещаем временную шкалу и изображаем состояние поставщиков А1, А2 и А3 и потребителей В1, В2 и В3 в различные моменты времени. Указываем объемы производства и потребления в каждый конкретный момент времени (рисунок 2.1). В целях экономии места и времени начертим временную шкалу для поставщика А1 и потребителя В1, т.к. остальные дуги рисуются идентично по используемой логике.
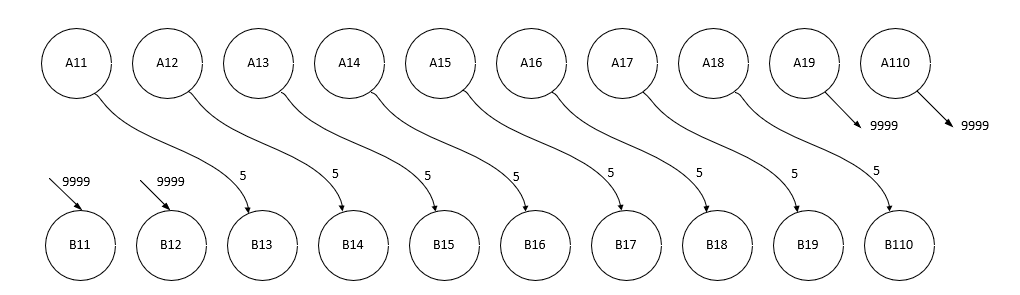
Рисунок 2.1 — Производство и потребление в динамическом процессе, а также дуги перевозок А1В1
По данному рисунку видно, что перевозка А1В1 занимает 2 суток. Соответственно, груз, отправленный от поставщика А1 в первые сутки (А11) прибудет к потребителю В1 на третьи сутки (В13). Аналогичным образом изобразили бы перевозки, исходящие от поставщика А1, А2, А3 в последующие сутки. Стоимость перевозки единицы товара по каждой из указанных дуг — 5.
Не забываем также про «фиктивные» перевозки (перевозки имеют длительность до нескольких суток, возможны ситуации несвоевременного вывоза или подвоза груза). Их стоимость задается во много раз больше — 9999.
Условия задачи:
NAME task2
ROWS
N F
E A11
E A12
E A13
E A14
E A15
E A16
E A17
E A18
E A19
E A110
E A21
E A22
E A23
E A24
E A25
E A26
E A27
E A28
E A29
E A210
E A31
E A32
E A33
E A34
E A35
E A36
E A37
E A38
E A39
E A310
E B11
E B12
E B13
E B14
E B15
E B16
E B17
E B18
E B19
E B110
E B21
E B22
E B23
E B24
E B25
E B26
E B27
E B28
E B29
E B210
E B31
E B32
E B33
E B34
E B35
E B36
E B37
E B38
E B39
E B310
COLUMNS
A11B13 F 5
A11B13 A11 1
A11B13 B13 1
A12B14 F 5
A12B14 A12 1
A12B14 B14 1
A13B15 F 5
A13B15 A13 1
A13B15 B15 1
A14B16 F 5
A14B16 A14 1
A14B16 B16 1
A15B17 F 5
A15B17 A15 1
A15B17 B17 1
A16B18 F 5
A16B18 A16 1
A16B18 B18 1
A17B19 F 5
A17B19 A17 1
A17B19 B19 1
A18B110 F 5
A18B110 A18 1
A18B110 B110 1
A19F F 9999
A19F A19 1
A110F F 9999
A110F A110 1
B11F F 9999
B11F B11 1
B12F F 9999
B12F B12 1
A11B24 F 11
A11B24 A11 1
A11B24 B24 1
A12B25 F 11
A12B25 A12 1
A12B25 B25 1
A13B26 F 11
A13B26 A13 1
A13B26 B26 1
A14B27 F 11
A14B27 A14 1
A14B27 B27 1
A15B28 F 11
A15B28 A15 1
A15B28 B28 1
A16B29 F 11
A16B29 A16 1
A16B29 B29 1
A17B210 F 11
A17B210 A17 1
A17B210 B210 1
A18F F 9999
A18F A18 1
B21F F 9999
B21F B21 1
B22F F 9999
B22F B22 1
B23F F 9999
B23F B23 1
A11B34 F 6
A11B34 A11 1
A11B34 B34 1
A12B35 F 6
A12B35 A12 1
A12B35 B35 1
A13B36 F 6
A13B36 A13 1
A13B36 B36 1
A14B37 F 6
A14B37 A14 1
A14B37 B37 1
A15B38 F 6
A15B38 A15 1
A15B38 B38 1
A16B39 F 6
A16B39 A16 1
A16B39 B39 1
A17B310 F 6
A17B310 A17 1
A17B310 B310 1
B31F F 9999
B31F B31 1
B32F F 9999
B32F B32 1
B33F F 9999
B33F B33 1
A21B15 F 18
A21B15 A21 1
A21B15 B15 1
A22B16 F 18
A22B16 A22 1
A22B16 B16 1
A23B17 F 18
A23B17 A23 1
A23B17 B17 1
A24B18 F 18
A24B18 A24 1
A24B18 B18 1
A25B19 F 18
A25B19 A25 1
A25B19 B19 1
A26B110 F 18
A26B110 A26 1
A26B110 B110 1
A27F F 9999
A27F A27 1
A28F F 9999
A28F A28 1
A29F F 9999
A29F A29 1
A210F F 9999
A210F A210 1
