Файл: Анализ конструктивных особенностей станка модели.doc

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО «КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»


Кафедра «Технология машиностроения, металлорежущие станки и

инструменты»

КУРСОВАЯ РАБОТА

по дисциплине «Теория автоматического управления»

Тема: «Анализ конструктивных особенностей станка модели»

Вариант №5

Выполнил: Паньков Дмитрий Александрович

Студент группы: ИТЗ-30320С

№ зачетной книжки: 132010105

Проверил: Иванова И.А.
Курган 2022

Содержание

Введение

Теория автоматического управления (ТАУ) является одной из наиболее важных общетехнических дисциплин, и ее изучение опирается на ряд фундаментальных общеобразовательных и общетехнических дисциплин – математики, информатики, общей электротехники и электроники и т.д.

Целью настоящей курсовой работы является самостоятельное закрепление теоретических знаний по непрерывным линейным системам автоматического управления, полученных на лекциях, практических занятиях и лабораторных работах. Курсовая работа предусматривает самостоятельное выполнение синтеза и анализа следящей САУ. Синтез производится с помощью ЛАЧХ и ЛФЧХ.

Система интегрированного программирования MathCad является хорошим инструментальным средством для решения задач ТАУ. Основы пользования пакетом изучались в курсе «Спец. Главы информатики». При решении задач по курсу ТАУ необходимо знать и использовать дополнительные возможности пакета, как формирование функций из отрезков прямых линий, определение корней линейных алгебраических уравнений, решение трансцендентных уравнений, нанесение на график логарифмической шкалы, интерполяция и математическая регрессия для данных, представленных в виде векторов.

Приобретенные навыки приемов и методов, применяемых при анализе и синтезе систем автоматического управления, будут использованы в изучении дисциплин «Автоматизированный электропривод», «Моделирование систем».

Исходные данные

---

Структурная схема:



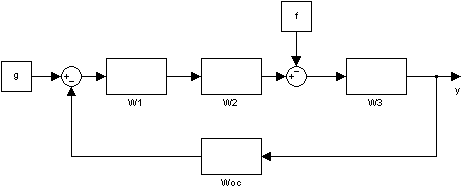
Рисунок 1 – Структурная схема системы
ПФ звеньев и их параметры:

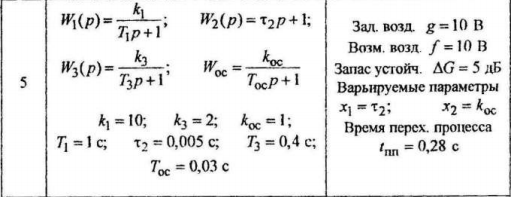
Задание на курсовую работу:

1. Определить типовые звенья, входящие в структуру САУ.

2 Определить передаточные функции САУ и ее характеристический полином.

3. По критерию устойчивости Гурвица определить устойчивость САУ, рассчитать граничное значение коэффициента передачи разомкнутой цепи и построить область устойчивости САУ относительно варьируемых параметров Х1 и Х2.

4. Построить статические и внешние характеристики для заданной САУ и для САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде ΔG. Рассчитать статизм для обоих вариантов САУ и сравнить полученные результаты.

5. Для САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде ΔG, рассчитать асимптотическую и точную ЛАЧХ, точную логарифмическую фазовую частотную характеристику и определить запас устойчивости по фазе Δφ.

6. Для замкнутой САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде ΔG, рассчитать амплитудную (АЧХ) и вещественную (ВЧХ) частотные характеристики и определить по ним показатели качества регулирования.

7. Для замкнутой САУ, у которой значение параметра Х2 выбрано в соответствии с заданным запасом устойчивости по амплитуде ΔG, рассчитать переходные характеристики по задающему g и возмущающему f воздействиями, определить по ним показатели качества регулирования и сравнить результаты с ранее полученными.

8. Исходя из заданного времени переходного процесса tпп и перерегулирования δ=25% провести синтез последовательного корректирующего устройства и рассчитать переходную характеристику скорректированной САУ по задающему воздействию. Определить показатели качества регулирования для этой САУ и сравнить их с ранее рассчитанными.

Задание 1

В состав системы входят следующие звенья:
– апериодическое (инерционное) звено 1 порядка

---

– форсирующее звено

– апериодическое (инерционное) звено 1 порядка

– апериодическое (инерционное) звено 1 порядка

Задание 2

С помощью MathCad рассчитываем ПФ по задающему и возмущающему воздействиям:

При расчёте ПФ по входу g полагаем, что возмущающее воздействие отсутствует:



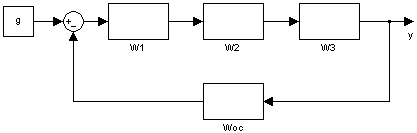
Рисунок 2 – Расчёт ПФ системы по входу g

ПФ отдельных звеньев:



ПФ разомкнутой системы по входу g рассчитывается как произведение ПФ всех звеньев, включённых в замкнутый контур:



ПФ замкнутой системы по входу g:


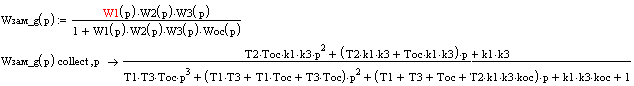
Теперь рассчитаем ПФ по входу f: При расчёте ПФ по входу f полагаем, что задающее воздействие отсутствует:



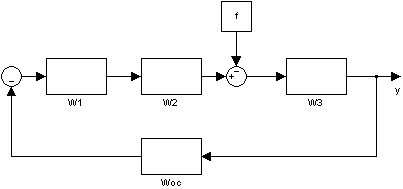
Рисунок 3 – Расчёт ПФ системы по входу f

ПФ разомкнутой системы по входу f:


ПФ замкнутой системы по входу f:


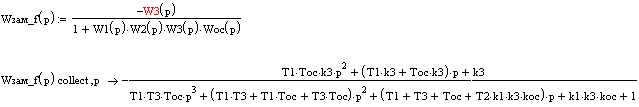
Знаменатели рассчитанных ПФ по входам g и f совпадают, следовательно, расчёты произведены верно.

Задание 3

Рассчитаем устойчивость замкнутой системы алгебраическим критерием Гурвица:
Выделяем характеристический полином замкнутой системы – знаменатель ПФ:


Подставляем числовые коэффициенты:


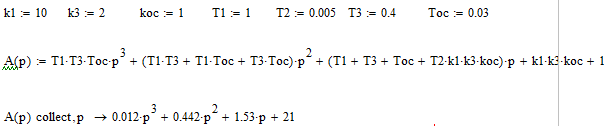
По необходимому условию Гурвица, все коэффициенты характеристического полинома должны быть положительными. Данное условие выполняется.

---

По достаточному условию Гурвица, определители всех порядков матрицы Гурвица должны быть положительными.

Формируем матрицу Гурвица:


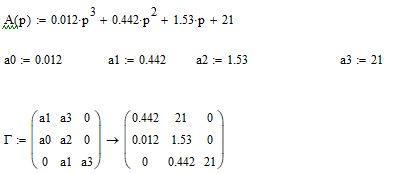
Рассчитываем определители матрицы Гурвица:



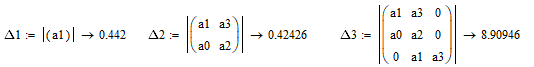
Определители всех 3 порядков матрицы Гурвица положительные, следовательно, исходная система в замкнутом состоянии будет устойчива.

Найдём граничное условие коэффициента передачи, при котором система будет находиться на границе устойчивости. Полагаем общий коэффициент передачи, равным произвдению коэффициентов усиления отдельных звеньев:
Формируем матрицу Гурвица:



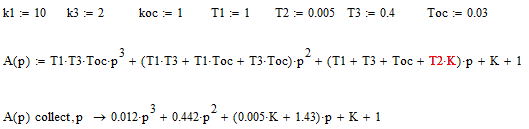
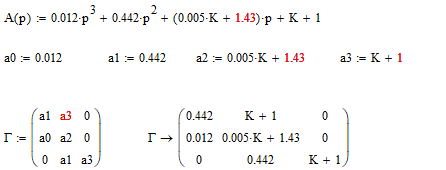
Находим определитель 3 порядка:


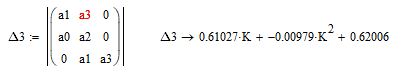
Найдём решение 3 определителя матрицы Гурвица:


Система будет устойчива при -1 < K < 63,336. Отметим, что значение -1 соответствует апериодической границе устойчивости, а корень 63,336 соответствует колебательной границе устойчивости.

Построим границу устойчивости в вариации параметров Х1, Х2.

По условию, в качестве параметра Х1 используется постоянная времени Т₂; в качестве Х2 используется коэффициент усиления k_oc.

Тогда


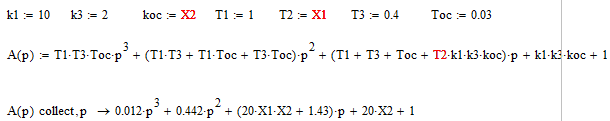
Формируем матрицу Гурвица:


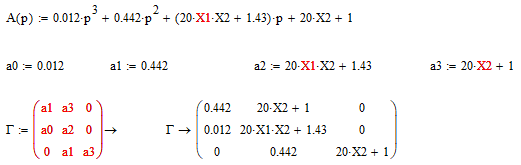
Рассчитываем определители:


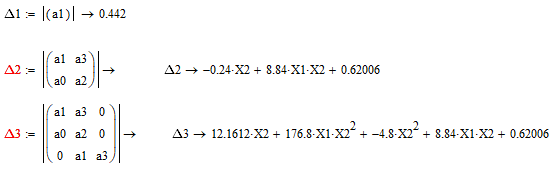
Найдём решение Х1 для 2 и 3 определителей матрицы Гурвица относительно Х2:



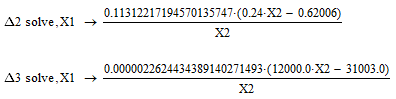
Построим зависимость Х1(Х2). Поскольку, по необходимому условию Гурвица, все коэффициенты должны быть положительными, выбираем только 1 четверть:




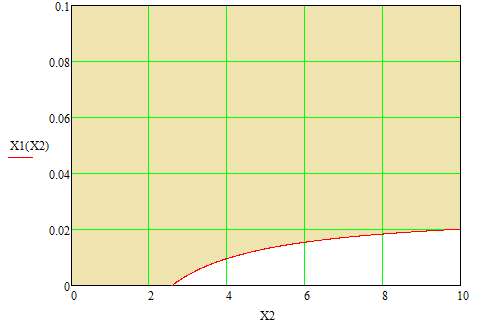
Рисунок 4 – Область устойчивости параметров Х1 и Х2

---

На рисунке 4 представлена граница устойчивости параметров Х1 и Х2. Красная линия соответствуют колебательной границе устойчивости. При выборе пары чисел Х1 и Х2, лежащих на данной линии, замкнутая система будет находиться на колебательной границе устойчивости. При выборе пары чисел Х1 и Х2, лежащих правее/ниже данной линии, замкнутая система будет неустойчива. При выборе пары чисел Х1 и Х2, лежащих левее данной линии (закрашенная область), замкнутая система будет устойчива.

Задание 4

Ранее мы определили, что критический коэффициент усиления разомкнутой системы: К ≈ 63,336.

Подставляя исходные коэффициенты k₁ и k₃, определим критический коэффициент X₂ = k_ос:



Далее находим новое значение k_ос, при котором будет обеспечиваться требуемый запас устойчивости ΔG = 5 дБ:


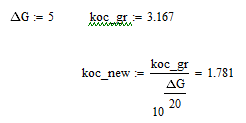
Внешняя характеристика САУ при изменении возмущающего воздействия от нуля до fm рассчитывается по передаточным функциям замкнутой САУ при p=0, то есть по формуле


Найдём значения Wzg(0) и Wzf(0):



Строим внешние характеристики для исходной (y(f)) и скорректированной (y1(f)) систем:



Уточнение задающего воздействия, обеспечивающего одинаковую выходную величину для обеих САУ при  = 0



Строим характеристики:




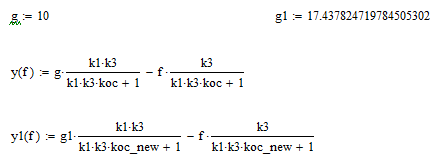
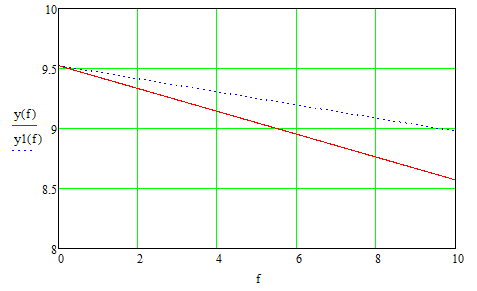
Рисунок 5 – Внешние характеристики
Легко видеть, что при новом значении k_ос внешняя характеристика САУ менее жесткая (то есть при одном и том же значении f наблюдается меньшее отклонение выходной величины от заданного значения).
Значение выходной величины при f = 0:



Значения выходной величины при f = 10:

---