ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 29
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Отклонения выходной величины от заданного значения при f = fm:
Статизм внешних характеристик:
Задание 5
Асимптотическая ЛАЧХ разомкнутой цепи САУ строится путем суммирования асимптотических ЛАЧХ ее отдельных звеньев:

Уравнения асимптотических ЛАЧХ отдельных звеньев:

Асимптотическая ЛАЧХ разомкнутой цепи САУ строится путем суммирования асимптотических ЛАЧХ ее звеньев:
Реальная ЛАЧХ системы рассчитывается по формуле:
Построим реальную и асимптотическую ЛАЧХ на одном графике. Отметим, что на частотах сопряжения между асимптотической и действительной ЛАЧХ возникает погрешность ≈ 3 дБ.

Рисунок 6 – Асимптотическая и реальная ЛАЧХ системы
Уравнение точной ЛФЧХ системы можно представить как сумму точных ЛФЧХ отдельных звеньев:
Построим точную ЛФЧХ:

Рисунок 7 – ЛФЧХ системы
Определим запасы устойчивости по амплитуде и фазе:
На частоте среза ЛАЧХ значение ЛФЧХ составляет: φ(ω) = –170.956º. Следовательно, запас устойчивости по фазе составит: Δφ = 180º–170.956º = 9.044º.
На критической частоте ЛФЧХ значение ЛАЧХ составляет –5 дБ. Следовательно, запас устойчивости по амплитуде ΔL составляет 5 дБ, что соответствует заданному условию.
Задание 6
Построим АЧХ и ВЧХ замкнутой системы:
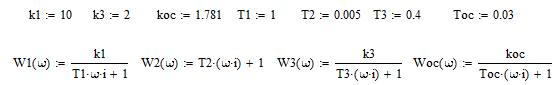
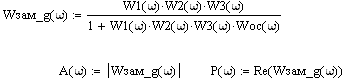

Рисунок 8 – ВЧХ и АЧХ замкнутой системы
По ВЧХ определим перерегулирование:
Перерегулирование не будет превышать 429.8%.
По АЧХ рассчитаем показатель колебательности:
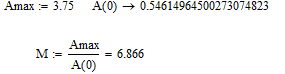
Задание 7
ПФ замкнутой системы по задающему воздействию:

Уравнение переходной характеристики по задающему воздействию:
Найдём установившееся значение переходной характеристики и границы 5%-ого коридора:
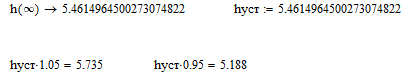

Рисунок 9 – Переходная характеристика замкнутой системы по задающему воздействию
По переходной характеристике определяем показатели переходного процесса:
Длительность переходного процесса tпп = 4,25 с
Максимальное значение выходной величины: hmax = 9,8
Перерегулирование:
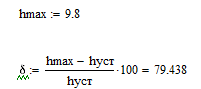
Переходная характеристика по возмущающему воздействию:


Рисунок 10 – Переходная характеристика замкнутой системы по возмущающему воздействию
Задание 8
Синтез последовательного корректирующего устройства наиболее просто провести по логарифмическим частотным характеристикам.
Асимптотическая ЛАЧХ исходной системы построена в задании 5:

Рисунок 11 – Исходная асимптотическая ЛАЧХ
При построении желаемой ЛАЧХ выделяют 3 участка.
Низкочастотная область строится исходя из требований к точности. Поскольку в нашем случае требования к точности не указаны, сопрягаем низкочастотный участок желаемой ЛАЧХ с низкочастотным участком исходной располагаемой ЛАЧХ.
Среднечастотный участок желаемой ЛАЧХ строится исходя из требований
переходного процесса с использованием номограмм Солодовникова:

а) б)
Рисунок 12 – Номограммы Солодовникова
По условию, перерегулирование σ не должно превышать 25%. По номограмме Солодовникова (а) определяем формулу для зависимости времени регулирования tp и частоты среза ωср:

По номограмме Солодовникова (б) определяем протяжённость среднечастотного участка: ΔL = 20 дБ (в случае надобности, его можно продлить).
Высокочастотный участок желаемой ЛАЧХ проходит параллельно высокочастотному участку располагаемой ЛАЧХ.
Строим желаемую ЛАЧХ:

Рисунок 13 – Построение желаемой ЛАЧХ
ЛАЧХ КУ находится графическим вычитанием исходной ЛАЧХ из желаемой ЛАЧХ:

Рисунок 14 – Построение ЛАЧХ КУ
По ЛАЧХ КУ определяем ПФ корректирующего устройства:
Также обратим внимание, что в контуре обратной связи присутствует апериодическое звено с постоянной времени Тос = 0,03 которое может дать большое перерегулирование.
Для его устранения включим одно из рассчитанных интегродифференцирующих звеньев КУ в контур обратной связи – постоянная времени в числителе которого равна постоянной времени звена Тос, а постоянная времени знаменателя которого имеет минимальное значение: 0,002.
Тогда переходная характеристика:

Строим переходную характеристику замкнутой скорректированной системы:

Рисунок 15 – Переходная характеристика замкнутой скорректированной системы
Перерегулирование отсутствует; есть только положительное отклонение; время регулирования составляет 0,05 c - менее требуемых 0,28 с; следовательно КУ синтезировано верно.
Выводы
Рассчитаны ПФ разомкнутой и замкнутой системы по возмущающему и задающему воздействиям. Выявлен характеристический полином замкнутой системы; произведено исследование устойчивости системы.
Найден граничный коэффициент усиления, при котором система находится на колебательной границе устойчивости; построена область устойчивости для 2 заданных параметров.
Построены статические характеристики системы.
Рассчитаны запасы устойчивости по амплитуде и фазе системы.
По частотным и временным характеристикам определены показатели качества переходного процесса.
Методом ЛАЧХ синтезировано корректирующее устройство, обеспечивающее параметры переходного процесса, предъявляемые в задании. Построена переходная характеристика скорректированной системы. Анализ данной переходной характеристики показал, что требования выполняются, следовательно, синтез КУ произведён верно.
Литература
[1] Иващенко Н. Н. Автоматическое регулирование. Теория и элементы систем. Учебник для вузов. Изд. 4-е, перераб. и доп. М., «Машиностроение», 1978. - 736 с.
[2] Тюкин В.Н. Теория управления. Вологодский государственный технический университет. Часть 1. Обыкновенные линейные системы управления.
[3] Солодовников В.В., Плотников В.Н., Яковлев А.В. Теория автоматического управления техническими системами: Учеб. Пособие. – М.: Изд-во МГТУ, 1993. – 492 с., ил.
4) Теория автоматического управления: учеб. для вузов по спец. «Автоматика и телемеханика». В 2-х ч. 4.1. Теория линейных систем автоматического управления / H.A. Бабаков, [и др.]; под ред.A.A. Воронова.-2-е изд., перераб. и доп. – М.: Высш. шк., 1986. –367 c., ил.
5) Пантелеев, A.B. Теория управления в примерах и задачах [текст]: учеб. пособие / A.B. Пантелеев, A.C. Бортаковский. - М.: Высш. шк., 2003. – 583 c.: ил.





Изм.
Кол.уч
№ док.
Подпись
Дата
Лист
- -
Лист
