Добавлен: 05.05.2024
Просмотров: 48
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное автономное
образовательное учреждение высшего образования
«САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ имени академика С. П. КОРОЛЁВА»
ИНСТИТУТ РАКЕТНО-КОСМИЧЕСКОЙ ТЕХНИКИ
Кафедра космического машиностроения
Курсовая работа по дисциплине
«Конечно-элементное моделирование конструкций»
Выполнил: студент гр. 1404 Белоусова Д.А.
Проверил: доц. Скворцов Ю. В.
Оценка
Дата
Подпись
САМАРА 2019
РЕФЕРАТ
Пояснительная записка 15 с., 10 рисунков, 3 источника.
КОЛЕБАНИЯ, КОНЕЧНО-ЭЛЕМЕНТНАЯ МОДЕЛЬ, МОДАЛЬНЫЙ АНАЛИЗ, НАПРЯЖЕНИЯ, НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ, ПЕРЕМЕЩЕНИЯ, ПЕРИОДИЧЕСКАЯ СИЛА, СОБСТВЕННЫЕ ЧАСТОТЫ.
Объект исследования – балочно-оболочечная конструкция.
Цель работы – выполнение модального и гармонического анализа конструкции.
В результате работы получены величины собственных частот колебаний конструкции, деформированные формы конструкции при собственных колебаниях, максимальные значения перемещений и напряжений в конструкции от действия периодической силы с заданным диапазоном изменения частоты силы.
СОДЕРЖАНИЕ
Введение 5
1 Создание конечно-элементной модели балочно-оболочечной конструкции 6
2 Модальный анализ балочно-оболочечной конструкции 7
3 Определение отклика системы на периодическую силу 10
Заключение 14
Список использованных источников 15
Введение
В данной работе проводятся модальный и гармонический анализы балочно-оболочечной конструкции.
При выполнении модального анализа определяются первые 5 собственных частот конструкции и соответствующие им формы колебаний.
При выполнении гармонического анализа определяется отклик системы на периодическую силу. Ожидается, что наибольшие перемещения и напряжения в конструкции возникнут в случае, когда частота изменения силы достаточно близка или совпадает с одной из собственных частот колебаний конструкции. Такой случай является наиболее опасным при нагружении конструкции, так как в данных условиях возникает резонанс, который может привести к разрушению конструкции.
1 Создание конечно-элементной модели балочно-оболочечной конструкции
Конструкция представляет собой две вертикальные балки, соединенные между собой плоским прямоугольным листом с отверстием в центре. Пластина смоделирована оболочечными конечными элементами (КЭ) четырехугольной формы, балки – балочными КЭ. КЭМ конструкции представлена на рисунке 1.
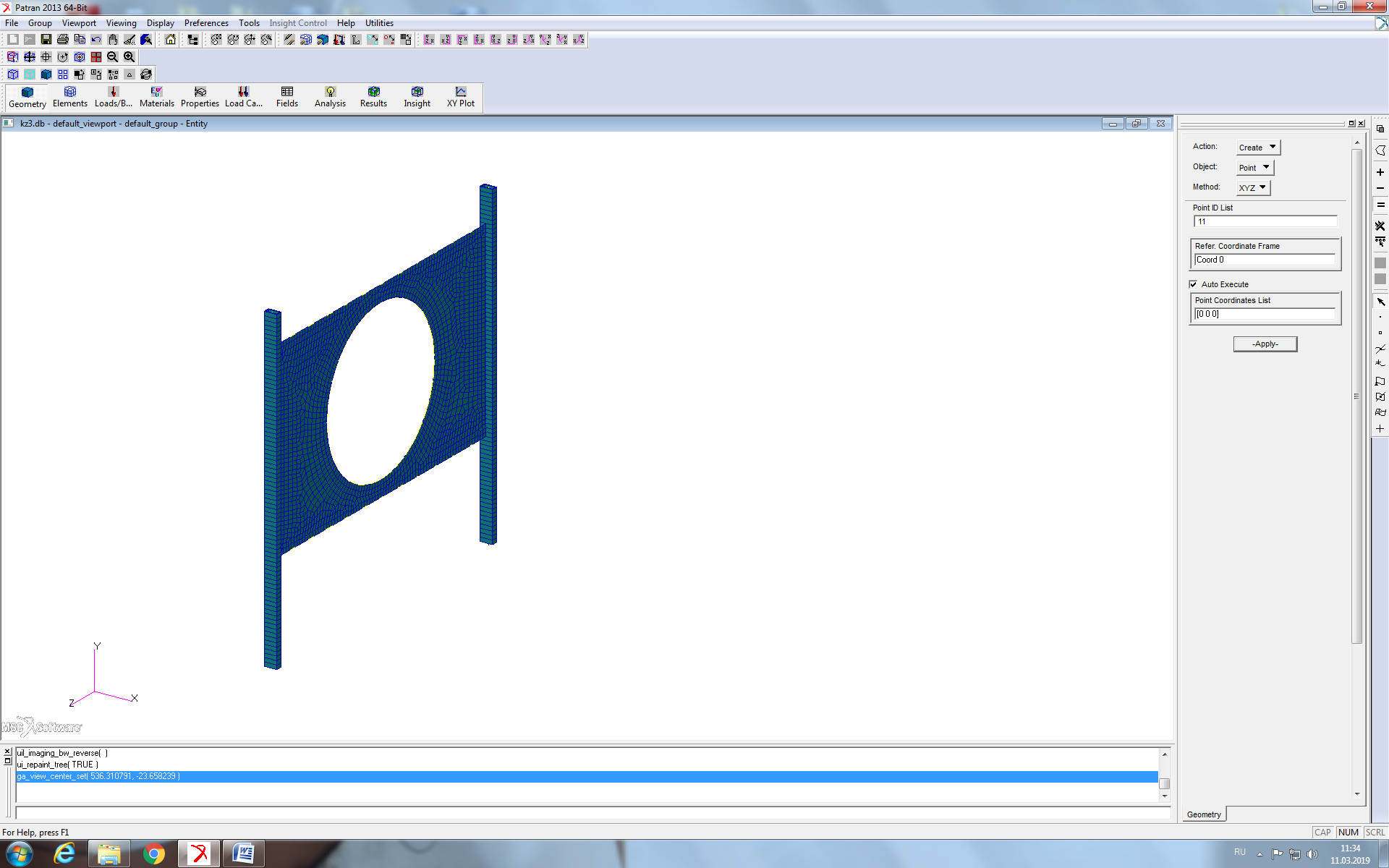
Рисунок 1 - КЭМ балочно-оболочечной конструкции
2 Модальный анализ балочно-оболочечной конструкции
Модальный анализ конструкции был проведен с помощью пакета MSC.Patran/Nastran. Определены первые пять собственных частот конструкции
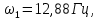
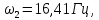
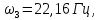
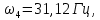
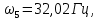
и соответствующие им формы собственных колебаний, которые представлены на рисунках 2-6.
Рисунок 2 - Первая форма собственных колебаний конструкции
Рисунок 3 - Вторая форма собственных колебаний конструкции
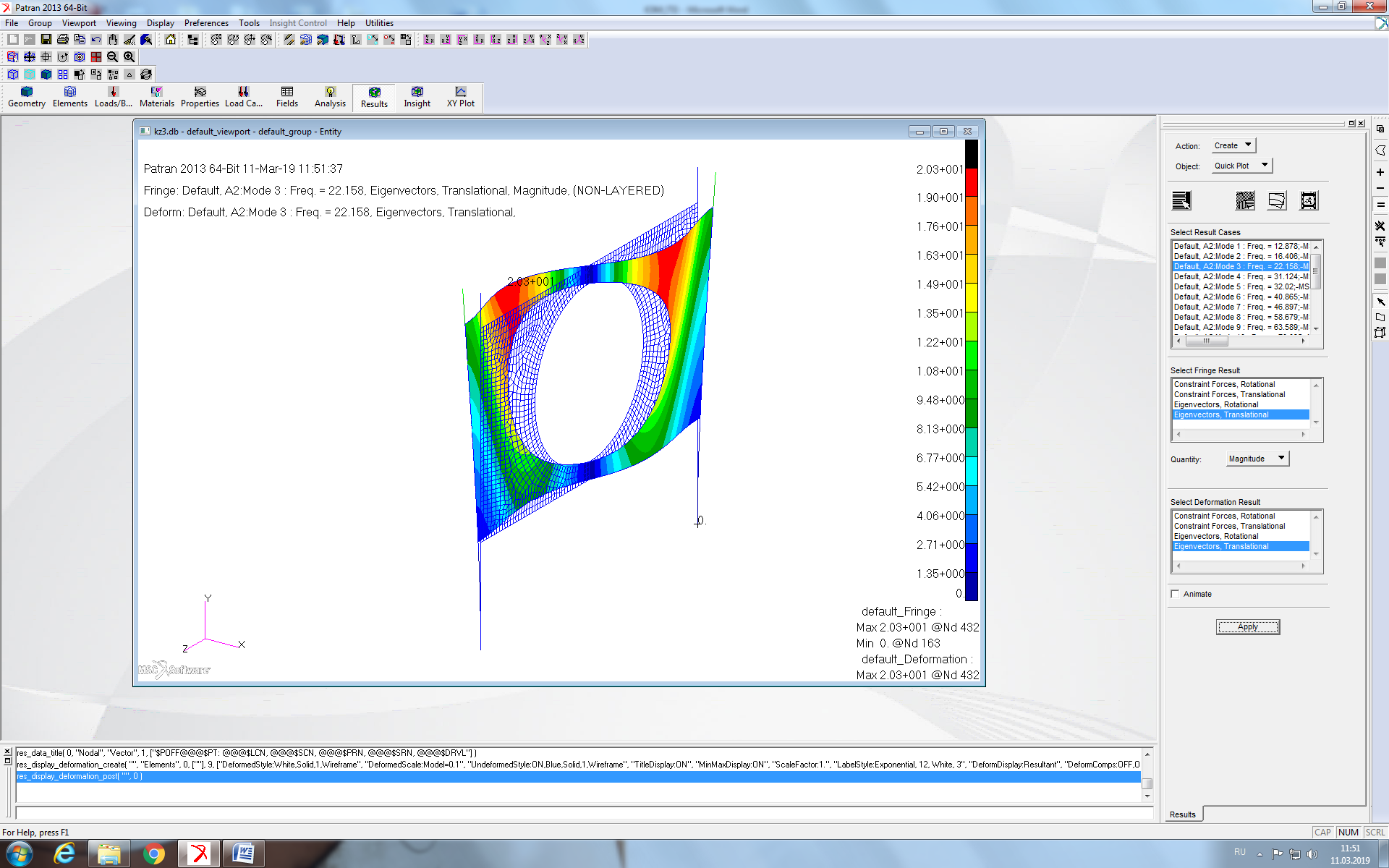
Рисунок 4 - Третья форма собственных колебаний конструкции
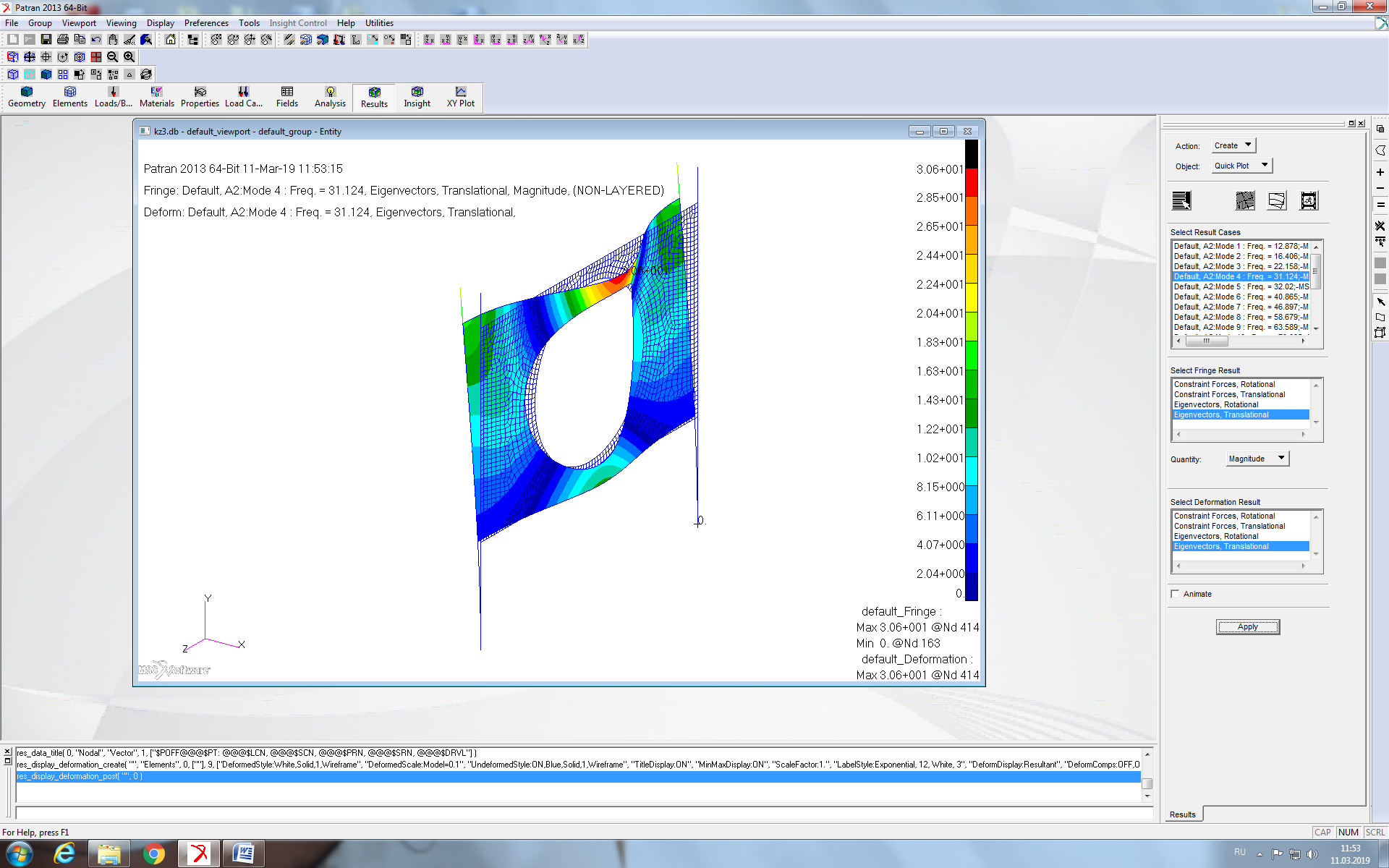
Рисунок 5 - Четвертая форма собственных колебаний конструкции
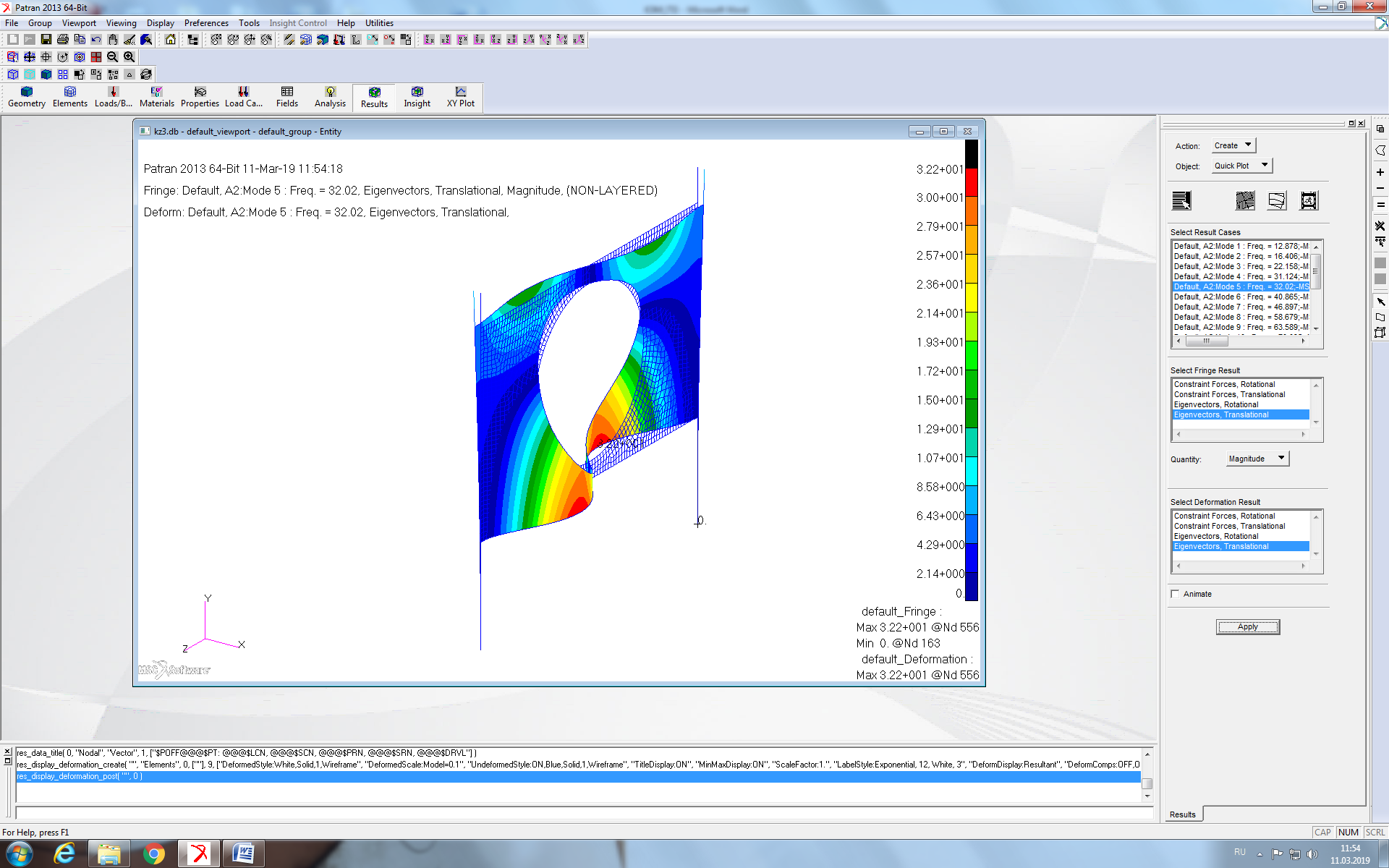
Рисунок 6 - Пятая форма собственных колебаний конструкции
3 Определение отклика системы на периодическую силу
Периодическая сила определяется по закону
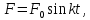
где
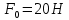 - амплитуда силы,
- амплитуда силы, - частота силы,
- частота силы, - время.
- время.На рисунке 7 показаны приложенные к модели конструкции закрепления и силы.
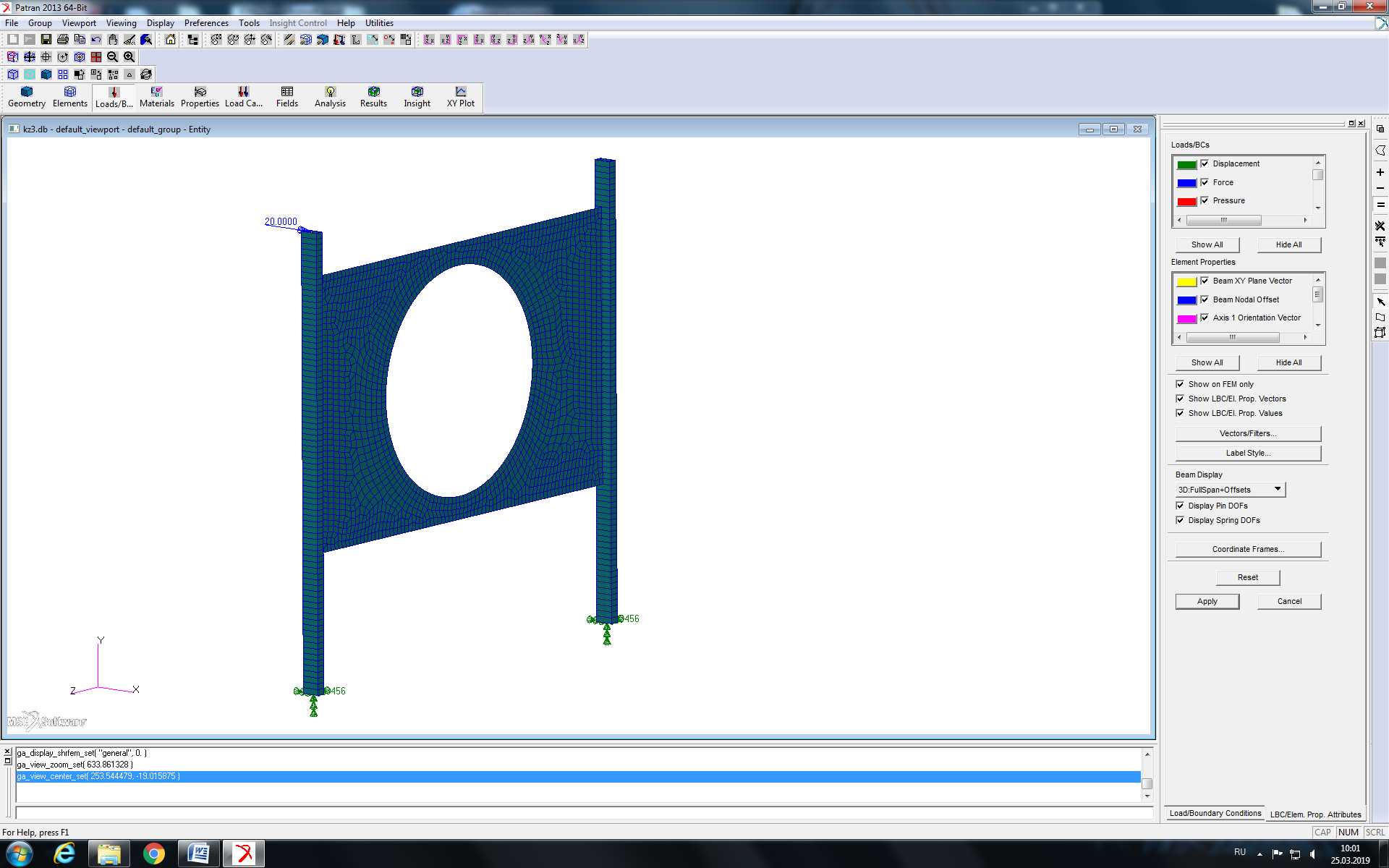
Рисунок 7 - КЭМ конструкции с приложенными закреплениями и нагрузкой
Расчет для определения отклика системы был проведен с помощью пакета MSC.Patran/Nastran. На рисунке 8 представлен график зависимости перемещения точки 1 от частоты приложенной силы (направление перемещения – по нормали к плоскости оболочки).
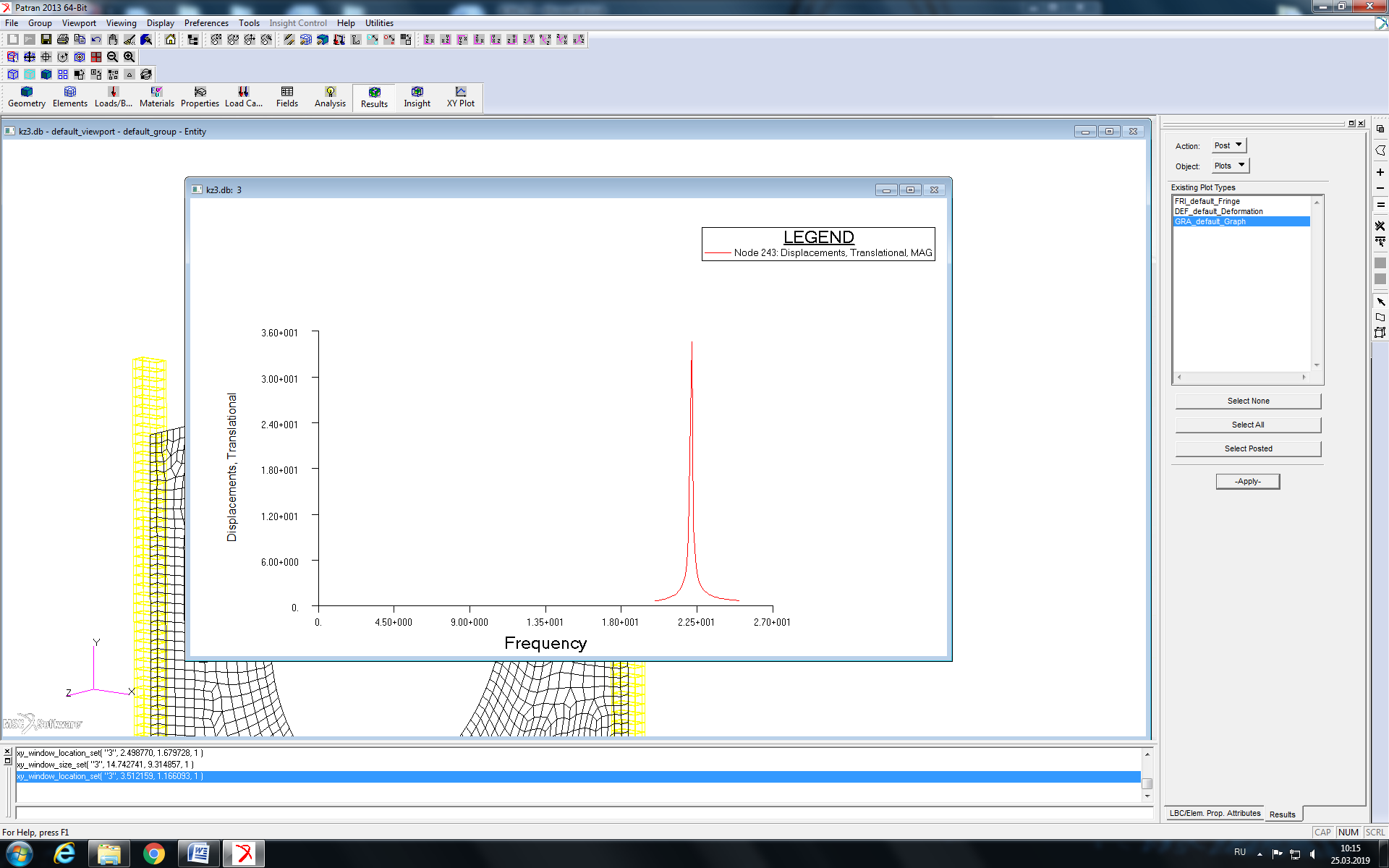
Рисунок 8 - график зависимости перемещения точки 1 от частоты приложенной силы
По данному графику видно, что максимальные перемещения точки реализуются при частоте силы
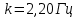 , совпадающей с одной из собственных частот колебаний конструкции, так как при этом значении частоты наступает резонанс.
, совпадающей с одной из собственных частот колебаний конструкции, так как при этом значении частоты наступает резонанс.Для частоты
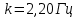 определены точки оболочки с максимальными перемещениями по нормали к плоскости оболочки. Реализуемые перемещения равны 62,3 мм в направлении оси X. Деформированное состояние конструкции при действии силы с заданной частотой показано на рисунке 9. На рисунке 10 показано распределение напряжений по Мизесу в среднем слое оболочки. Максимальное значение напряжений 677 МПа, минимальное 14 МПа.
определены точки оболочки с максимальными перемещениями по нормали к плоскости оболочки. Реализуемые перемещения равны 62,3 мм в направлении оси X. Деформированное состояние конструкции при действии силы с заданной частотой показано на рисунке 9. На рисунке 10 показано распределение напряжений по Мизесу в среднем слое оболочки. Максимальное значение напряжений 677 МПа, минимальное 14 МПа.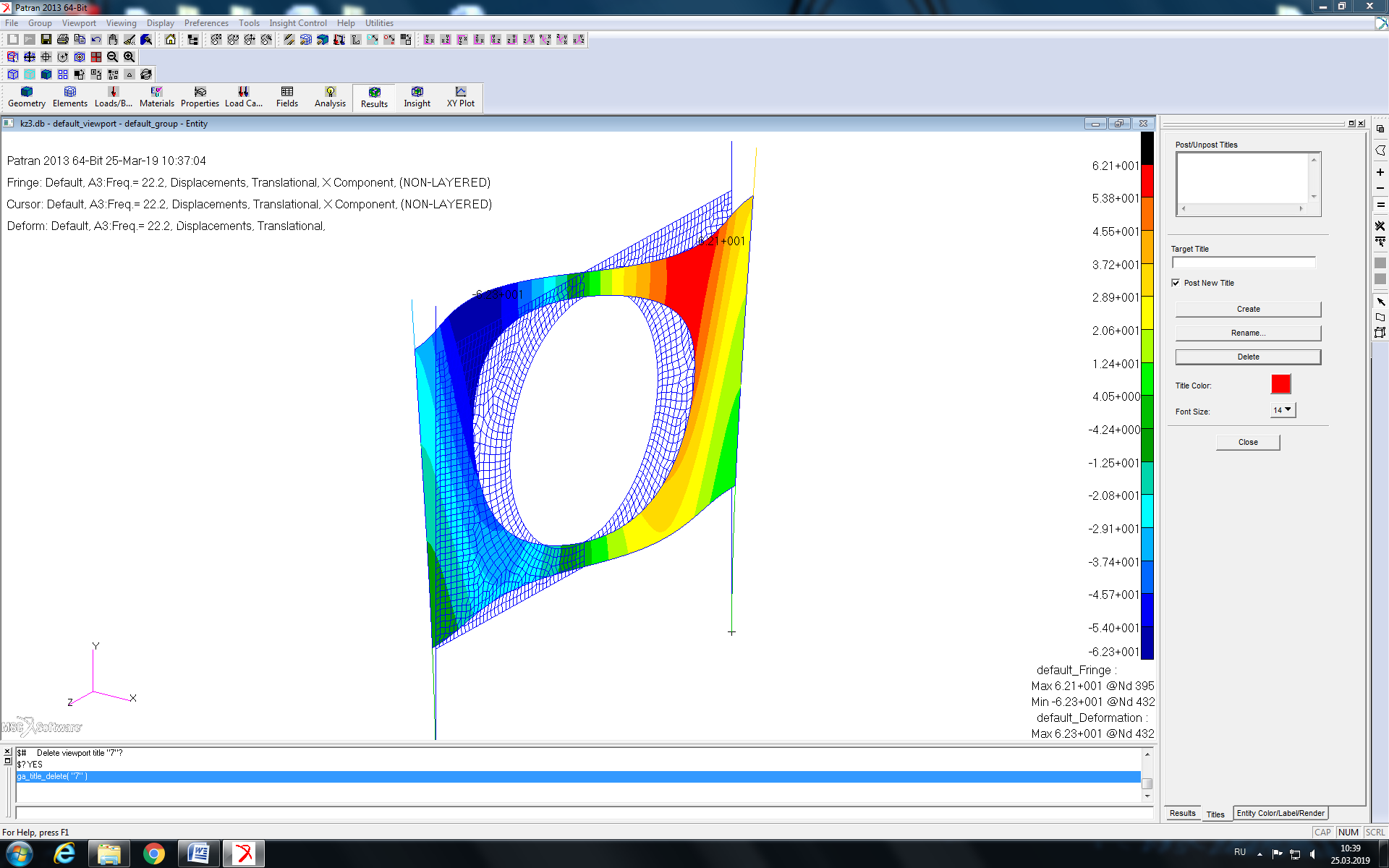
Рисунок 9 - Деформированное состояние конструкции
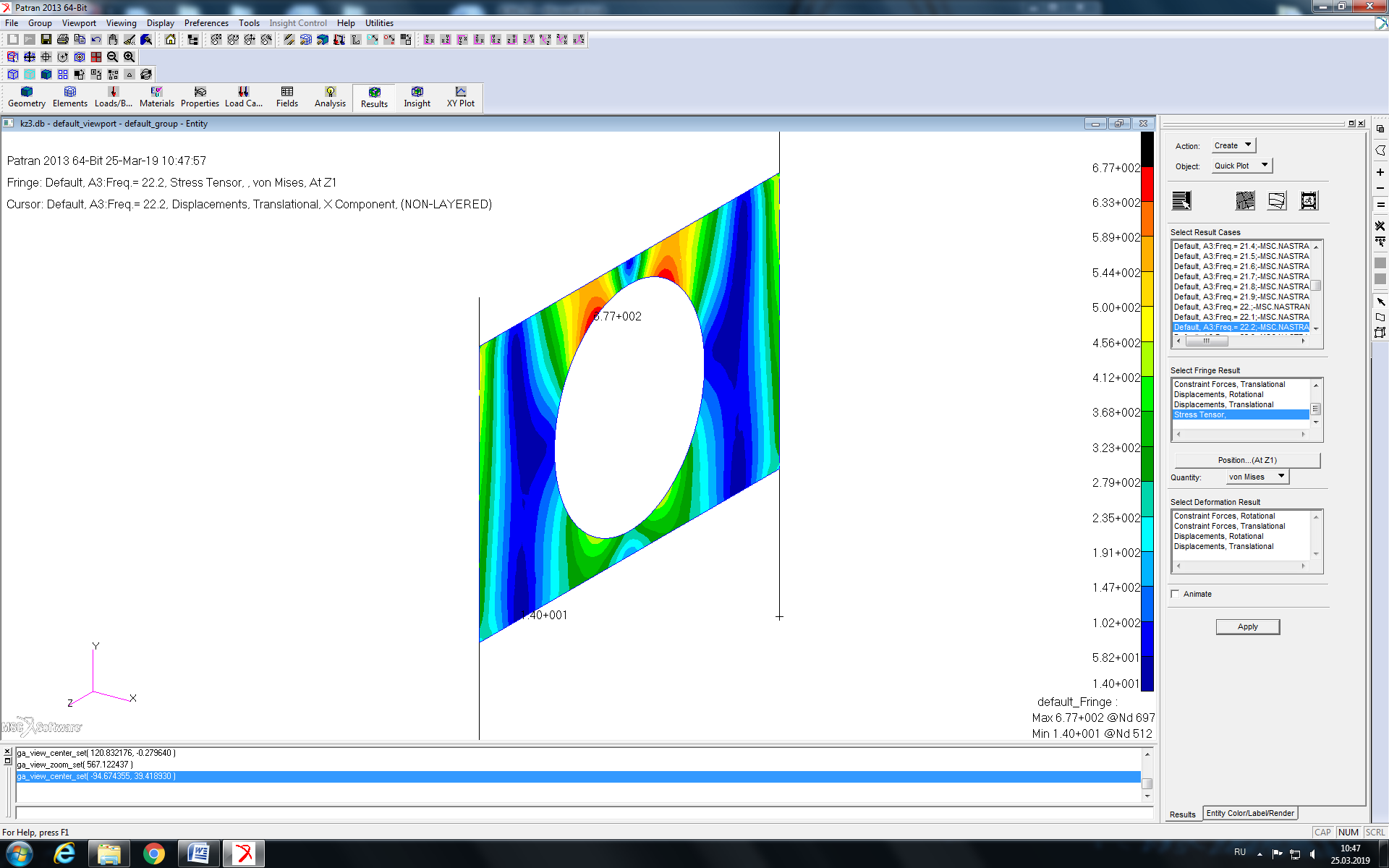
Рисунок 10 - Распределение эквивалентных напряжений по Мизесу в оболочке конструкции
Заключение
В результате работы получены значения первых пяти собственных частот колебаний конструкции и соответствующие им формы колебаний. В результате выполнения гармонического анализа построена зависимость перемещения точки 1 от частоты приложенной силы. Определена частота изменения периодической силы, при которой конструкция имеет наибольший отклик на внешнее воздействие (при данной частоте перемещения точек конструкции максимальны). Для данной частоты определены максимальные перемещения оболочки по нормали к ней. Также в работе представлена картина распределения эквивалентных напряжений по Мизесу в переднем слое оболочки.
Список использованных источников
-
СТО СГАУ 02068410-004-2018. Общие требования к учебным текстовым документам: [Сборник]. – Самара: Самарский университет, 2018. – 29 с. -
Скворцов, Ю. В. Анализ прочности элементов авиационных конструкций с помощью CAE-системы MSC.Patran-Nastran [Электронный ресурс] : интерактив. мультимед. пособие в системе дистанц. обучения «Moodle» / Ю. В. Скворцов, С. В. Глушков; Минобрнауки России, Самар. гос. аэрокосм. ун-т им. С. П. Королева -
Шимкович Д.Г. Расчет конструкций в MSC/NASTRAN for Windows. – М.: ДМК Пресс, 2001. – 448с.
