ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.09.2024
Просмотров: 8
Скачиваний: 0
Лабораторна робота № 8
Тема: Рекурсивні функції
Мета: вивчити способи реалізації алгоритмів з використанням рекурсії.
8.1.1 Короткі теоретичні відомості
Рекурсія - це спосіб організації обчислювального процесу, при якому функція в ході виконання операторів, що входять в неї, звертається сама до себе. Класичним прикладом є обчислення факторіалу n! (n>0)
double Faktorial_R (int n) {
if (n < 2) return 1; // Умова закінчення рекурсії
else
return n* Faktorial_R (n - 1); // Рекурсивне звернення до функції
}
При виконанні правильно організованої рекурсивної функції здійснюється послідовний перехід від поточного рівня організації алгоритму до нижнього рівня, в якому буде отримано рішення задачі (у наведеному прикладі при n < 2), що не вимагає подальшого звернення до функції (не рекурсивне).
При описі алгоритмів використовуємо наступні стандартні фігури блок-схем :

8.1.2 Приклад виконання завдання
Написати програму обчислення факторіалу позитивного числа n, що містить функції користувача з рекурсією і без рекурсії.
8.1.2.1. Реалізація завдання у віконному застосуванні
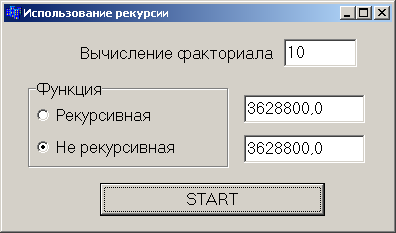
Вид форми і отримані результати представлені на мал. 8.1.1. Компонента Edit1 використовується для введення n, а компоненти Edit2 і Edit3 - для виведення результатів.
Лістинг програми може мати наступний вигляд:
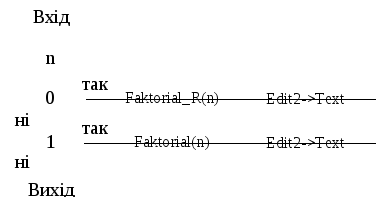
Блок-схема функції-обробника Button1Click представлена на мал. 8.1.2.
. . .
double Faktorial(int);
double Faktorial_R(int);
//--------------------- Кнопка START ---------------------------------------------
void __fastcall TForm1::Button1Click(TObject *Sender)
{
int n = StrToInt(Edit1 ->Text);
switch(RadioGroup1 ->ItemIndex){
case 0:
Edit2 ->Text = FloatToStrF(Faktorial_R(n), ffFixed, 8, 1);
break;
case 1:
Edit3 ->Text = FloatToStrF(Faktorial(n), ffFixed, 8, 1);
break;
}
}
//------------------ Функція без рекурсії ---------------------------------------
double Faktorial(int n) {
double f = 1;
for (int i = 1; i <= n; i++) f *= i;
return f;
}
//------------------- Рекурсивна функція ----------------------------------------
double Faktorial_R(int n) {
if (n < 2) return 1;
else
return n*Faktorial_R(n - 1);
}
Мал. 8.1.1
Мал. 8.1.2
Блок-схеми функцій користувача Faktorial_R і Faktorial представлені на мал. 5.1.3.

Мал. 8.1.3
8.1.2.2. Реалізація завдання в консольному застосуванні
Тексти функцій користувача дивитеся в попередньому прикладі, а лістинг основної функції може мати наступний вигляд:
…
#include <iostream.h>
…
double Faktorial(int);
double Faktorial_R(int);
void main(void)
{
int n, kod;
while(true){ // Нескінченний цикл з виходом по default
cout << "\n\tInput n " ;
cin >> n;
cout << "\n Recurs - 0\n Simple - 1\n Else - Exit" << endl ;
cin >> kod;
switch(kod){
case 0:
cout << "\t Recurs = " << Faktorial_R(n) << endl;
break;
case 1:
cout << "\t Simple = " << Faktorial(n) << endl;
break;
default: return;
}
}
8.2. Індивідуальні завдання
Скласти алгоритм у вигляді блок-схеми, написати і відлагодити поставлене завдання з використанням рекурсивної і звичайної функцій. Порівняти отримані результати.
1. Для заданого цілого десяткового числа N отримати його представлення в p -ічній системі числення (p < 10).
2. У впорядкованому масиві цілих чисел ai (i = 1, ..., n) знайти номер елементу c, що знаходиться в масиві, використовуючи метод двійкового пошуку.
3. Знайти найбільший загальний дільник чисел M і N, використовуючи теорему Ейлера: якщо M ділиться на N, то НЗД (N, M) = N, інакше НЗД(M%N, N).
4. Числа Фібоначчі визначаються таким чином: Fb(0)=0; Fb(1)=1; Fb(n) = Fb(n - 1) + Fb(n - 2). Визначити Fb(n).
5. Знайти значення функції Аккермана A(m, n), яка визначається для усіх ненегативних цілих аргументів m і n таким чином :
A(0, n) = n + 1;
A(m, 0) = A(m - 1, 1); при m > 0;
A(m, n) = A(m - 1, A(m, n - 1)); при m > 0 і n > 0.
6. Знайти методом ділення відрізку навпіл мінімум функції f(x) = 7*sin(2*x) на відрізку [2, 6] із заданою точністю (наприклад, 0.01).
7. Вичислити значення x
=
![]() ,
використовуючи рекурентну формулу xn
=
,
використовуючи рекурентну формулу xn
=
![]() ,
в якості початкового значення
використовувати x0 =
0,5*(1 +
a).
,
в якості початкового значення
використовувати x0 =
0,5*(1 +
a).
8. Знайти максимальний елемент в масиві ai (i=1, (, n), використовуючи очевидне співвідношення max(a1, (, an) = max[max(a1, (, an - 1), an].
9. Вичислити значення y(n)
=
![]() .
.
10. Знайти максимальний елемент в масиві ai (i=1, (, n), використовуючи співвідношення (ділення навпіл) max(a1,(, an) = max[max(a1,(, an/2), max(an/2+1, (, an)].
11. Вичислити значення y(n)
=
 .
.
12. Вичислити твір парної
кількості n
(n ( 2)
співмножників наступного виду
y =
![]() .
.
13. Вичислити y = xn за наступним правилом: y = (xn/2)2 якщо n парне і y = x * yn - 1, якщо n непарне.
14. Вичислити значення
![]() (значення 0! = 1).
(значення 0! = 1).
15. Вичислити y(n)
=
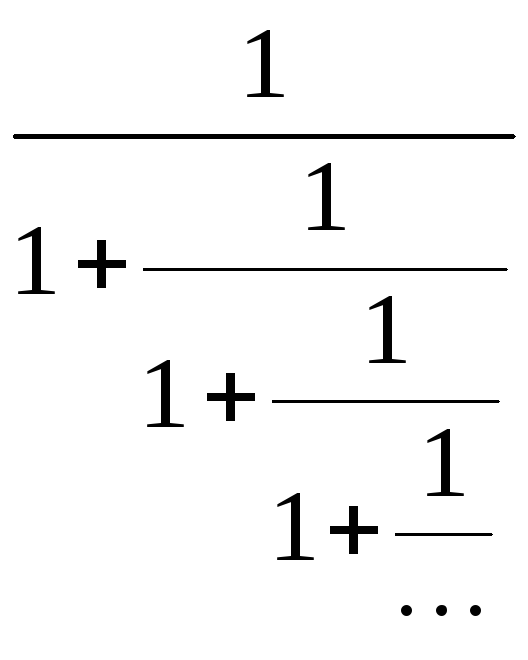 ,
n задає число східців.
,
n задає число східців.
16. У заданому масиві замінити усі числа, що граничать з цифрою «1», нулями.
Контрольні питання
-
Дайте визначення підпрограми.
-
Дайте визначення рекурсії та рекурсивної функції.
-
Що таке прототип функції та в чому полягає його призначення?
-
Поясніть своїми словами механізми роботи рекурсивних функцій.
-
В чому полягає особливість рекурсивної функції?
-
Чи можна вирішити запропоновані задачі без використання рекурсії? Поясніть свою відповідь.

