Файл: Анализ сигналов и их прохождения через линейные радиотехнические цепи.docx
Добавлен: 18.10.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное бюджетное образовательное учреждение
высшего образования Московской области
«Университет «Дубна»
(государственный университет «Дубна»)
Инженерно-физический институт
Кафедра проектирования электроники для установок «мегасайенс»
Курсовая работа
по дисциплине «Теоретические основы радиотехники»
Тема: «Анализ сигналов и их прохождения через линейные радиотехнические цепи»
Выполнил: студент группы 2142
Кононов Артем Александрович
Проверил: проф. Трофимов А.Т.
Оценка _______________________
Дата сдачи «__»___________2022 г.
Дубна
2022 г.
Оглавление
Оглавление
Компьютерная модель сигнала с заданными параметрами 3
Получение аналитического выражение (модели) периодического сигнала 5
Анализ характеристик видеосигнала 7
Анализ характеристик радиосигнала 9
Компьютерная модель сигнала с заданными
параметрами
Для того, чтобы сделать сигналы объектами теоретического изучения и расчётов, следует указать способ их математического описания, то есть создать математическую модель исследуемого сигнала.
Исследуемая форма сигнала представляет собой функцию Эрмита. Она имеет вид:
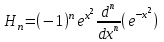 .
.Функция Эрмита пятого порядка описывается следующей формулой:
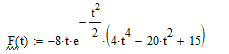
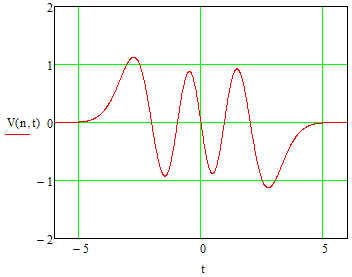
Рис. 1. Компьютерная модель видеосигнала.
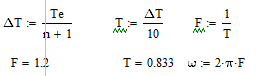
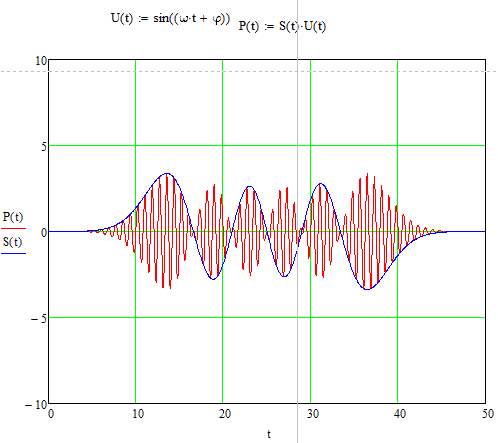
Рис. 2. Компьютерная модель радиосигнала.
Получение аналитического выражение (модели) периодического сигнала
Периодический видеосигнал выразим через одиночную функцию Эрмита третьей степени
, длительностью 50 миллисекунд:.

Рис.3. График периодического видеосигнала
Дискретный по времени график функции выглядит следующим образом:
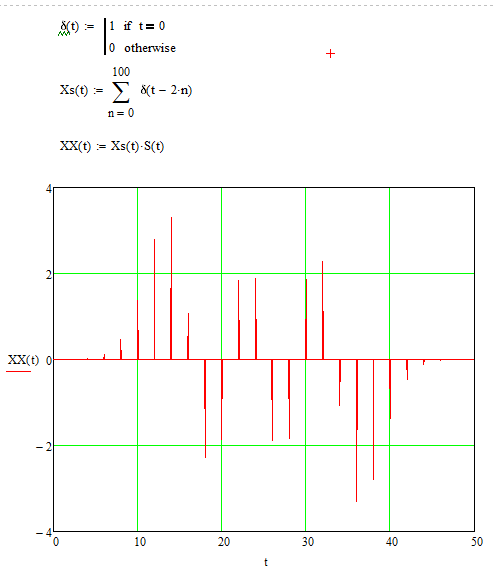
Рис.4. Дискретный по времени график
Квантованный по уровню:
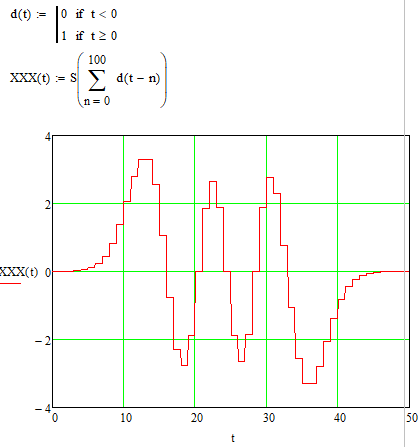
Рис.5. Квантованный по уровню график
Где d(t) ступенчатая функция.
Анализ характеристик видеосигнала
Построим спектры видеосигнала. В виде базовой функции выберем гармонику. Частоту первой гармоники зададим как
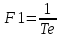 ,
, 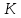 — число суммируемых гармоник.
— число суммируемых гармоник.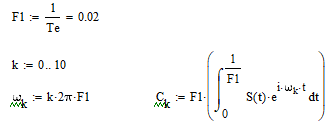
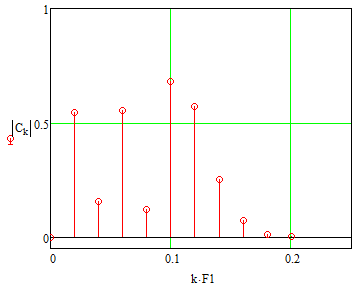
Рис. 6. Амплитудо-частотный спектр заданного видеосигнала.
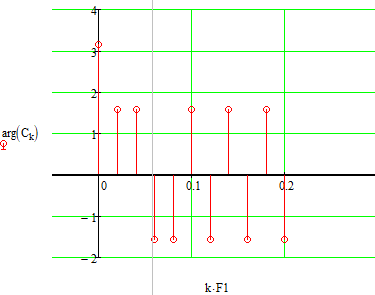
Рис. 7. Фазо-частотный спектр заданного видеосигнала.

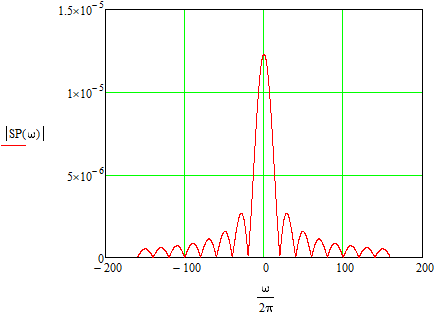
Рис. 8. Спектральная плотность заданного видеосигнала.
Анализ характеристик радиосигнала
Как и в случае с видеоимпульсом, построим амплитудный и фазовый спектры, спектральную плотность и АКФ заданного радиосигнала.
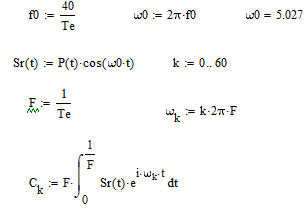
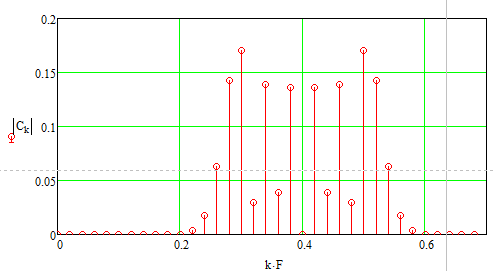
Рис. 9. Амплитудно-частотный спектр заданного радиосигнала.
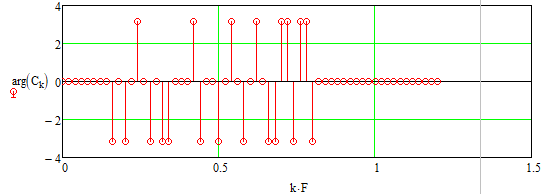
Рис. 10. Фазо-частотный спектр заданного радиосигнала.

