Файл: Луганской народной республики государственное образовательное учреждение высшего образования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«ЛУГАНСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
(ГОУ ВО ЛНР «ЛГПУ»)
Институт профессионального развития
Кафедра физики и методики преподавания физики
ОТЧЕТ
О ПРОХОЖДЕНИИ ПРАКТИКИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ФИЗИЧЕСКИХ ПРОЦЕССОВ (ПРОИЗВОДСТВЕННАЯ)
Студента Филиной Инны Александровны
Курс: 2 Направление подготовки: 44.03.05 Педагогическое образование (с двумя профилями)
Профиль: Физика. Математика
Место прохождения практики: ГОУ ВО ЛНР «ЛГПУ», кафедра физики и методики преподавания физики.
Срок прохождения практики: с 27.02.2023 г. по 11.03.2023 г.
Результаты защиты ___________________ _____________
(количество баллов) (оценка)
Руководитель практики ___________ Н.В. Корчикова
Луганск
2023
ВВЕДЕНИЕ.
Табличные редакторы (иногда их называют также электронные таблицы) на сегодняшний день, одни из самых распространенных программных продуктов, используемые во всем мире. Они без специальных навыков позволяют создавать достаточно сложные приложения, которые удовлетворяют до 90% запросов средних пользователей.
Табличные редакторы появились практически одновременно с появлением персональных компьютеров, когда появилось много простых пользователей не знакомых с основами программирования. Первым табличным редактором, получившим широкое распространение, стал Lotus 1-2-3, ставший стандартом де-факто для табличных редакторов:
· Структура таблицы (пересечения строк и столбцов создают ячейки, куда заносятся данные);
· Стандартный набор математических и бухгалтерских функций;
· Возможности сортировки данных;
· Наличие средств визуального отображения данных (диаграмм).
Microsoft Excel является широко распространенной компьютерной программой, с помощью которой производятся расчеты, составляются таблицы и диаграммы, вычисляются простые и сложные функции. Microsoft Excel – это большая таблица, предназначенная для внесения в нее данных. Важная особенность использования электронной таблицы заключается в автоматическом пересчете результатов, если изменяются значения ячеек. Excel может применяться при выполнении финансовых расчетов, учете и контроле кадрового состава той или иной организации, в построении и обновлении графиков, которые основаны на введенных числах.
Файл, с которым предполагает работу Excel, называется книгой. Она включает в себя несколько рабочих листов, в которых могут содержаться самые разные данные, начиная от таблиц и текстов и заканчивая диаграммами и рисунками.
Раздел 1. Теоретическая часть.
1.1.Основные функции программы Microsoft Excel.
Функция СУММ
Это одна из математических функций. Она нужна, чтобы автоматически посчитать сумму чисел в выбранном диапазоне.
Как работать с функцией
Чтобы получить общую сумму чисел одного столбца, нужно:
-
Выделить диапазон: столбец или ячейки с числами, которые нужно сложить. -
Выбрать Вставка → Функции → СУММ или ∑ → СУММ.
Если поменять действия местами, результат будет одинаковым.
Можно использовать второй вариант:
-
Выбрать первую пустую ячейку в конце диапазона. -
Выбрать ∑ → СУММ. -
Вписать в свободную ячейку значения нужных диапазонов.
Чтобы не использовать инструмент ∑, можно вручную ввести =СУММ в пустой ячейке в конце нужного диапазона.
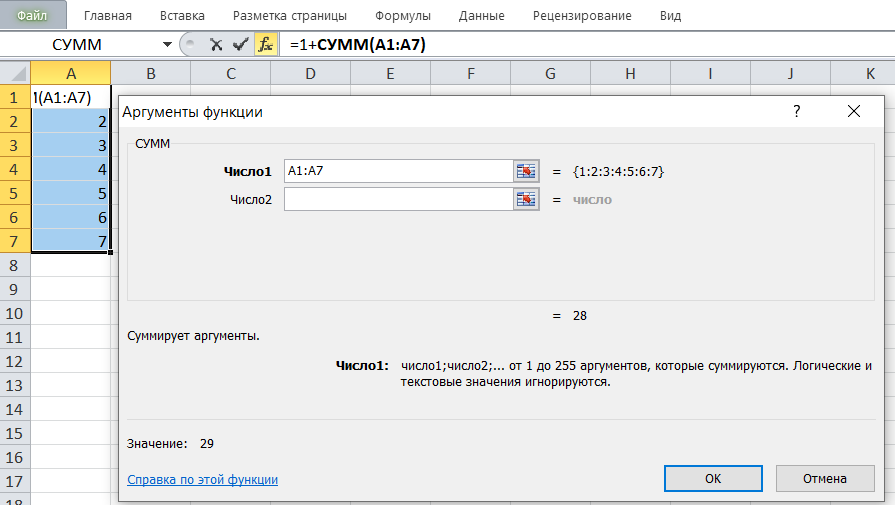
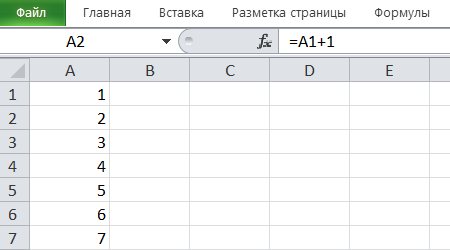
На примере показана формула вычисления и получившееся в результате число. Видно, что общая сумма чисел в диапазоне A1:А7 — 28.
Функция СРЗНАЧ
Эта функция рассчитывает среднее арифметическое в выделенном диапазоне чисел.
Как работать с функцией
Вот как можно вычислить среднее значение:
-
Выбрать первую свободную ячейку в конце диапазона. -
Выбрать ∑ → СРЗНАЧ. -
Вписать в свободную ячейку значения диапазонов.
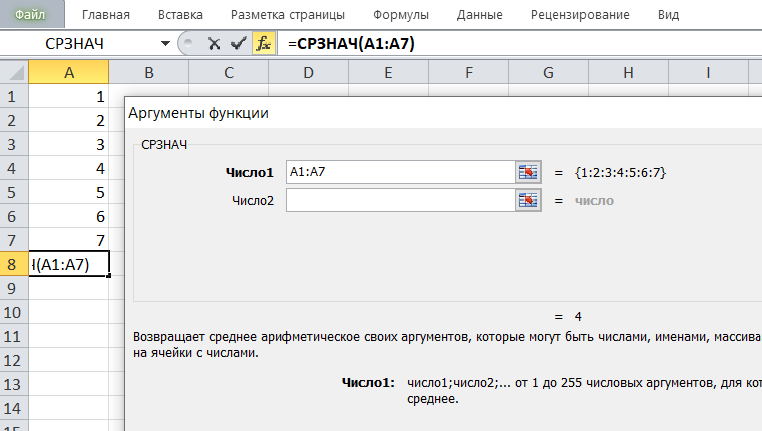
На примере видно, что среднее значение в диапазоне A1:А7 равно 4.
Функция МИН
Одна из статистических функций. Помогает определить минимальное значение из выбранного диапазона чисел. То есть найти самое маленькое число.
Как работать с функцией
Чтобы вычислить минимальное значение, нужно:
-
Выбрать первую свободную ячейку в конце диапазона. -
Выбрать подходящую функцию из списка: ∑ → МИН. -
Вписать в свободную ячейку значения нужных диапазонов.
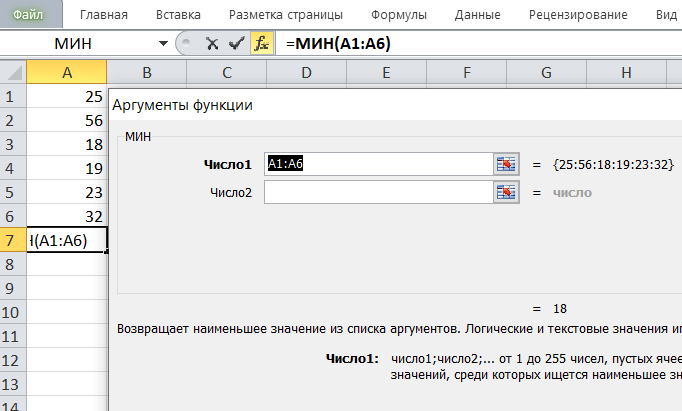
На примере показано минимальное значение в диапазоне A1:А6, которое равно 18, и формула его вычисления.
Функция МАКС
Одна из функций, с помощью которой можно определить максимальное значение из выбранного диапазона чисел. То есть самое большое число.
Как работать с функцией
Максимальное значение можно вычислить так:
-
Выбрать первую свободную ячейку в конце диапазона. -
Выбрать функцию ∑ → МАКС. -
Вписать в свободную ячейку значения нужных диапазонов.
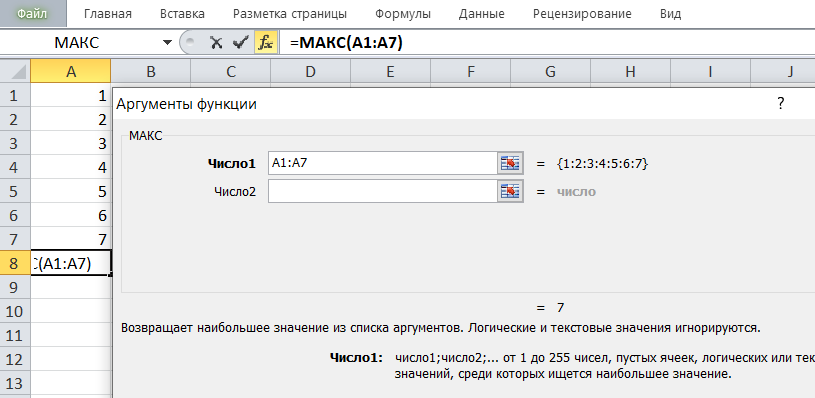
Получилось, что максимальное значение в диапазоне A1:A7 равно 7.
Функция СЧЕТ
Эта функция нужна, чтобы определить количество числовых ячеек в выбранном диапазоне.
Как работать с функцией
Чтобы вычислить количество ячеек, содержащих числа, нужно сделать следующее.
-
Выбрать первую свободную ячейку в конце диапазона. -
Выбрать функцию ∑ → СЧЕТ. -
Вписать в свободную ячейку значения нужных диапазонов.
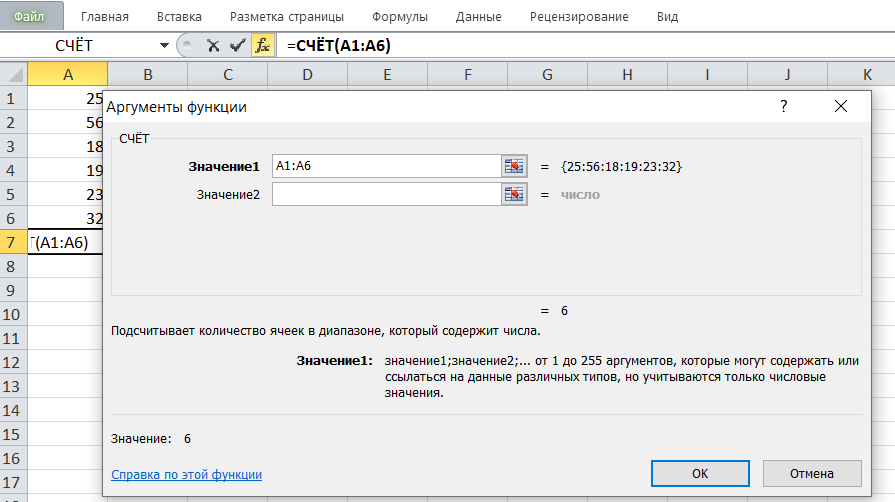
Количество числовых ячеек в диапазоне A1:A6 равно 6.
1.2.Основные этапы работы с электронными таблицами MsExcel
-
ввод данных в ячейки (текст, числа, формулы) -
исправление ошибок -
оформление заголовков -
форматирование таблиц -
копирование -
обработка данных -
построение диаграмм -
печать
Документ, который создается и обрабатывается в MSExcel, называется Книга, он имеет расширение xls или xlsx и состоит из листов, подобно тому, как текстовый документ состоит из страниц, а презентация состоит из слайдов. Листы можно добавлять, удалять, менять местами и переименовывать. Лист представляет собой огромную таблицу.
Каждый лист состоит из строк (которые нумеруются) и столбцов (которые озаглавлены буквами латинского алфавита).
Каждая ячейка такой электронной таблицы имеет имя (адрес), состоящее из названия столбца и номера строки, на пересечении которых она находится. Имя отображается в Поле имен. Выделенная в данный момент ячейка называется активной. В нее можно вводить информацию: текст, числа, формулы.
Ш
Можно пользоваться различными панелями инструментов в зависимости от ваших задач.
Ввод информации в ячейки
Вводить текстовые данные, редактировать и форматировать их можно непосредственно в активной ячейке или в строке формул.Чтобы вводить данные в ячейку, нужно активизировать ее (щелкнуть на ней). Ячейки выбираются мышкой, ввод заканчивается либо щелчком мышки по другой ячейке, либо нажатием клавишиEnter, либо переход на соседнюю ячейку с помощью стрелочек. Можно выделитьдиапазон ячеек (это прямоугольная область таблицы (две ячейки и более)). Чтобы выделить несмежные диапазоны, нужно удерживать нажатой клавишу
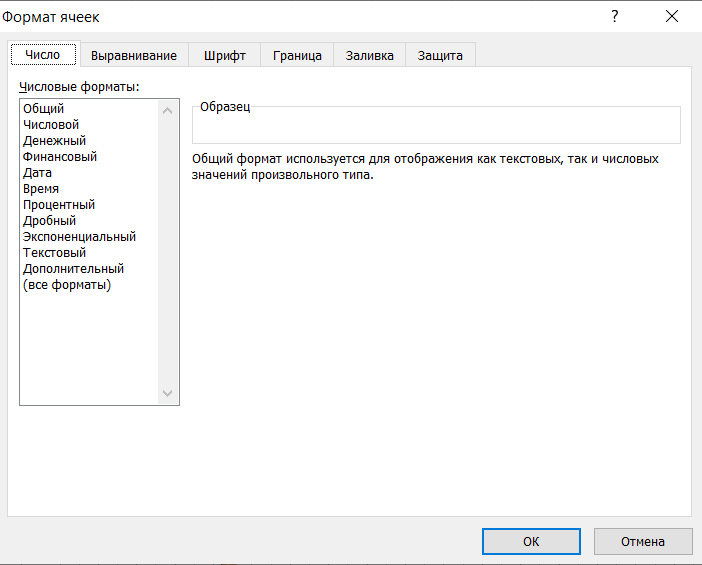
Вводя данные в ячейку, мы можем задать их формат. Для этого необходимо в меню Формат нажать Формат Ячейки и из списка выбрать нужный.
Вводить текстовые данные, которые являются списками, можно с помощью автозаполнения. Например, если строка или столбец должны содержать последовательно дни недели или числа месяца, то достаточно ввести одно число или один день недели. А все последующие дни появятся при копировании. Для этого нужно поместить курсор в правый нижний угол ячейки так, чтобы появился черный крестик, нажать и протянуть.
Построение диаграмм
Для построения диаграмм нужно выделить в таблице необходимые данные (часть таблицы или всю таблицу) и воспользоваться Мастером диаграмм. Результат построения в значительной степени зависит от того, правильно ли выбраны данные для построения. Необходимо выделять таблицу так, чтобы были захвачены названия строк и столбцов и не попадали пустые строки и столбцы.
Выделив таблицу, нажимаем Мастер диаграмм
Диаграмму можно размещать на имеющемся листе, то есть рядом с таблицей, или на отдельном:
Нажимаем Готово, и наша диаграмма построена. Диаграмму можно редактировать через правую кнопку мыши или через меню Правка.
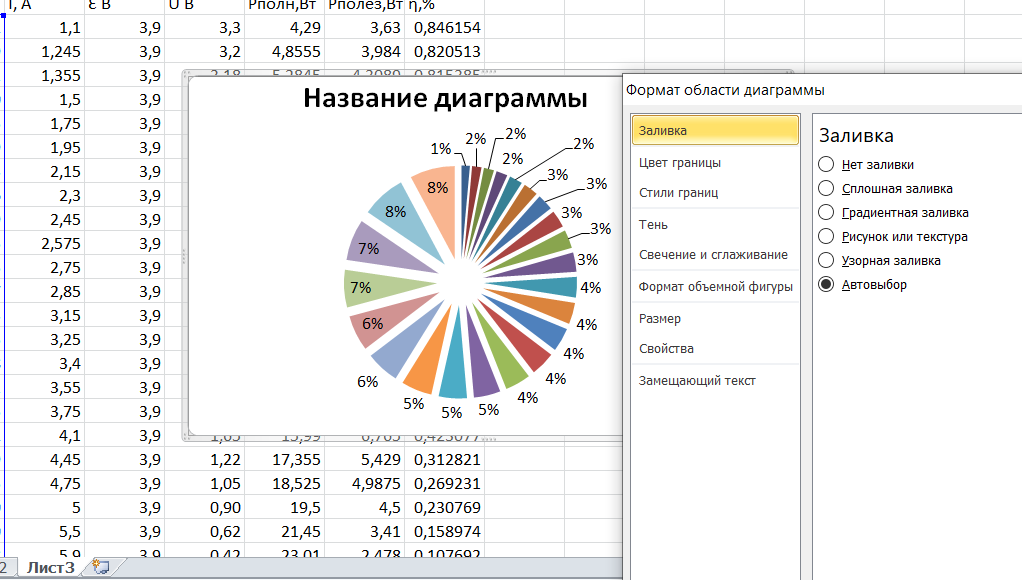
С помощью мастера диаграмм можно также строить графики элементарных и сложных функций, графически решать уравнения и системы уравнений, строить трехмерные поверхности.
Раздел 2. Практическая часть. Выполнение экспериментального задания.
2.1.Описание экспериментальной задачи.
«Исследование зависимости Энергетических
характеристик аккумулятора от нагрузки»
Цель работы: изучить зависимость полезной, полной мощностей и КПД аккумуляторной батареи от силы тока в цепи; экспериментально проверить теоретические выводы.
Краткие теоретические сведения
Аккумуляторы – химические источники тока, в которых электрическая энергия получается за счёт химических реакций. На практике применяют аккумуляторы кислотные и щелочные. В качестве электролита в щелочных аккумуляторах используется 20 % раствор щёлочи в воде. В зависимости от химического состава электродов щелочные аккумуляторы делятся на железо-никелевые, кадмиево-никелевые, цинково-никелевые и т.д. Наиболее часто применяются железо-никелевые и кадмиево-никелевые. Корпуса таких аккумуляторов изготавливают из никелированного железа. Активной массой анодов до зарядки является гидроксил никеля Ni(OH)2.
Схематически реакции зарядки − разрядки можно записать так:
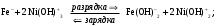
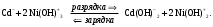
при зарядке аккумулятора активная масса пластин на аноде превращается в гидроксид никеля Ni(OH)2, а активная масса на катоде − в губчатое железо или губчатый кадмий. При разрядке аккумулятора совершается обратный процесс. Рабочее напряжение щелочных аккумуляторов 1,3 … 1,1 В.
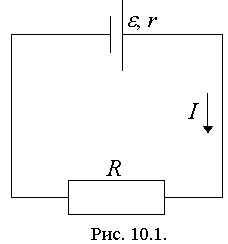
Аккумулятор характеризуется электродвижущей силой и внутренним сопротивлением r.
Мощность, расходуемая источником, частично выделяется во внешней цепи (Pполез), частично на внутреннем сопротивлении (рис. 2.1).
Коэффициент полезного действия источника (КПД) равен:
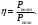 (2.1)
(2.1)Закон Ома для замкнутой цепи может быть записан в форме:
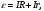 (2.2)
(2.2)где электродвижущая сила источника, I величина тока, R внешнее сопротивление, r внутреннее сопротивление источника.
Величину
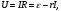 (2.3)
(2.3)называют напряжением во внешней цепи. С нарастанием тока напряжение линейно убывает. При разомкнутой цепи U = .
Домножив уравнение (10.2) на величину тока,
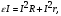 (2.4)
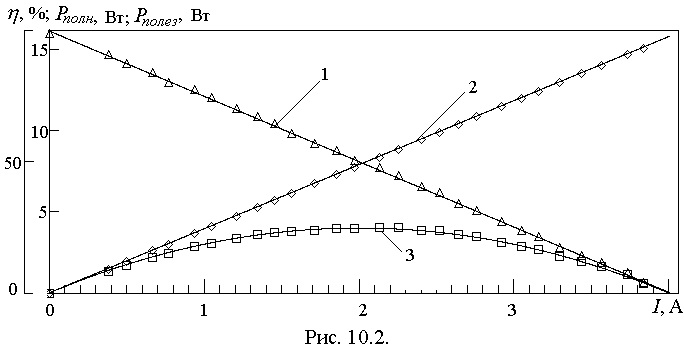
(2.4)получим линейную зависимость полной мощности от величины тока (рис. 10.2)
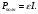 (2.5)
(2.5)Полезная мощность определится выражением:
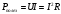 (2.6)
(2.6)Через характеристики источника полезная мощность дает параболическую зависимость от величины тока (рис. 10.2, 3):
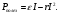 (2.7)
(2.7)Исследование зависимости на максимум показывает, что полезная мощность максимальна при равенстве внешнего и внутреннего сопротивлений.
Зависимость КПД от величины тока линейная (рис. 10.2, 1):
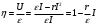 (2.8)
(2.8)Экспериментально, воспользовавшись вольтметром и амперметром, мы можем получить зависимость напряжения во внешней цепи от величины тока U(I) и рассчитать соответствующие зависимости от величины тока полной, полезной мощности и КПД.
Экспериментально требуется исследовать зависимость полезной и полной мощностей и КПД от силы тока. Обработку полученных результатов можно провести с помощью компьютерной программы в XL.
10.2. Порядок выполнения работы
1
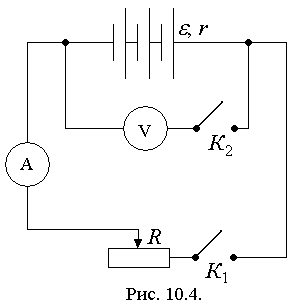
. Собрать электрическую цепь по схеме (рис.10.4).
2. Оставив ключ К1 разомкнутым, замкнуть ключ К2. Записать показания вольтметра. Эту величину можно приблизительно считать равной ЭДС.
3. Введя всё сопротивление R, замкнуть ключ К1. Записать показания амперметра и вольтметра. Увеличивая последовательно силу тока, довести её до максимального значения, записывая при этом в таблицу значения силы тока и напряжения.
Таким образом, прямые измерения – ток (I) и напряжение (U).
4. Вычислить для всех значений силы тока и напряжения
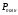 ,
, 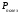 и
и 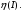
5. Построить на одних и тех же осях графики
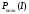 ,
, 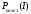 ,
, 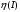 и
и 2.2. Выполнение экспериментальной задачи.
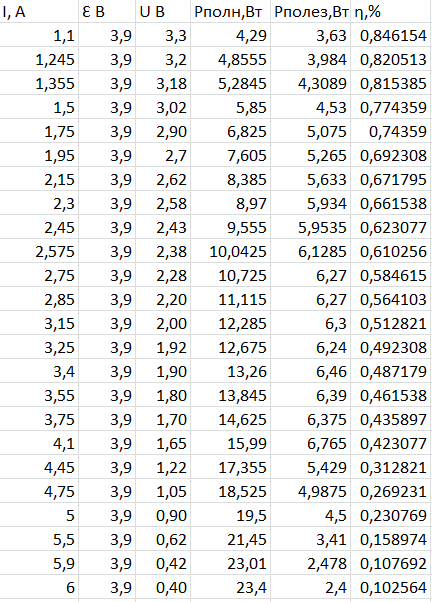
Составим в Microsoft Excel сводную таблицу.
Таблица 2.2.1.Экспериментальные данные и расчетные результаты для исследования зависимости энергетических характеристик аккумулятора от нагрузки.
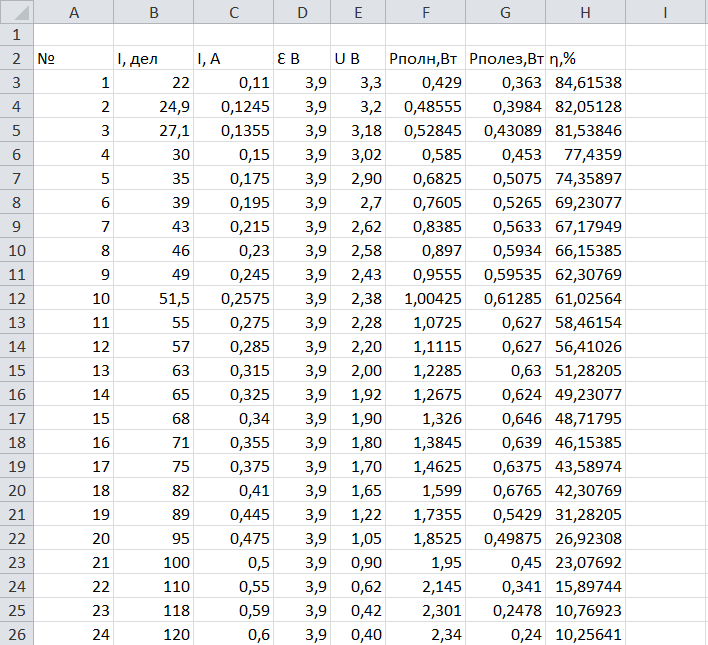
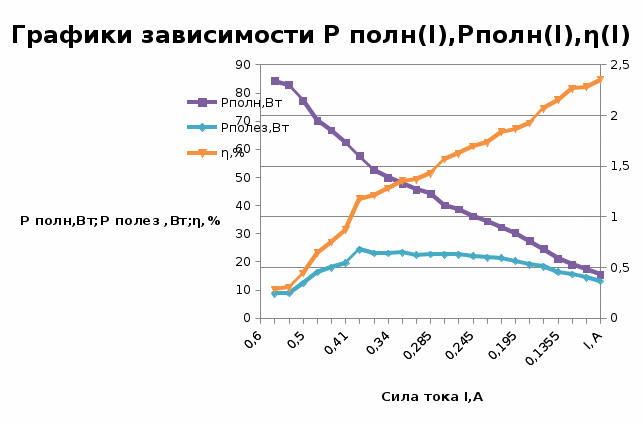
Проведем построение графиков Рполная (Вт) =f(I), Pполезная (Вт) =f(I), η = f(I) в одних осях в XL.
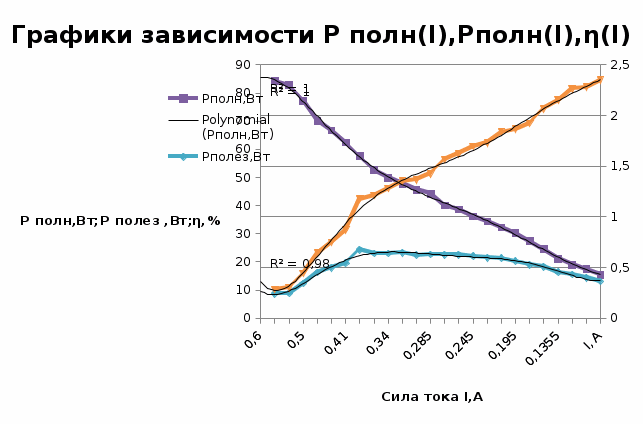
Проведем аппроксимацию полученных графиков.
Заключение.
Компьютерное моделирование и вычислительный эксперимент позволяют свести исследование «нематематического» объекта к решению математической задачи. Этим самым открывается возможность использования для его изучения хорошо разработанного математического аппарата в сочетании с мощной вычислительной техникой. На этом основано применение математики и компьютера для познания законов реального мира и их использования на практике. Компьютерное моделирование имеет ряд преимуществ по сравнению с экспериментальными методами исследования явлений объектов познания. Современные программные продукты позволяют очень быстро решить сложные системы уравнений, с помощью которых описывают физические явления и на основании расчетов постороить зависимости изучаемой величины от ряда факторов. Поэтому компьютерные модели часто используют при исследовании таких явлений, экспериментальное изучение которых представляется сложным и даже непредсказуемым. Формализованность компьютерных моделей позволяет выявить факторы, определяющие свойства изучаемых объектов, мимо которых в экспериментальном изучении ученые проходят.
Изучение физики с применением компьютера, на компьютерных моделях позволяет лучше изучить и, главное, быстрее понять основные физические принципы
В данной работе были освоены принципы работы в программе Microsoft Excel, закреплены навыки работы в ней и знания физических законов.

