Файл: Методы расчета сложных цепей.pdf

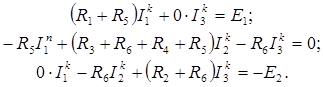
Решая систему уравнений (7), определяем контурные токи .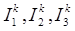

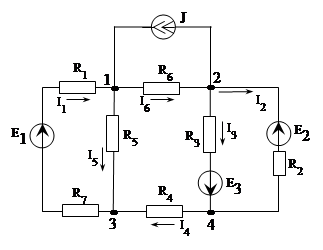
Для однозначного определения токов ветвей выбираем их положительные направления и указываем на схеме (рис. 3).

Токи ветвей

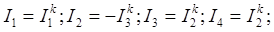
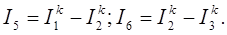
1.3 Метод узловых напряжений (потенциалов)

Сущность метода заключается в том, что в качестве неизвестных принимаются узловые напряжения (потенциалы) независимых узлов цепи относительно одного узла, выбранного в качестве опорного или базисного. Потенциал базисного узла принимается равным нулю, и расчет сводится к определению (q-1) узловых напряжений, существующих между остальными узлами и базисным.

Уравнения узловых напряжений в канонической форме при числе независимых узлов n=q-1 имеют вид

Коэффициент 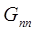 называется собственной проводимостью n-го узла. Собственная проводимость равна сумме проводимостей всех ветвей, присоединенных к узлу n .

Коэффициент 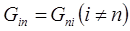 называется взаимной или межузловой проводимостью. Она равна взятой со знаком «минус» сумме проводимостей всех ветвей, соединяющих напрямую узлы i и n .

Правая часть уравнений (9) называется узловым током, Узловой ток равен алгебраической сумме всех источников тока, подключенных к рассматриваемому узлу, плюс алгебраическая сумма произведений ЭДС источников на проводимость ветви с ЭДС

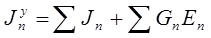
При этом со знаком «плюс» слагаемые записываются в том случае, если ток источника тока и ЭДС источника напряжения направлены к узлу, для которого составляется уравнение.

Приведенная закономерность определения коэффициентов существенно упрощает составление уравнений, которое сводится к записи симметричной матрицы узловых параметров

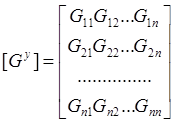
и вектора узловых токов источников

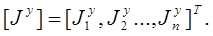
Уравнения узловых напряжений можно записать в матричной форме

.

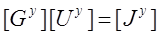Если в какой-либо ветви заданной схемы содержатся только идеальный источник ЭДС (сопротивление этой ветви равно нулю, т.е. проводимость ветви равна бесконечности), целесообразно в качестве базисного выбрать один из двух узлов, между которыми включена эта ветвь. Тогда потенциал второго узла становится также известным и равным по величине ЭДС (с учетом знака). В этом случае для узла с известным узловым напряжением (потенциалом) уравнение составлять не следует и общее число уравнений системы уменьшается на единицу.

---

Решая систему уравнений (9), определяем узловые напряжения, а затем по закону Ома определяем токи в ветвях. Так для ветви, включенной между узлами m и n ток равен

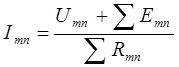
При этом с положительным знаком записываются те величины (напряжения, ЭДС), направление которых совпадает с выбранным координатным направлением. В нашем случае (11) – от узла m к узлу n . Напряжение между узлами 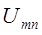 определяется через узловые напряжения

.

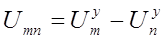Рассмотрим метод узловых напряжений на примере электрической цепи, схема которой представлена на рис. 4.

Рисунок 4

Определяем число узлов (в данном примере число узлов q=4) и обозначаем их на схеме.

Так как схема не содержит идеальных источников напряжения, то в качестве базисного может быть выбран любой узел, например узел 4.

При этом .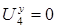

Для остальных независимых узлов схемы (q-1=3) составляем уравнения узловых напряжений в канонической форме.

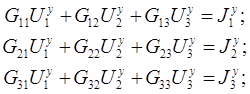
Определяем коэффициенты уравнений.

Собственные проводимости узлов

Взаимные (межузловые) проводимости

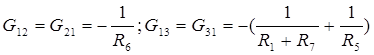
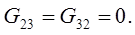
Определяем узловые токи.

Для 1-го узла

.

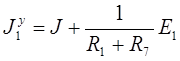Для 2-го узла

.

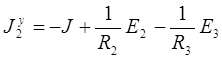Для 3-го узла

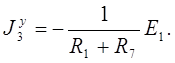
Подставив значения коэффициентов (проводимостей) и узловых токов в уравнения (12), определяем узловые напряжения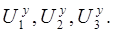 

Прежде чем перейти к определению токов ветвей, задаемся их положительным направлением и наносим на схему (рис. 5).

Токи определяем по закону Ома. Так, например, ток 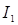 направлен от узла 3 к узлу 1. Так же направлена и ЭДС  этой ветви. Следовательно

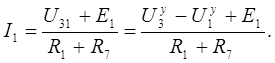
Токи остальных ветвей определяем по тому же принципу

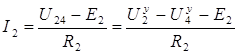
Так как 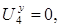то

---

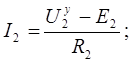
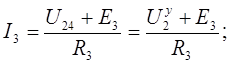
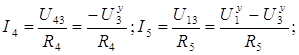
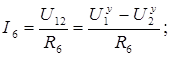
Глава 2. ПРАКТИЧЕСКАЯ ЧАСТЬ.

2.1 Расчет методом контурных токов

Проведем эквивалентное преобразование источника тока в источники ЭДС

Введем контурные токи I₁₁ , I₂₂ , I_33, I₄₄.

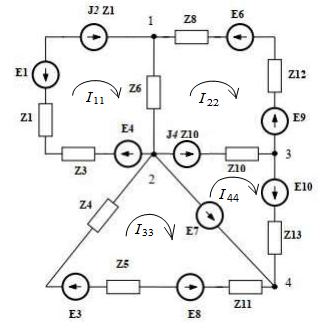
Рисунок 5

I₁₁z₁₁ + I₂₂z ₁₂ + I₃₃z₁₃ + I₄₄z₁₄ = E₁₁

I₁₁z₂₁ + I₂₂z₂₂ + I₃₃z₂₃ + I₄₄z₂₄ = E₂₂

I₁₁z₃₁ + I₂₂z₃₂ + I₃₃z₃₃ + I₄₄z₃₄ = E₃₃

I₁₁z₄₁ + I₂₂z₄₂ + I₃₃z₄₃ + I₄₄z₄₄ = E₄₄

Определим собственные сопротивления контуров:

z₁₁ = z₁ + z₃ + z₆ = j50 + 38 + j20 = 38 + j70 Ом

z₂₂ = z₆ + z₈ + z₁₀ + z₁₂ = j20 + 215 – j75 + 10 = 225 – j55 Ом

z₃₃ = z₄ + z₅ + z₁₁ = 14 + j16 – j75 = 15 – j59 Ом

z₄₄ = z₁₀ + z₁₃ = – j75 + j25 = – j50 Ом

и общие сопротивления контуров:

z₁₂ = z₂₁= – z₆ = – j20 Ом

z₂₄ = z₄₂= – z₁₀ = j75 Ом

Определим собственные ЭДС контуров:

Е₁₁ = J₂z ₁ + Е₄ – Е₁ = j50‧3 +25 – 6 = j150 + 19 В

Е₂₂ = – Е₆ – Е₉ – J₄z ₁₀ = – 4 – 6 + j75‧7 = j525 – 10 В

Е₃₃ = Е₇ – Е₈ + Е₃ = 15 – 9 – 39 = – 33 В

Е₄₄ = J₄z ₁₀ + Е₁₀ – Е₇ = j75‧7 + 13 – 15 = j525 – 2 В

Для определения контурных токов составим систему уравнений:

(39 + j70) I₁₁ – j20 I₂₂ = 19 + j150

– j20 I₁₁ + (225 – j55) I₂₂ – j75 I₄₄ = – 10 + j525

(15 – j59) I₃₃ = – 33

J75 I₂₂ – j50 I₄₄ = – 2 + j525

В результате получим следующие значения контурных токов:

I₁₁ = 1,3713 + j1,9139 А;

I₂₂ = 0,9361 + j5,0435 А;

I₃₃ = – 0,1335 – j0,5253 А;

I₄₄ = – 9,0957 + j7,5252 А;

Находим реальные токи в ветвях:

I₁ = 1,3713 + j1,9139 А;

I₂ = 0,9361 + j5,0435 А;

I₃ = – 0,1335 – j0,5253 А;

I₄ = – 9,0957 + j7,5252 А;

I₅ = + 3,1375 – j1,5553 А;

I₆ = – 3,0152 + j3,5054 А;

2.2 Потенциальная диаграммa

R,Ом ,Ом

Размещено на Allbest.ru

5

1

2

3

---

U, В

4

6

4

Список литературы

1. Атабеков Г.И. Основы теории цепей: Учебник. – СПб.: Издательство «Лань», 2009. - 432 с.

2. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебное пособие для вузов. Под ред. В.П. Бакалова. – М.: Горячая линия – Телеком, 2013. - 596 с.

3. Новиков Ю.Н. Основные понятия и законы теории цепей, методы анализа процессов в цепях: Учебное пособие. – СПб.: Издательство «Лань», 2011. - 368 с.

4. Атабеков Г.И. Теоретические основы электротехники. Линейные электрические цепи: Учебное пособие. – СПб.: Издательство «Лань», 2009. - 592 с.

5. Атабеков Г.И., Купалян С.Д., Тимофеев А.Б., Хухриков С.С. Теоретические основы электротехники. Нелинейные электрические цепи. Электромагнитное поле: Учебное пособие / Под ред. Г.И. Атабекова. – СПб.: Издательство «Лань», 2010. - 432 с.

---