Файл: Методы сортировки данных: эволюция и сравнительный анализ. Примеры использования ( Классы методов сортировки ).pdf

Еще один весьма привлекательных метод обменной сортировки был предложен в 1964 году К.Э. Бэтчером. Его метод далеко не очевиден. В сравнение с методом пузырька он направлен на то, чтобы избежать, казалось бы, неизбежного, а именно того, чтобы число сравнений в алгоритме было равно числу инверсий в исходном файле. Для этого Бетчером был предложен алгоритм поиска возможных сравнений. По сути, этот алгоритм производит сортировку отдельных подпоследовательностей и дальнейшее их слияние. Поэтому такой метод получил название обменной сортировкой со слиянием. С одной стороны, эффективность этого алгоритма не велика, но все недостатки компенсируются одним аспектом – этот алгоритм позволяет извлекать большую выгоду на машинах, позволяющих проводить параллельные вычисления. То есть можно параллельно отсортировать несколько подфайлов, а затем выполнить слияние. Поэтому этот метод также известен как алгоритм параллельной сортировки Бутчера.

1.5 Сортировка посредством выбора

Наконец рассмотрим еще один важный класс методов внутренней сортировки. Идея методов этого класса основана на многократном выборе одного элемента. Простейший алгоритм метода сортировки посредством выбора очевидно представить таким образом:

1. Выбрать наименьший элемент, переслать его в область вывода и заменить значение его ключа на ∞ (значение большее всех имеющихся ключей)

2. Повторять шаг 1 до тех пор, пока все элементы не будут выбраны.

Очевидно, для реализации такого алгоритма требуется присутствие всех сортируемых элементов в области видимости, предварительный поиск максимального ключа, а также дополнительную область памяти для вывода. Но есть очевидный способ упростить описанный алгоритм без использования ∞ и выделения дополнительной области в памяти для последовательного вывода выбранных элементов: для этого выбранный элемент можно переставить в начальную позицию, а элемент из начальной позиции на позицию выбранного[9, с.19]. Таким образом, с каждым шагом необходимо уменьшать рассматриваемую последовательность, отделяя от нее первый элемент. Рассмотрим теперь алгоритм сортировки посредством простого выбора, описанный выше:

D_1. [цикл по j] Выполнить шаги D_2, D_3 при j = 1 .. N

D_2. Найти наименьший из ключей, пусть это будет

D_3. Взаимозаменить и

Скорость работы этого алгоритма можно представить формулой.

(1)

Как видно, она лишь немного меньше скорости выполнения алгоритма простых вставок. Этот алгоритм отличает его простота и очевидность, а также то, что способы его усовершенствовать весьма ограничены. Конечно, существует весьма простой способ улучшения алгоритма простого выбора: разбить сортируемый массив на несколько частей. Мы еще поговорим об этом в главе 2.

1.6 Шаблоны функций с++

Механизм шаблонов в С++ позволяет избежать те препятствия, которые создает сильная типизация этого языка при создании функций и классов, которые применимы к различным типам параметров. В нашем случае необходимо рассмотреть использование шаблонов функций, которое понадобиться нам для реализации выбранного нами алгоритма сортировки.

Создание шаблона функции – это создание алгоритма, который автоматически генерирует различные экземпляры функций для различных типов параметров. Для этого программист должен параметризировать те типы параметров и возвращаемых значений, которые должны изменяться. При этом тело функции остается неизменным. Очевидно, что на роль шаблона лучше всего подходит функция, реализация которой остается инвариантной на некотором множестве экземпляров, различающихся типами данных[6, с.87]. Таквыглядитобъявлениешаблона.

template <class Type>

Type [function name] (Type [parametr1].. [parametrN]) {body}

В данном случае введен тип-параметр Type. Компилятор, в зависимости от того, параметры какого типа будут подставлены в функцию, интерпретирует ее так или иначе. Шаблон может быть конкретизирован или, как иногда говорят инстанцирован, для любого встроенного или определенного пользователем типа. Имя типа-параметра, использованное программистом в объявлении шаблона, может быть использовано как имя обычного типа, например, для объявления переменных.

Для реализации алгоритма сортировки будем использовать шаблон функции, принимающий в качестве параметров адрес первого элемента сортируемого массива, а также размер этого массива в качестве параметра-константы.

template<class TypeName, int size >

void sort( TypeName (&array)[size] ){ // телофункции }

Недостатком такого подхода будет то, что для двух массивов из элементов одного и того же типа, но разных размеров, при подстановке этих массивов в нашу функцию компилятором будут сгенерированы различные экземпляры этой функции. Но тем не менее механизм шаблонов в С++ не имеет альтернативы в использовании для обобщения функций с несколькими параметрами.

2 . Анализ выбранного метода

2.1 Теоретическое обоснование метода

Вновь возвращаемся к алгоритму D, рассмотренному в разделе 1.5:

D_1. [цикл по j] Выполнить шаги D_2, D_3 при j = 1 .. N

D_2. Найти наименьший из ключей , пусть это будет

D_3. Взаимозаменить и

Очевидно, время выполнения этого алгоритма зависит от числа элементов N, числа сравнений C, и числа «правосторонних минимумов» M. Число сравнений в данном алгоритме не зависит от значений ключей и равно:

(2.1)

Число М будет переменной величиной:

(2.2)

Исходя из этого среднее время выполнения такого алгоритма:

(2.3)

Иначе можно ссылаться на порядок числа пересылок. В худшем случае оно равно , в то время как средний порядок числа пересылок равен. Это показывает, что метод простого выбора выгоден, несмотря на свою неизысканность, что выделяет его из ряда прочих методов внутренней сортировки.

Далее рассмотрим способы усовершенствования метода простого выбора. Обратимся снова к алгоритму D. Рассмотрим для начала его второй шаг. Можно ли каким-либо образом усовершенствовать способ поиска минимума? В общем – нет. В любом алгоритме поиска минимума, основанном на сравнении пар, необходимо выполнить как минимум n-1 сравнений. Значит ли это, что скорость выполнения алгоритма, основанного на сравнении пар, будет пропорциональна ? В общем – нет. По крайней мере, в нашем алгоритме имеется еще и вторая часть. И даже простое ее усовершенствование приведет к ощутимому результату. Рассмотрим, например, последовательность из 16 чисел, которую необходимо отсортировать (рис. 1).

Рис. 2. Пример сортировки улучшенным методом выбора

Проведем довольно простое усовершенствование: разобьем 16 чисел на четыре группы, по четыре числа в каждой. Теперь поиск минимума будет производиться для каждой группы. После этого поиск минимума происходит среди минимальных элементов каждой из групп. На следующем шаге цикла требуется повторить поиск минимума уже только в одной группе и сравнить его с уже имеющимися элементами из других групп; и так далее до того, пока не останется элементов для сравнения. Конечно, этот способ требует более сложного алгоритма и дополнительной памяти для области вывода. Но, если N – точный квадрат, то массив разбивается на √N групп, по √N элементов в каждой. Таким образом, каждый выбор (кроме первого) требует √N-1 сравнений, плюс √N-1 сравнений среди наименьших элементов групп. Тогда скорость работы алгоритма получается порядка O(N√N), что в сравнении с гораздо предпочтительней.

Такой метод был назван метод квадратичного выбора и впервые был опубликован в 1956 году Э.Х. Френдом. Автор обобщил эту идею и описал возможность создания метода кубического выбора (массив делится на групп, по подгрупп с элементами), выбора четвертой степени и т. д. Итак, Френд пришел к выбору n-ой степени, который отражается в методе выбора из бинарного дерева.

Этот весьма любопытный метод напоминает систему турнира на выбывание. Для определения минимального элемента при представлении сортировки в виде дерева происходит за сравнений. А для определений минимума из оставшихся с каждым шагом требуется не более сравнений. Итого суммарная скорость выполнения алгоритма будет равна приблизительно . Но с другой стороны для реализации такого метода потребуется дополнительный массив с индексами вышедших вверх элементов после каждого круга сравнений, так как та запись, в которой он располагался до этого, будет заменена на бесконечность; к тому же потребуется и дополнительная область вывода. Таким образом, встает вопрос: можно ли обойтись без замены элементов на бесконечности и тем самым избежать довольно больших затрат памяти? Решением этого вопроса является метод, представленный ниже.

Пирамидальная сортировка основана на последовательной перестройке исходного массива в пирамиду таким образом, что на вершине находится наибольший элемент. Сам метод был придуман Дж. У. Дж. Уильямсом в 1964 году. Эффективную его реализацию предложил Р. У. Флойд в том же году. Предложенный им алгоритм преобразует исходный файл в пирамиду, а затем многократно исключает вершину, расставляя элементы в соответствующем порядке. Этот алгоритм очень громоздок и в то же время довольно изыскан. Скорость его работы оценивается в среднем формулой (2.3):

, (2.4)

- что не лучше скорости алгоритмов Шелла и быстрой сортировки. Но в отличие от прочих быстрых алгоритмов, в которых худшее значенье скорости достигает , скорость алгоритма пирамидальной сортировки всегда будет не больше , что делает этот алгоритм очень выгодным для сортировки массивов с большим числом инверсий. На этом перейдем к реализации выбранного нами алгоритма сортировки.

2.2 Реализация алгоритма

Для реализации алгоритма сортировки посредством простого выбора (алгоритм D) мы будем использовать язык программирования C++. Для этого составим блок-схему нашего алгоритма с использованием цикла с заданным числом повторений (рис 2). Данный алгоритм будет сортировать массив array, размера size в порядке неубывания. Для реализации алгоритма потребуется использовать один вложенный цикл, реализующий поиск минимума. Как видно на схеме этот цикл (блок 5) производит поиск минимума только среди элементов, которые еще не были выбраны – это позволяет избежать замены выбранных элементов на бесконечность. Блок 7 реализует перестановку выбранного минимума с первым элементом рассматриваемого подмассива. На следующем шаге главного цикла происходит установка счетчика count на элемент вперед и инициализация переменной min значением из подмассива, огражденного слева элементом массива с индексом, соответствующим значению счетчика.

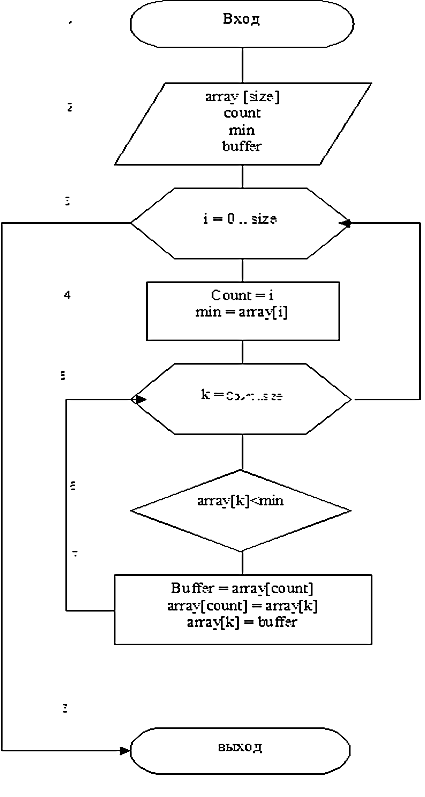
Рис.3. Блок-схема алгоритма сортировки посредством простого выбора

Теперь перейдем непосредственно к кодированию этого алгоритма на языке C++ с помощью компилятора C++Builder 6. Для реализации тестирования нашего алгоритма необходимо использовать шаблон функции С++. Реализация такого шаблона представлена в программе 1.

Программа 1.

#include<stdio.h> // подключение модулей

#include <dos.h> // ……………..

#include <time.h> // ……………..

template<class Type, int size >// объявлениешаблона

int sort( Type (&array)[size] ) // объявлениефункции

{

struct time t; // объявление переменной типа time

int t1, t2, ti; // объявление переменных для расчета времени

работы цикла 1

gettime( &t ); // возвращение системного времени

t1 = t.ti_hund; // запись сотых долей секунды системного времени в

переменную t1

int k = 0, j = 0; // объявление счетчика

Type min = array[0], buf; // объявление переменных для поиска

минимума и перестановки элементов

for( intx = 0; x<size; ++x ){ // цикл 1

k = x; // установка счетчика

min = array[x]; // установка нового значения минимума

for( int i = x+1; i < size; ++i ) // цикл 2 для поиска минимума в

массиве

if( min >= array[i] ){

min = array[i];

j = i; // запоминание позиции минимума в массиве