Добавлен: 29.02.2024
Просмотров: 74
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 1. Основные структуры алгоритмов
1.1 Понятие и основные свойства алгоритмов
1.2 Свойства и способы описания алгоритма
1.3 Основные структуры алгоритмов
Глава 2. Сравнительный анализ структур алгоритмов
2.1 Анализ сложности и эффективности алгоритмов
Глава 3. Примеры известных алгоритмов
3.2 Алгоритм перебора делителей
Сложность алгоритма – это величина, отражающая порядок величины требуемого ресурса (времени или дополнительной памяти) в зависимости от размерности и сложности задачи [8, C.56].
В таком случае, необходимо ввести временную T(n) и пространственную V(n) переменную сложности алгоритма. При анализе и рассмотрении оценок сложности будет использоваться только временную сложность. Пространственная сложность оценивается таким же образом [8, C.57].
Самым простым способом оценки является экспериментальный, т.е. ввести исходные данные в алгоритм и осуществить полученную программу на нескольких задачах, стараясь оценивать все возможные факторы, анализируя время совершения действий программы. Однако этот конкретный метод имеет ряд недостатков и просчетов. Во-первых, экспериментальное программирование – это дорогостоящий процесс, который затрачивает временные и системные ресурсы. Во-вторых, следует учитывать, что на время выполнения действий программы влияют важные факторы:
1) временная сложность алгоритма программы;
2) качество скомпилированного кода исполняемой программы и наличие в нем ошибок;
3) конкретные машинные инструкции, используемые для выполнения действий программы [8, C.35].
Присутствие второго и третьего факторов не разрешают пользоваться типовыми единицами измерения временной сложности алгоритма (секунды, минуты и т.п.), так как в таком случае можно получить самые разные результаты для одного и того же алгоритма, если использовать в данном случае различных программистов (которые напишут алгоритм каждый по-своему), разные компиляторы, языки программирования и разные вычислительные машины.
Чаще всего временная сложность алгоритма находится в прямой зависимости от числа входящих данных. Обычно говорят, что временная сложность алгоритма имеет порядок T(n) от входных данных размера n. Точно определить величину T(n) на практике представляется довольно трудно. Поэтому прибегают к асимптотическим отношениям с использованием O-символики.
Когда используется обозначение символики O(), имеется в виду не точное время исполнения задачи, а только его верхний предел, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n2), имеют в виду, что время исполнения задачи растет не быстрее, чем квадрат количества элементов [11].
На практике время исполнения алгоритма зависит не только от количества входящих данных, но и от их типов и значений, к примеру, время работы некоторых алгоритмов сортировки значительно уменьшается, если первоначальные данные частично упорядочены, тогда как другие методы оказываются не так чувствительны к этому фактору. Чтобы учитывать этот факт, полностью сохраняя при этом возможность анализировать алгоритмы без зависимости от вводных данных, различают: – максимальную сложность, или сложность наиболее неблагоприятного случая, когда алгоритм работает дольше всего; – среднюю сложность – сложность алгоритма в среднем; – минимальную сложность – сложность в наиболее благоприятном случае, когда алгоритм справляется быстрее всего.
2.2 Оптимизация алгоритмов
В настоящее время компьютерные науки не накопили достаточное количество информации для того, чтобы задача минимизации затрат и рабочих ресурсов могла быть представлена с обычной для математики определенностью. Этому мешает сразу несколько факторов.
Во-первых, весьма сложно сформулировать нужный критерий оптимизации, который бы имел одновременно и безусловное практическое значение и однозначно определенный в математическом плане. К примеру, можно поставить задачу минимизации числа выполняемых команд машины Тьюринга – критерий, хорошо определенный математически; но совсем неясно его практическое значение, поскольку маловероятно реально существующая программа на реальном компьютере будет моделировать машину Тьюринга. Возможно поставить задачу минимизации времени выполнения данной программы на реальной машине –понятный с практической точки зрения критерий. Однако нельзя будет решить задачу оптимизации математическими методами, так как затраты времени на выполнение зависит (чаще всего весьма значительно) от архитектуры ЭВМ, а архитектуру современных компьютером невозможно описать маленьким количеством параметров. Так же исключительно важно, что программа, работающая быстрее и эффективнее остальных на одном компьютере, вполне может оказаться не самой быстродействующей на другом. Существуют даже специальные программы с общим названием benchmark, предназначенные для оценки архитектур персональных компьютеров [2].
Во-вторых, не совсем понятно, что такое сложность задачи. Ее можно было бы обозначить как минимальную из возможных сложностей алгоритмов, которые решают эту задачу. Но можно ли вычислить алгоритм минимальной сложности (как найти доказательства тому, что полученный алгоритм действительно минимальный или, напротив, не соответствует требованиям)? Есть ли возможности усовершенствовать алгоритм и насколько сложен поиск этого минимума – эти вопросы связаны с нижней оценкой сложности алгоритмов (а не верхней, как в предыдущих шагах) [8, C.67].
Существует несколько самостоятельных способов оптимизации программ, из которых можно выделить два:
– оптимизация, которая напрямую связана с выбором метода построения алгоритма;
– оптимизация, связанная с выбором методов представления исходных данных в программе [2].
Графически способ оптимизации программ представлен на рис. 2.1.
Способы оптимизации программ
Оптимизация, напрямую связанная с выбором метода построения алгоритма
Оптимизация, связанная с выбором методов представления исходных данных в программе
Рис.2.1 Способы оптимизации программ
Первый способ оптимизации имеет более глобальный характер и ведет к уменьшению порядка функции сложности. Он зависит от того, как поставленная в программе задача разбивается на подзадачи, насколько это разбиение подходит самой задаче или является только искусственным приемом. Общим руководящим подходом здесь является последовательность действий, обратная анализу алгоритмов.
Следующий вид оптимизации, не меняя целиковую структуры программы, приводит к экономии памяти и ресурсов, и/или упрощению работы со структурами вводных данных, повышению эффективности работы вспомогательных процедур, обеспечивающих «интерфейс» между прикладным уровнем (на котором мыслим в терминах высокоуровневых объектов – то графов, матриц, текстов и т. д.) и машинным уровнем, использующих простейшие типы данных (цифры, символы, указатели) [2].
Результатом данного процесса как правило является уменьшение коэффициентов при некоторых слагаемых в функции сложности (при удачной оптимизации – при наиболее значимом слагаемом), но порядок функции сложности остается тем же.
Оба вида оптимизации дополняют друг друга и могут применяться совместно.
Глава 3. Примеры известных алгоритмов
3.1 Алгоритм Евклида
Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις – «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля (IV век до н. э.). В «Началах» Евклида он описан дважды – в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков [15, C.7].
Историками математики было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел [4].
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД [13, C.93].
Описание алгоритма нахождения НОД делением:
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Приведем пример алгоритма Евклида:
Найти НОД для 30 и 18.
30/18 = 1 (остаток 12)
18/12 = 1 (остаток 6)
12/6 = 2 (остаток 0)
Конец: НОД – это делитель. НОД (30, 18) = 6.
Графически алгоритм Евклида представлен на рис. 3.1
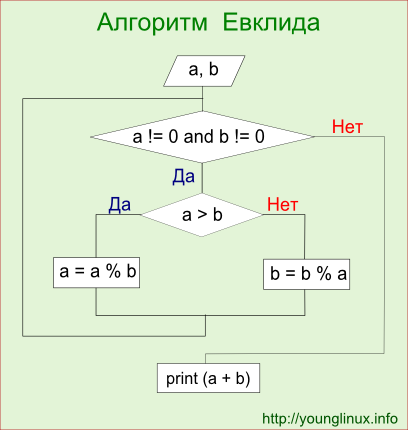
Рис. 3.1 Алгоритм Евклида [14]
Геометрический алгоритм Евклида можно представляет собой: Пусть даны два отрезка длины a и b. Вычтем из большего отрезка меньший и заменим больший отрезок полученной разностью. Повторяем эту операцию, пока отрезки не станут равны. Если это произойдёт, то исходные отрезки соизмеримы, и последний полученный отрезок есть их наибольшая общая мера. Если общей меры нет, то процесс бесконечен. В таком виде алгоритм описан Евклидом и реализуется с помощью циркуля и линейки.
Для иллюстрации алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала от 1071 отнимем кратное значение 462, пока не получим разность меньше, чем 462. Мы должны дважды отнять 462, (q0 = 2), оставаясь с остатком 147:
1071 = 2 × 462 + 147.
Затем от 462 отнимем кратное значение 147, пока не получим разность меньше, чем 147. Мы должны трижды отнять 147 (q1 = 3), оставаясь с остатком 21:
462 = 3 × 147 + 21.
Затем от 147 отнимем кратное значение 21, пока не получим разность меньше, чем 21. Мы должны семь раз отнять 21 (q2 = 7), оставаясь без остатка:
147 = 7 × 21 + 0.
Таким образом последовательность a > b >r1>r2>r3> … >rn в данном конкретном случае будет выглядеть так:
1071 > 462> 147 > 21.
Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462) = 21.
В табличной форме шаги были следующие (таблица 3.1):
Таблица 3.1 Последовательность решения алгоритма Евклида
|
Шаг k |
Равенство |
Частное и остаток |
|
0 |
1071 = q0 462 + r0 |
q0 =2 и r0 = 147 |
|
1 |
462 = q1 147 + r1 |
q1 = 3 и r1 = 21 |
|
2 |
147 = q2 21 + r2 |
q2 = 7 и r2 = 0 алгоритм заканчивается |
Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA, широко распространённого в электронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений, при построении непрерывных дробей, в методе Штурма. Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например, таких как теорема Лагранжа о сумме четырёх квадратов и основная теорема арифметики.
3.2 Алгоритм перебора делителей
Перебор делителей – это алгоритм, предназначенный для определения, какое число перед нами: простое или составное [4].
Алгоритм заключается в последовательном делении заданного натурального числа на все целые числа, начиная с двойки и заканчивая значением меньшим или равным квадратному корню тестируемого числа. Если хотя бы один делитель делит тестируемое число без остатка, то оно является составным. Если у тестируемого числа нет ни одного делителя, делящего его без остатка, то такое число является простым [5, C.119].
Для иллюстрации проведем перебор делителей числа n = 29. i – возможные делители n.
[n1/2] = 5
Решение задачи представим в таблице 3.2.
Таблица 3.2 Решение алгоритмом «перебора делителей» для числа 29
|
i |
n % i |
|
2 |
1 |
|
3 |
2 |
|
4 |
1 |
|
5 |
4 |
Так как ни один из остатков деления 29 не равен 0, то 29 объявляется простым.
Пусть теперь n = 7399, тогда[n1/2] = 86
Решение задачи представим в таблице 3.3.
Таблица 3.3 Решение алгоритмом «перебора делителей» для числа 7399
|
i |
n % i |
|
2 |
1 |
|
3 |
1 |
|
4 |
3 |
|
5 |
4 |
|
6 |
1 |
|
7 |
0 |
