Добавлен: 29.02.2024
Просмотров: 78
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 1. Основные структуры алгоритмов
1.1 Понятие и основные свойства алгоритмов
1.2 Свойства и способы описания алгоритма
1.3 Основные структуры алгоритмов
Глава 2. Сравнительный анализ структур алгоритмов
2.1 Анализ сложности и эффективности алгоритмов
Глава 3. Примеры известных алгоритмов
3.2 Алгоритм перебора делителей
[ n 1 / 2 ] = 86 {\displaystyle [n^{1/2}]=86}
Так как остаток деления 7399 на 7 равен 0, то 7399 не является простым. Графически алгоритм перебора делителей представлен на рис. 3.2.
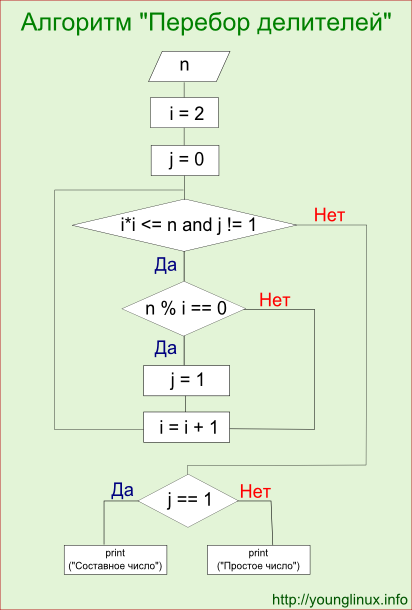
Рис. 3.2 Алгоритм «перебора делителей» [14]
В практических задачах данный алгоритм применяется редко ввиду его большой вычислительной сложности, однако его применение оправдано в случае, если проверяемые числа относительно невелики, так как данный алгоритм довольно легко реализуем.
3.3 Алгоритм решето Эратосфена
Решето Эратосфена – это алгоритм нахождения простых чисел до заданного числа n. В процессе выполнения данного алгоритма постепенно отсеиваются составные числа, кратные простым, начиная с 2.
Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые. Эратосфен дал таблицу простых чисел до 1000 (см. Приложение 3).
Схематично алгоритм «Решето Эратосфена» представлен на рис. 3.3.
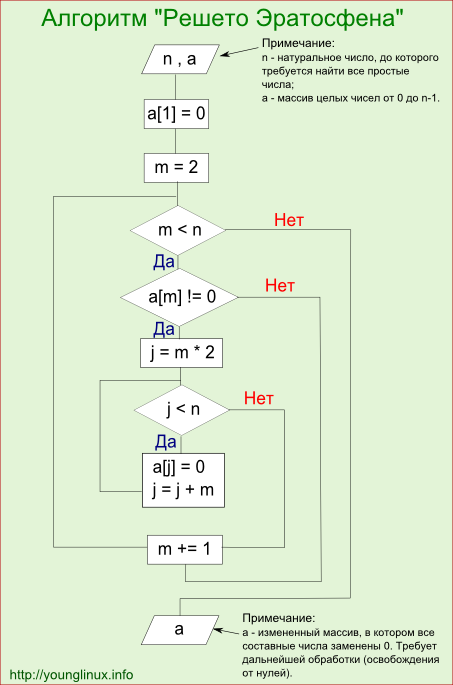
Рис. 3.3 Алгоритм «Решето Эратосфена» [14]
Приведем пример алгоритма «Решето Эратосфена».
Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
- Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
- Пусть переменная p изначально равна двум – первому простому числу.
- Зачеркнуть в списке числа от 2p до n считая шагами по p (это будут числа кратные p: 2p, 3p, 4p, …).
- Найти первое не зачеркнутое число в списке, большее чем p, и присвоить значению переменной p это число.
- Повторять шаги 3 и 4, пока возможно.
Теперь все не зачеркнутые числа в списке – это все простые числа от 2 до n.
На практике, алгоритм можно улучшить следующим образом. На шаге № 3 числа можно зачеркивать начиная сразу с числа p2, потому что все составные числа меньше него уже будут зачеркнуты к этому времени. И, соответственно, останавливать алгоритм можно, когда p2 станет больше, чем n. Также, все простые числа (кроме 2) – нечётные числа, и поэтому для них можно считать шагами по 2p, начиная с p2.
Приведем пример алгоритма «Решето Эратосфена» для n = 30.
Запишем натуральные числа, начиная от 2, до 30 в ряд:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Первое число в списке, 2 – простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 2 (то есть, каждое второе, начиная с 22 = 4):
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Следующее не зачеркнутое число, 3 – простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 3 (то есть, каждое третье, начиная с 32 = 9):
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Следующее не зачёркнутое число, 5 – простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 5 (то есть, каждое пятое, начиная с 52 = 25):
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Следующее не зачеркнутое число –7. Его квадрат, 49– больше 30, поэтому на этом работа завершена. Все составные числа уже зачеркнуты:
2 3 5 7 11 13 17 19 23 29
Подобно всем алгоритмам, решето Эратосфена имеет ограничения. Например, оно неэффективно при поиске очень больших простых чисел. Но в то же время цель этого алгоритма – поиск всех простых меньших, чем определенная верхняя граница. Ясно, что такой поиск невыполним, если граница слишком велика.
Суммируя ограничения, накладываемые назначением алгоритма, отметим два его слабых места: решето требует уйму компьютерной памяти и должно проделать слишком много витков цикла. К его достоинствам можно отнести простоту программирования и, кроме того, нам не нужно вычислять отдельные делители.
Заключение
Целью данной курсовой работы являлось изучение базовых структур алгоритмов, проведения их сравнительного анализа и изучения их применения на практике.
На проведенной проделанной работы можно сделать следующие выводы.
Во всех сферах своей деятельности, и частности в сфере обработки информации, человек сталкивается с различными способами или методиками решения задач. Они определяют порядок выполнения действий для получения желаемого результата – мы можем трактовать это как первоначальное или интуитивное определение алгоритма. Некоторые дополнительные требования приводят к определению алгоритма.
Алгоритм – это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых элементарных операций для решения задачи, общее для класса возможных исходных данных.
Понятие алгоритма – одно из основных в программировании и информатике. Это последовательность команд, предназначенная исполнителю, в результате выполнения которой он должен решить поставленную задачу. Алгоритм должен описываться на формальном языке, исключающем неоднозначность толкования. Исполнитель может быть человеком или машиной. Исполнитель должен уметь выполнять все команды, составляющие алгоритм. Множество возможных команд конечно и изначально строго
Алгоритм обладает следующими основными свойствами: дискретностью; определенностью (детерминированностью, точностью); массовостью; результативностью; формальностью.
При всем разнообразии решаемых задач в них можно выделить три основных (канонических) вида алгоритмических структур: линейную, разветвленную и циклическую. С помощью этих трех видов структур можно построить алгоритм любой сложности.
Запись алгоритма на формальном языке называется программой. Иногда само понятие алгоритма отождествляется с его записью, так что слова «алгоритм» и «программа» — почти синонимы. Небольшое различие заключается в том, что под алгоритмом, как правило, понимают основную идею его построения. Программа же всегда связана с записью алгоритма на конкретном формальном языке.
Благодаря развитию информационных технологий и алгоритмам мы сегодня имеем возможность быстро находить информацию в интернете (в частности, искать по картинкам), находить кратчайшие пути, анализировать геномы и так далее. Алгоритмы используются практически во всех областях жизни.
Список использованной литературы
- Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы: Пер. с англ.: – М.: Издательский дом «Вильямс», 2001 г. –384 с., ил.
- Библиотека программиста // http://www.programmer-lib.ru/assemw_page.php?id=1 (дата обращения 27.07.2018)
- Брой, М. Информатика. Основополагающее введение: В 4-х ч. Ч.1. / М. Брой. – М.: Диалог-МИФИ, 1996. – 299 с.
- Википедия // https://ru.wikipedia.org/wiki (дата обращения 11.08.2018)
- Вирт, Н. Алгоритмы и структуры даны учебник / Н. Вирт. – М.: Мир, 1989. – 360 с.
- Информатика: базовый курс: учебник для студентов вузов, бакалавров, магистров, обучающихся по направлению «Информатика» / О.А. Акулов, Н.В. Медведев. 6-е изд., испр. и доп. – М.: Издательство «Омега-Л», 2009. – 574 с.
- Кадырова, Г.Р. Основы алгоритмизации и программирования: учебное пособие / Г.Р. Кадырова. – Ульяновск, УлГТУ, 2014 – 95 с.
- Каймин, В.А. Информатика: учебник / В.А. Каймин. – М.: Проспект, 2011. – 272 с.
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: МЦНМО, 2001 г. – 960 с., 263 ил.
- Макконнел Дж. Анализ алгоритмов. Вводный курс. – М.: Техносфера, 2002 г. –304 с.
- Самуйлов С.В. Методика сравнительного анализа алгоритмов на примере алгоритмов последовательного поиска // Концепт, 2014. – №9. // https://e-koncept.ru/2014/14236.htm (Дата обращения 15.08.2018)
- Семакин, И.Г. Основы алгоритмизации и программирования: учебник для студ. учреждений сред. проф. Образования / И.Г. Семакин, А.П. Шестаков. – 3-е изд. стер. – М.: Издательский центр «Академия», 2012. – 400 с.
- Соболь, Б.В. Информатика и программирование: учебное пособие / Б.В. Соболь. – Ростов н/Д: Феникс, 2006 – 354 с.
- Теория алгоритмов // https://inf1.info (дата обращения 01.08.2018)
- Тихомиров, В. М. Великие математики прошлого и их великие теоремы. – 2-е изд., испр. – МЦНМО, 2003. – 16 с.
Приложение 1. Основные элементы блок--схемы
Приложение 2. Структура разветвляющегося алгоритма
Начало
Объявление переменных
Ввод данных
Действия
Условие
Действия 1
Действия 2
Окончание
Вывод данных
Окончание
Приложение 3. Таблица алгоритма «Решето Эратосфена»
|
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
|
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
|
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
|
97 |
101 |
103 |
107 |
109 |
113 |
127 |
131 |
|
137 |
139 |
149 |
151 |
157 |
163 |
167 |
173 |
|
179 |
171 |
191 |
193 |
197 |
199 |
211 |
223 |
|
227 |
229 |
233 |
239 |
241 |
251 |
257 |
263 |
|
269 |
271 |
277 |
281 |
283 |
293 |
307 |
311 |
|
313 |
317 |
331 |
337 |
347 |
349 |
353 |
359 |
|
367 |
373 |
379 |
383 |
389 |
397 |
401 |
409 |
|
419 |
421 |
431 |
433 |
439 |
443 |
449 |
457 |
|
461 |
463 |
467 |
479 |
487 |
491 |
499 |
503 |
|
509 |
521 |
523 |
541 |
547 |
557 |
563 |
569 |
|
571 |
577 |
587 |
593 |
599 |
601 |
607 |
613 |
|
617 |
619 |
631 |
641 |
643 |
647 |
653 |
659 |
|
661 |
673 |
677 |
683 |
691 |
701 |
709 |
719 |
|
727 |
733 |
739 |
743 |
751 |
757 |
761 |
769 |
|
773 |
787 |
797 |
809 |
811 |
821 |
823 |
827 |
|
829 |
839 |
853 |
857 |
859 |
863 |
877 |
881 |
|
883 |
887 |
907 |
911 |
919 |
929 |
937 |
941 |
|
947 |
953 |
967 |
971 |
977 |
983 |
991 |
997 |
