Файл: 3 зертханалы жмыс Пні Басару объектілерін моделдеу жне идентификациялау.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Коммерциялық емес акционерлік қоғам
«Ғұмарбек Дәукеев атындағы АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ»
«Автоматтандыру және басқару» кафедрасы
№3 зертханалық жұмыс
Пәні: «Басқару объектілерін моделдеу және идентификациялау»
Мамандығы: 6B07108 – «Автоматтандыру және басқару»
Орындаған: Серіков Алишер
Тобы: АУ(АИСУ)к-20-6
Нұсқа: №20
Тексерген: аға оқытушы Маркабаева Ж. С.
_____________ _____________ «___» ____________ 2022 ж.
(бағасы) (қолы)
3 Зертханалық жұмыс №3. Бірінші ретті сызықты объектілерін графикалық әдісімен идентификациялау
Жұмыс мақсаты: сызықты динамикалық объекттілерді өтпелі функция көмегімен идентификациялаудың әдістерін үйрену.
3.1 Зертханалық жұмысқа тапсырма
Зертханалық жұмысты жасау барысында студент келесі тапсырмаларды орындауы керек:
- бірінші ретті сызықты объектті графикалық идентификациялау әдістерін оқу[2,3];
- өтпелі функция көмегімен объектіні идентификациялауға блок-диаграмманы нұсқаға сәйкес жинаңыз. Тапсырма нұсқалары Objects3 папкадан таңдалады;
- объектінің беріліс функциясының параметрлерін идентификациялаудың графикалық әдісімен анықтаңыз;
- идентификация дәлдігін бағалаңыз.
3.2 Өтпелі функция көмегімен идентификациялау әдісі
Жүйенің сызықты моделінің параметрлерін (беріліс функциясын) анықтау үшін оның өтпелі функциясының графигін қолдануға болады. Бұл әдісті сызықты жүйелердің көбісіне қолдануға болады (1 және 2 ретті және жоғарғы ретті апериодикалық жүйелерге). Өтпелі функция көмегімен графикалық идентификациялау әдісі бірінші ретті объектілңрге жақсы дәлдікпен қолданылады.
Бірінші ретті объект қарастырылады. Осындай объекттер үшін ізделінетін теңдеуі келесідей:
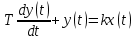 немесе
немесе 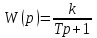 . (3.1)
. (3.1)Объектіде тәжірибелер өткізіледі: t0=0 уақыт моментінде кірістегі x мәні өзгеру жолмен a мәніне өзгереді және өтпелі процестің графикі жазылады. Осы графикті қолданып, беріліс функцияның T және k параметрлерін анықтау қажет.
(3.1) дифференциалдық теңдеудің жалпы шешімінің өрнегі келесі болады:
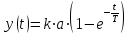 . (3.2)
. (3.2)(3.2) функциясы өтпелі процестің графигін сипаттайды. Қарапайымдау үшін а=1 қабылдаймыз.
Беріліс функцияның параметрлерін анықтау келесі жолдарымен орындауға болады:
а) (3.2) өрнектен
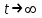 болғанда,
болғанда, 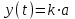 болатыны белгілі. Басқа жағынан
болатыны белгілі. Басқа жағынан 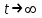 болғанда шығу сигналының тұрақтанған шамасын аламыз. Басқа сөзбен айтқанда объекттің орнықталған күйінің ординатасы арқылы k параметрін анықтауға болады (графикте).
болғанда шығу сигналының тұрақтанған шамасын аламыз. Басқа сөзбен айтқанда объекттің орнықталған күйінің ординатасы арқылы k параметрін анықтауға болады (графикте).t = T болғанда
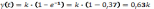
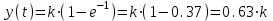 болады. Яғни бірінші ретті жүйенің T уақыт тұрақтысы өтпелі функция өзінің орнықталған шамасының 63% жеткендегі уақыт бөлігіне тең;
болады. Яғни бірінші ретті жүйенің T уақыт тұрақтысы өтпелі функция өзінің орнықталған шамасының 63% жеткендегі уақыт бөлігіне тең; б) k коэффициенті а) тарамындағыдай анықталады.
T параметрін анықтау үшін (3.2) өрнекті дифференциалдаймыз
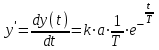 .
.Бастапқы нүктеде
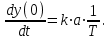
яғни (туындының геометриялық мағынасынан)
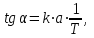
мұнда α – t = 0 функция графигіне болғанда жанаманың иілу бұрышы.
Басқа жағынан, жанама, абциссалар осі, жанамының орнықталған күйімен қиылысқан нүктесінен абциссалар осіне орнатылған перпендикуляр, тік бұрышты үшбұрышты құрайды; онда tgα– қарсы жатқанкатеттің іргелес жатқан катетіне қатынасы болып табылады. Яғни осы үшбұрышта іргелес жатқан катет T шамасы болады.
Сонымен,
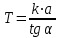 шамасы координаттар осінің басынан жанама асимптотамен қиылысатын нүктенің абсциссасына дейінгі аралық.
шамасы координаттар осінің басынан жанама асимптотамен қиылысатын нүктенің абсциссасына дейінгі аралық. Жұмысты орындалуы
- Simulink-тің модельдер редакторының ортасына Objects3 папкасынан өзіңіздің «объектіңізді» жүктеңіз (нұсқа бойынша). Порталдан Oblect3 папкасын жазып алып, өзімнің нұсқамды №18 таңдап алдым.
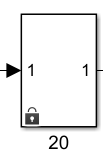
1 сурет – Нұсқа бойынша берілген объект
Кейін кіріс сигнал ретінде бірлік сатылы сигналды орнатып, шығыс сигналына Scope-ты беріп, терезесіне графикті шығарамыз.
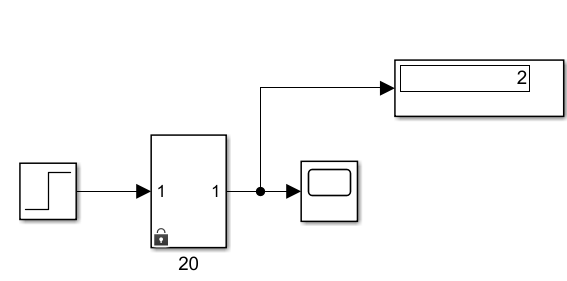
2 сурет – Кіріс/шығыс сигналын беру
Осы әрекеттер нәтижесінде «өлшеу стендтінің» блок-диаграммасын аласыз. Диаграмманы жұмысқа қосыңыз. Scope терезеде өтпелі процестің графигін аласыз - «тәжірибе» нәтижесі.
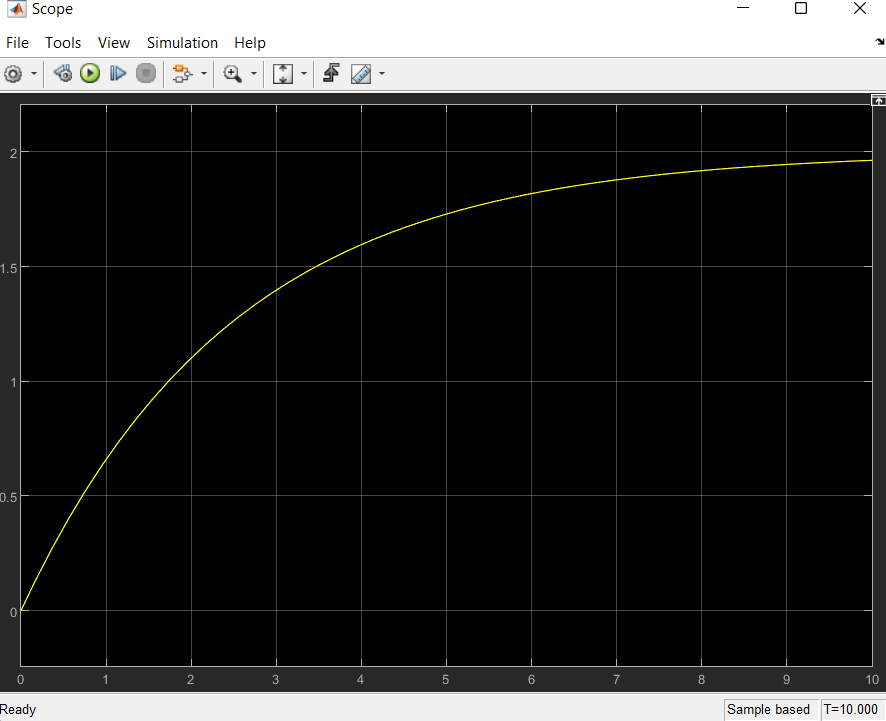
3 сурет – Объект графигі
Өтпелі процесс графигі бойынша орнықталған күйдің шамасын анықтаймыз, оны графикте K=2 екенін білеміз.
Дифференциалды теңдеу шешімінің жалпы (3.2) өрнегін қолдана, беріліс функцияның k беру коэффициентін анықтаңыз.
y(t) = k× (1- e-1 ) = k× (1- 0.37) = 0.63 × k
Бірінші ретті объектінің беріліс функцияның Т уақыт тұрақтысын екі амалмен (а және б) анықтаңыз. Жанаманы құруға Scope блоктың мүмкіншіліктерін қолданыңыз.
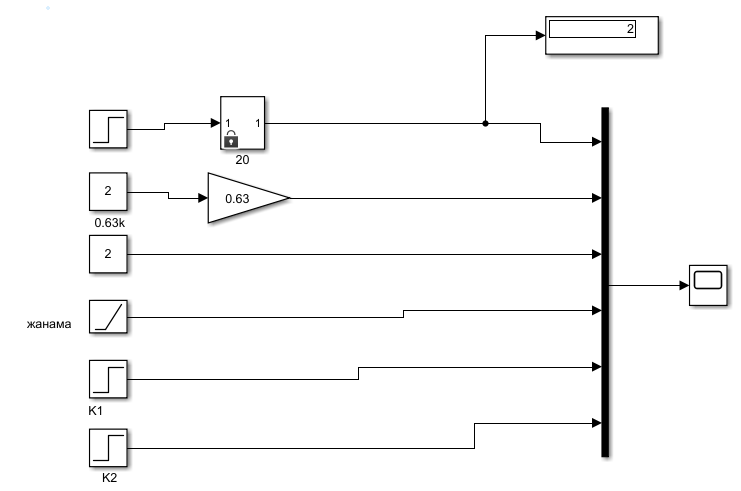
4 сурет – Уақыт тұрақтысын анықтау үшін құрылған модельдің блок-диаграммасы
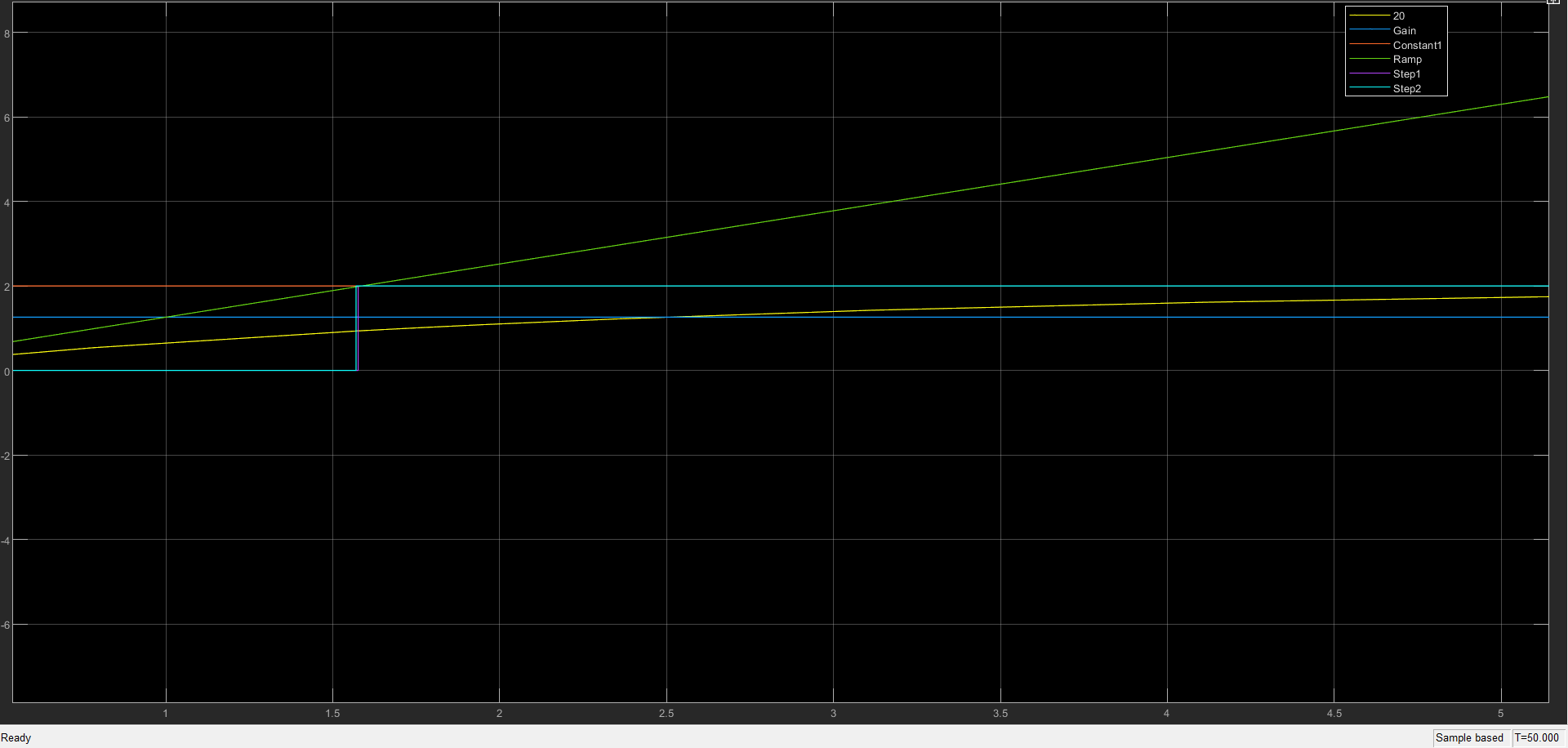
5 сурет – Объект параметрлерін анықтау
5 сурет арқылы T уақыт тұрақтысын 2 әдіс арқылы анықталынды:
а) жолы арқылы анықталған уақыт тұрақтысы T=2.469;
б) жолы арқылы анықталған уақыт тұрақтысы T=2.478 екені анықталды.
Нәтижесінде беріліс функциялар түріндегі екі модель пайда болады. Осы модельдердің өрнектерін жазыңыз.
Бірінші модель өрнегі:
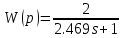
Екінші модель өрнегі:
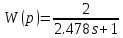
Transfer Function блогы көмегімен алынған модельдерді құрып, блок параметрлері терезесінде беріліс функцияның алымы мен бөлімінің коэффициенттерін орнатып аламыз.
«Объект» пен модельдер кірісіне бірдей сатылы сигналды орнатып, шығудағы сигналдарды аламыз.
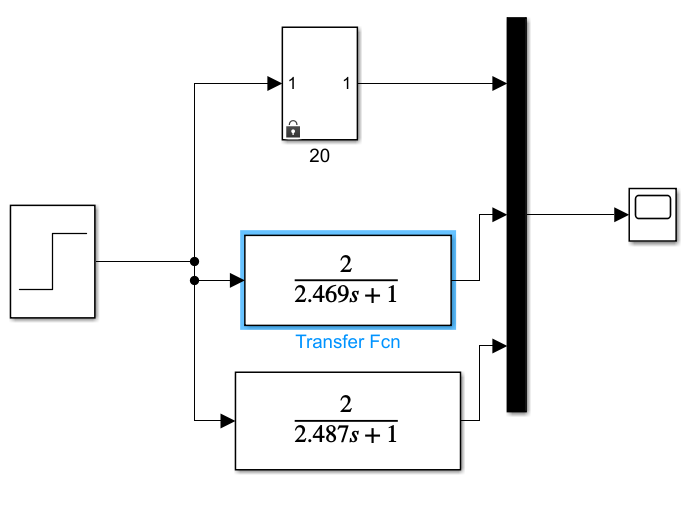
6 сурет – Объект пен моделдердің шығудағы сигналдарын салыстыру
блок-диаграммасы
«Объект» пен моделдер көмегімен алынған өтпелі процестердің графиктерін салыстырыңыз. Модельдердің дәлдігін бағалаңыз.
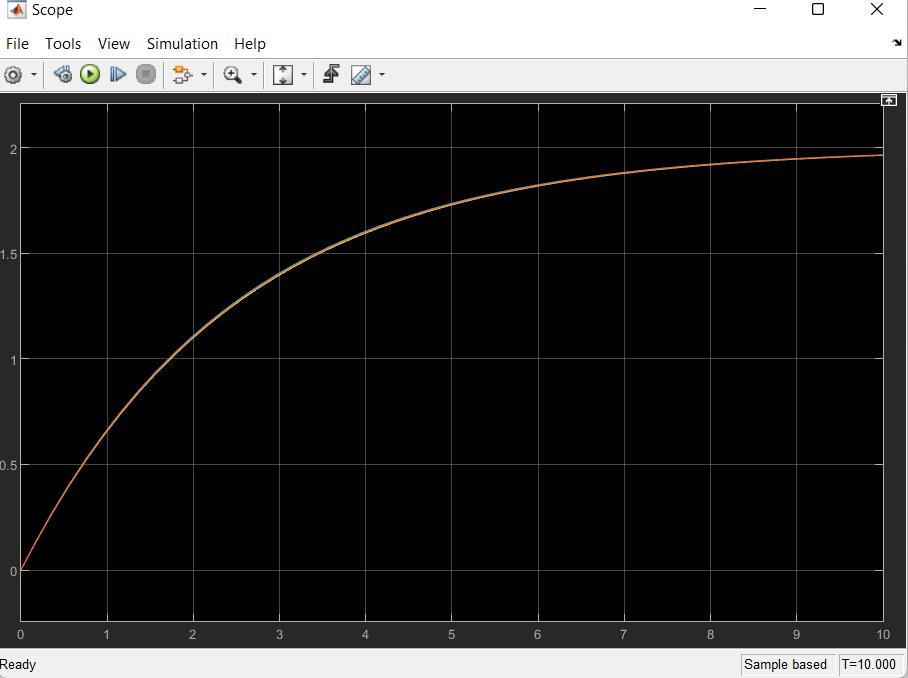
7 сурет – «Объект» және моделдер көмегімен алынған өтпелі процестер
Қорытынды
№ 3 зертханалық жұмыс бойынша MatLab жүйесінің Simulink пакетінде бірінші ретті сызықты объектілерін идентификациялаудың тура әдістерін қолдану барысындағы жұмыстар жүргізілді. Жұмыс негізінде өтпелі функция арқылы идентификациялау жүргізілді. Сондай-ақ, бірінші ретті сызықты объектті графикалық идентификациялау әдістерімен танысылды. Сонымен қатар, өтпелі функция көмегімен объектіні идентификациялауға блок-диаграммасы жиналды.
Жұмыста объекттің өтпелі сипаттамасының көмегімен жүйенің беріліс функциясы екі а) және б) жолымен анықталды. Содан кейін объект және модельдердің өтпелі сипаттамалары салыстырылды. Соның нәтижесінде а және б жолымен анықталған модельдің объект сипаттамасына сәйкес екені анықталды.
Алматы, 2023

