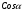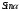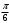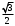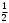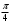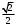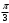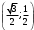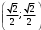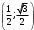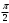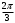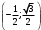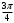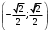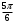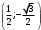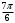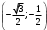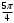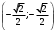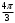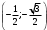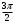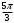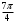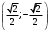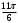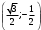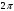ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.03.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Раздел: 9.3А | Тригонометрия. | |
| ФИО педагога: | Чебакова О.В. | |
| Дата: | 20.01.2021г. | |
| Класс: 7 | Количество присутствующих: | Количество отсутствующих: |
| Тема урока: | Тригонометрические функции и их свойства. | |
| Цель обучения в соответствии с учебной программой | 9.2.4.5 находить с помощью единичной окружности область определения и множество значений тригонометрических функций; | |
| Цель урока | Все находят область определения и множество значений тригонометрических функций с помощью единичной окружности. Большинство применяют знания о переводе градусной меры в радианную и наоборот. Некоторые применяют знания о преобразованиях графиков функций. | |
ХОД УРОКА
| Этапы урока/ время | Действия педагога | Действия ученика | Оценивание Рубрика | Ресурсы | ||||||||||||||||||||||||||||||||||||||||||||||
| Начало урока/ 5 мин | Приветствие- повторение. Актуализация знаний. Приложение 1. Индивидуальная работа. Поставьте баллы в лист оценивания. | Задают вопросы и получают ответы по темам прошлых уроков(перевод из градусной меры в радианную и наоборот, положительное и отрицательное направление поворота, определение тригонометрических функций, координаты точки на единичной окружности) При повороте точки Р на угол При повороте точки Р на угол При повороте точки Р на угол При повороте точки Р на угол | Одобрение учителя, и/или исправления учителя и учеников. Дескрипторы: 1б записывает координаты точки при повороте на 900 1б записывает координаты точки при повороте на минус 900 1б записывает координаты точки при повороте на 2700 1б записывает координаты точки при повороте на минус 1800 | Слайды с ответами и дескрипторами, карточки с заданием. Листы оценивания. | ||||||||||||||||||||||||||||||||||||||||||||||
| Середина урока/ 32 мин | Новая тема. Исследование. Рассмотрим единичную окружность. Повторим расположение углов поворота точки А(0;1) как в положительном , так и в отрицательном направлении, координаты точек, получающихся при поворотах. Работа в парах.(10 мин) 1. Чему равен косинус углов 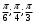 ? ?2. Чему равен синус углов 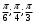 ? ?3. Сделайте вывод. 4. Записать координаты точек, получившихся при поворотах точки А(0;1) на углы 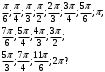 5. Какие углы можно отметить на единичной окружности? 6. Какой вывод вы можете сделать? 7. Какие значения принимают абсциссы(косинус) и ординаты(синус) точек на единичной окружности? 8. Какой вывод вы можете сделать? Обсудим ваши ответы. Задайте вопросы. Поставьте баллы в лист оценивания. Групповая работа.(5 мин) С первых парт повернитесь ко вторым, с третьих повернитесь к четвёртым партам. Получилось 6 групп по 4 человека. Обсудите вместе и решите: каковы же область определения и множество значений тангенса и котангенса? Проверим ваши выводы. Поставьте баллы в лист оценивания. Работа в группах .(5 мин) Оформим таблицу: Проверим. Поставьте баллы в лист оценивания. Работа в парах.(5 мин) Найдите область определения и множество значений функций: 1. y=Sin 3x 2. y=Cos 2x+5 3. 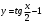 4. 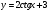 Проверим решение. Поставьте баллы в лист оценивания. | 1. 2.
3. 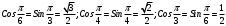 4.
5. Сколь угодно большие и сколь угодно малые. 6. Область определения синуса и косинуса есть любое число. 7. От 0 до 1. 8. Множество значений синуса и косинуса от минус 1 до 1 включительно. Так как 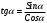 , то Cos , то Cos  не может быть равным нулю. не может быть равным нулю.Значит из всех значений надо убрать углы, при которых косинус равен нулю. То есть 900, 2700, такие же отрицательные и учесть повторение значений при совершении оборотов. Так как 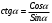 , Sin , Sin  не может равняться нулю. И из всех значений надо убрать углы, при которых синус равен нулю. Это 00, 1800 и противоположные им углы. Надо учесть, что при совершении оборотов получаются те же значения. не может равняться нулю. И из всех значений надо убрать углы, при которых синус равен нулю. Это 00, 1800 и противоположные им углы. Надо учесть, что при совершении оборотов получаются те же значения.Множество значений этих функций будет любое число, так как в числителе и знаменателе дробей 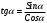 и и 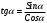 будут числа от минус единицы до плюс единицы. будут числа от минус единицы до плюс единицы. 1. D (Sin 3x)=R, E(Sin 3x)= [-1;1] 2. D (Cos 2x +5)=R, E(Cos 2x+5)=[-4;6] 3. 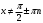 , E(y)=R , E(y)=R4. 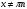 , E(y)=R , E(y)=R | Дескрипторы: 1б записывает значения косинуса 300 и синуса 600 1б записывает значения синуса и косинуса 450 1б записывает значения косинуса 600 и синуса 300 1б записывает равенство значений косинуса 300 и синуса 600 1б записывает равенство значений синуса и косинуса 450 1б записывает равенство значений косинуса 600 и синуса 300 16 баллов записывает координаты точек на единичной окружности 1б записывает, что угол любой величины можно изобразить на единичной окружности 1б записывают, что область определения синуса и косинуса есть любое число 1б записывают отрезок, в котором лежат все значения абсцисс и ординат точек 1б записывают, что множество значений синуса и косинуса есть отрезок от минус одного до одного. Дескрипторы: 1б применяют формулу 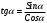 1б делают вывод: косинус не равен нулю 1б выбирают углы 900, 2700 по единичной окружности 1б добавляют противоположные им углы 1б учитывают полные обороты 1б применяют формулу 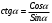 1б делают вывод: синус не равен нулю 1б выбирают углы 00, 1800 на единичной окружности 1б добавляют противоположные им углы 1б учитывают полные обороты 1б применяют знания о множествах значений синуса и косинуса 1б записывают множества значений тангенса и котангенса 1б участие в работе группы 1б активное участие в работе группы 1б лидер группы Дескрипторы: 1б предлагает запись областей определения синуса и косинуса и множеств значений тангенса и котангенса от минус бесконечности до плюс бесконечности или множество всех действительных чисел 1б предлагает запись множеств значений синуса и косинуса в виде двойного нестрогого неравенства или в виде отрезка 1б предлагает запись области определения тангенса в виде 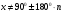 или или 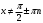 , где n – целое число , где n – целое число1б предлагает запись области определения котангенса в виде 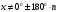 или или 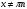 , где , где 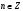 . .Дескрипторы: 1б записывает D (Sin 3x)=R 1б записывает E(Sin 3x)= [-1;1] 1б записывает D (Cos 2x +5)=R 1б применяет E(Cos x)=[-1;1] 1б записывает E(Cos 2x+5)=[-4;6] 1б записывает 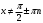 1б записывает E(y)=R 1б записывает 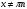 1б записывает E(y)=R | Слайды презентации с пояснительными рисунками, решениями и дескрипторами Карточки с заданиями, тригонометрическим кругом, таблицами для заполнения. Приложение 2. Приложение 3. Слайды презентации с решениями и дескрипторами. Карточки с таблицей для заполнения. Приложение 4. Слайды презентации с решениями и дескрипторами. Карточки с заданием. Приложение 5. Слайды презентации с решениями и дескрипторами. | ||||||||||||||||||||||||||||||||||||||||||||||
| Конец урока/ 3 мин | Посчитайте сумму баллов и проценты. Вы довольны результатом? Поднимите смайлики настроения. Посмотрите на домашнее задание. Задайте вопросы. | Домашнее задание. Найдите область определения и множество значений функций: 1. y= Sin 3x -1 2. у=3Cos 4x+1 3. у= 5+ tg 2x 4. у= 2-3ctg (x/2) | | Карточки с домашним задание каждому. Приложение 6. |
П
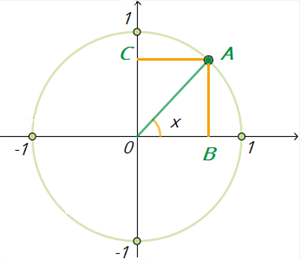 риложение 1. Индивидуальная работа.
риложение 1. Индивидуальная работа.Какая точка получится при повороте точки Р(1; 0) на угол
П
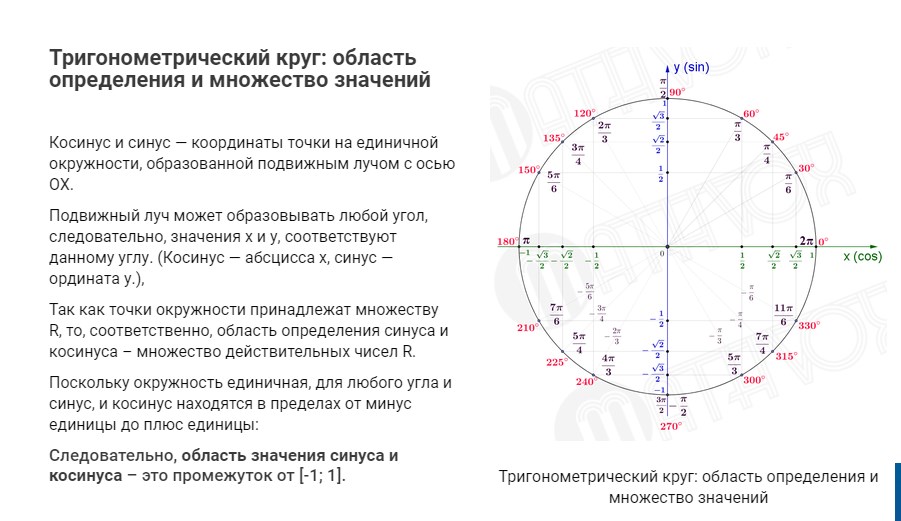 риложение 2. Тригонометрический круг
риложение 2. Тригонометрический круг Приложение 3. К групповой работе (10 мин)
 | 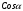 | 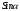 |
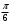 | | |
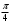 | | |
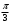 | | |
| угол | координаты |
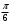 | |
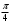 | |
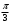 | |
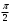 | |
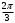 | |
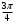 | |
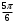 | |
 | |
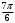 | |
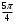 | |
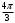 | |
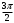 | |
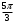 | |
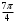 | |
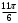 | |
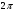 | |
Приложение 4. Групповая работа (5 мин)
| Функция | Область определения D(y) | Область значений E(y) |
| y=Sin x | | |
| y= Cos x | | |
| y= tg x | | |
| y= ctg x | | |
Приложение 5. В парах (5 мин)
Найдите область определения и множество значений функций:
1. y=Sin 3x
2. y=Cos 2x+5
3.
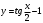
4.
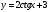
Приложение 6. Домашнее задание.
Найдите область определения и множество значений функций:
1. y= Sin 3x -1
2. у=3Cos 4x+1
3. у=5+ tg 2x
4. у= 2-3ctg (x/2)
Лист оценивания.
| Этапы урока | Критерий оценивания/дескрипторы | Максимальное количество баллов | Получено |
| Начало урока Индивидуальная работа | Дескрипторы: 1б записывает координаты точки при повороте на 900 1б записывает координаты точки при повороте на минус 900 1б записывает координаты точки при повороте на 2700 1б записывает координаты точки при повороте на минус 1800 | 4 | |
| Середина урока Работа в парах. (10 мин) Групповая работа. (5 мин) Групповая работа. (5 мин) Работа в парах. (5 мин) | Дескрипторы: 1б записывает значения косинуса 300 и синуса 600 1б записывает значения синуса и косинуса 450 1б записывает значения косинуса 600 и синуса 300 1б записывает равенство значений косинуса 300 и синуса 600 1б записывает равенство значений синуса и косинуса 450 1б записывает равенство значений косинуса 600 и синуса 300 16 баллов записывает координаты точек на единичной окружности 1б записывает, что угол любой величины можно изобразить на единичной окружности 1б записывают, что область определения синуса и косинуса есть любое число 1б записывают отрезок, в котором лежат все значения абсцисс и ординат точек 1б записывают, что множество значений синуса и косинуса есть отрезок от минус одного до одного Дескрипторы: 1б применяют формулу 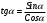 1б делают вывод: косинус не равен нулю 1б выбирают углы 900, 2700 по единичной окружности 1б добавляют противоположные им углы 1б учитывают полные обороты 1б применяют формулу 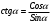 1б делают вывод: синус не равен нулю 1б выбирают углы 00, 1800 на единичной окружности 1б добавляют противоположные им углы 1б учитывают полные обороты 1б применяют знания о множествах значений синуса и косинуса 1б записывают множества значений тангенса и котангенса 1б участие в работе группы 1б активное участие в работе группы 1б лидер группы Дескрипторы: 1б предлагает запись областей определения синуса и косинуса и множеств значений тангенса и котангенса от минус бесконечности до плюс бесконечности или множество всех действительных чисел 1б предлагает запись множеств значений синуса и косинуса в виде двойного нестрогого неравенства или в виде отрезка 1б предлагает запись области определения тангенса в виде 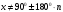 или или 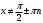 , где n – целое число , где n – целое число1б предлагает запись области определения котангенса в виде 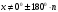 или или 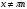 , где , где 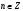 . .Дескрипторы: 1б записывает D (Sin 3x)=R 1б записывает E(Sin 3x)= [-1;1] 1б записывает D (Cos 2x +5)=R 1б применяет E(Cos x)=[-1;1] 1б записывает E(Cos 2x+5)=[-4;6] 1б записывает 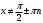 1б записывает E(y)=R 1б записывает 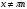 1б записывает E(y)=R | 26 15 4 9 | |
| Итого: | | 54 | |
| Проценты: | | 100 | |
Область определения тригонометрических функций - поиск Яндекса по видео (yandex.kz)