Файл: Алгебра Таким образом, если число оканчивается на 0, 2, 4, 6, 8 оно без остатка делится на 2.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Алгебра
1. Таким образом, если число оканчивается на 0, 2, 4, 6, 8 - оно без остатка делится на 2. Признак делимости на 5: на 5 без остатка делится число, оканчивающееся на 5 или 0. Признак делимости на 10: на 10 без остатка делится число, оканчивающееся на 0. Признак делимости на 3 и 9. Если делимость на 2, 5 и 10 устанавливают по последней цифре делимого, то делимость на 3 и 9 устанавливают по сумме всех цифр делимого.
2. При записи числовых неравенств используются следующие знаки:
<, a
>, a>b — a больше b
≠, a≠b — a не равно b
Основные свойства числовых неравенств Свойство 1. Если а>b и b >с, то а >с. Свойство 2. Если а>b, то a+c>b+c. Если к обеим частям неравенства прибавить одно и тоже число, то знак неравенства не изменится. Следствие (из свойства 2). Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный. а+с < b а < b-с. Свойство 3. Если a>b, m>0, то am>bm.
3. Формулы сокращенного умножения

4. Свойства линейной функции. 1) Область определения функции - множество всех действительных чисел 2) Множеством значений функции является множество всех действительных чисел 3) Функция не имеет ни наибольшего, ни наименьшего значений. 4) Функция не является ни четной, ни нечетной (кроме особых случаев). 5) Функция непериодическая. 6) График функции пересекает ось Ох в точке, а ось Оу - в точке (0; b). 7) - является нулем функции.
Графиком линейной функции является прямая. Если k = 0, то функция y = b называется постоянной. Её графиком, является прямая, параллельная оси Ox. Если b = 0, то формула y = kx задает прямо пропорциональную зависимость. Графиком такой функции является прямая, проходящая через начало координат. Верно и обратное - любая прямая, не параллельная оси Oy, является графиком некоторой линейной функции.
5. Корни квадратного уравнения вычисляют по формулам:




6. Квадратичной (квадратной) функцией называется функция вида где a, b, с - числа. Графиком квадратичной функции является парабола. Парабола имеет вершину, ось, проведенная через вершину и параллельная оси Оу, делит параболу на две симметричные части. Вершиной параболы называется точка. Если коэффициент а>0, то ветви параболы направлены вверх, если a<0, то ветви параболы направлены вниз.
Свойства квадратичной функции y=x 2 1). Областью определения функции является множество всех действительных чисел, т.е. 2). Множеством значений функции является промежуток 3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет. 4) Функция является четной, график симметричен относительно оси Оу. 5) Функция непериодическая. 6)Парабола имеет с осями координат единственную общую точку (0; 0) - начало координат.
7. Неравенство Коши о среднем арифметическом и среднем геометрическом
Неравенство
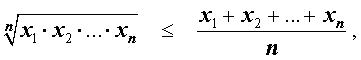
утверждающее, что среднее геометрическое n положительных чисел не превосходит их среднего арифметического, называется неравенством Коши.
В случае, когда n = 2 , неравенство Коши имеет вид
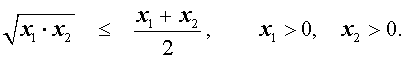
Докажем это неравенство:
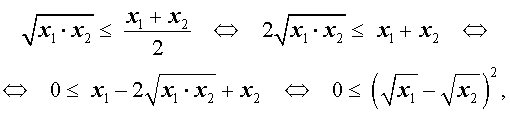
что и требовалось.
Из неравенства Коши с n = 2 , взяв
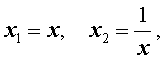
нетрудно получить очень полезное следствие.
Следствие. Для произвольного положительного числа x выполнено неравенство
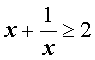
1. Неравенство о сумме двух взаимно обратных чисел:
1) Если a > 0 , то справедливо неравенство a + (1/a) ≥ 2,
причём неравенство обращается в равенство только при a = 1.
2) Если a < 0 , то справедливо неравенство a + (1/a) ≤ −2,
причём неравенство обращается в равенство только при a = −1.
Следствие. Если a и b – два числа одного знака, т.е. ab > 0, то справедливо неравенство а/b + b/а ≥ 2.
8. Арифметическая прогрессия


8. Геометрическая прогрессия



10.
Свойства степеней с натуральными показателями
По определению степени с натуральным показателем степень an представляет собой произведение n множителей, каждый из которых равен a. Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел, можно получить и обосновать следующие свойства степени с натуральным показателем:
-
основное свойство степени am·an=am+n, его обобщение an1·an2·…·ank=an1+n2+…+nk; -
свойство частного степеней с одинаковыми основаниями am:an=am−n; -
свойство степени произведения (a·b)n=an·bn, его расширение (a1·a2·…·ak)n=a1n·a2n·…·akn; -
свойство частного в натуральной степени (a:b)n=an:bn; -
возведение степени в степень (am)n=am·n, его обобщение (((an1)n2)…)nk=an1·n2·…·nk; -
сравнение степени с нулем:
-
если a>0, то an>0 для любого натурального n; -
если a=0, то an=0; -
если a<0 и показатель степени является четным числом 2·m, то a2·m>0, если a<0 и показатель степени есть нечетное число 2·m−1, то a2·m−1<0;
если a и b – положительные числа и ann;
если m и n такие натуральные числа, что m>n, то при 0mn, а при a>0 справедливо неравенство am>an.
Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an.
Свойства степеней с целыми показателями
Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.
Степень с целым отрицательным показателем, а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.
Итак, для любых действительных и отличных от нуля чисел a и b, а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями:
-
am·an=am+n; -
am:an=am−n; -
(a·b)n=an·bn; -
(a:b)n=an:bn; -
(am)n=am·n; -
если n – целое положительное число, a и b – положительные числа, причем ann и a−n>b−n;
если m и n – целые числа, причем m>n, то при 0mn, а при a>1 выполняется неравенство am>an.
При a=0 степени am и an имеют смысл лишь когда и m, и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0, а числа m и n – целые положительные.
Свойства степеней с рациональными показателями
Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:
-
свойство произведения степеней с одинаковыми основаниями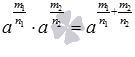 при a>0, а если
при a>0, а если 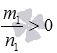 и
и 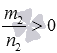 , то при a≥0;
, то при a≥0; -
свойство частного степеней с одинаковыми основаниями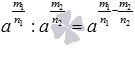 при a>0;
при a>0; -
свойство произведения в дробной степени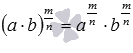 при a>0 и b>0, а если
при a>0 и b>0, а если 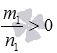 и
и 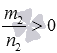 , то при a≥0 и (или) b≥0;
, то при a≥0 и (или) b≥0; -
свойство частного в дробной степени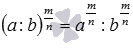 при a>0 и b>0, а если
при a>0 и b>0, а если 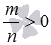 , то при a≥0 и b>0;
, то при a≥0 и b>0; -
свойство степени в степени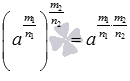 при a>0, а если
при a>0, а если 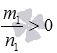 и
и 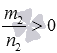 , то при a≥0;
, то при a≥0; -
свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b, a0 справедливо неравенство app, а при p<0 – неравенство ap>bp;
свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q, p>q при 0pq, а при a>0 – неравенство ap>aq.
Определение корня n-й степени
Корнем
Например, корнем
Если
Если
Если
Арифметическим корнем
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень той же степени. Например,
Если
Если
Если
При всех значениях имеющего смысл выражения
Если
Пример 1:
Если
11.
Степенная функция с целым показателем



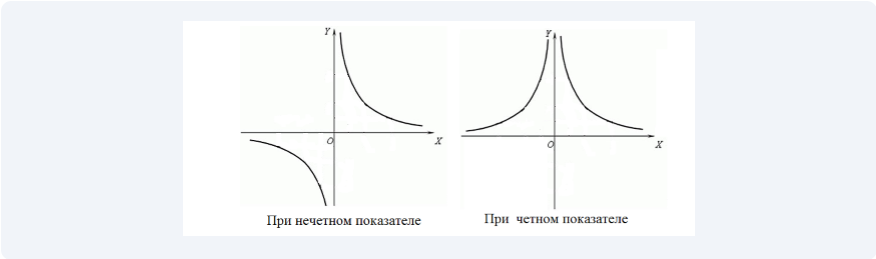
12.
Показательная функция, её график и свойства
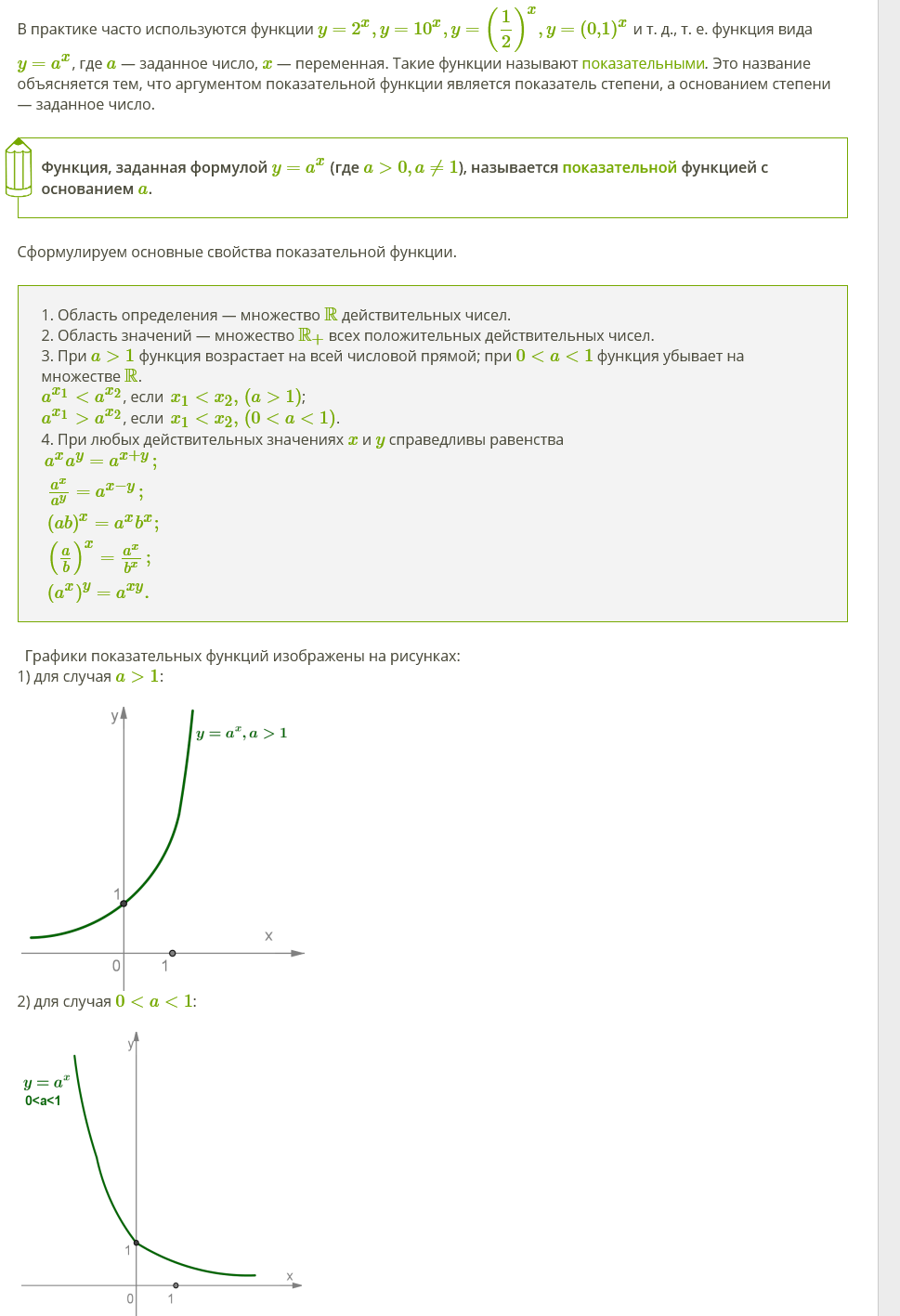
13.
Основное логарифмическое тождество
Логарифм числа b по основанию a является обратной функцией показательного уравнения b = a x.
Пишется как log a b = x и означает следующее: в какую степень x нам нужно возвести число a, чтобы получить b.
При этом:
-
основание a должно быть положительным числом, не равным единице (a>0, a≠1); -
число b должно быть положительным (b>0), т.к. при отрицательном значении корня уравнения (x) не существует (при положительном – корень один).
Формула основного логарифмического тождества
Если перечисленные выше условия выполняются, то справедливо следующее выражение, которое имеет специальное название – основное логарифмическое тождество:
a log a b = b
Следствие:
Если log a b = log a c, то a log a b = a log a c. А значит, b = c.






14.
Логарифмическая функция, её свойства и график
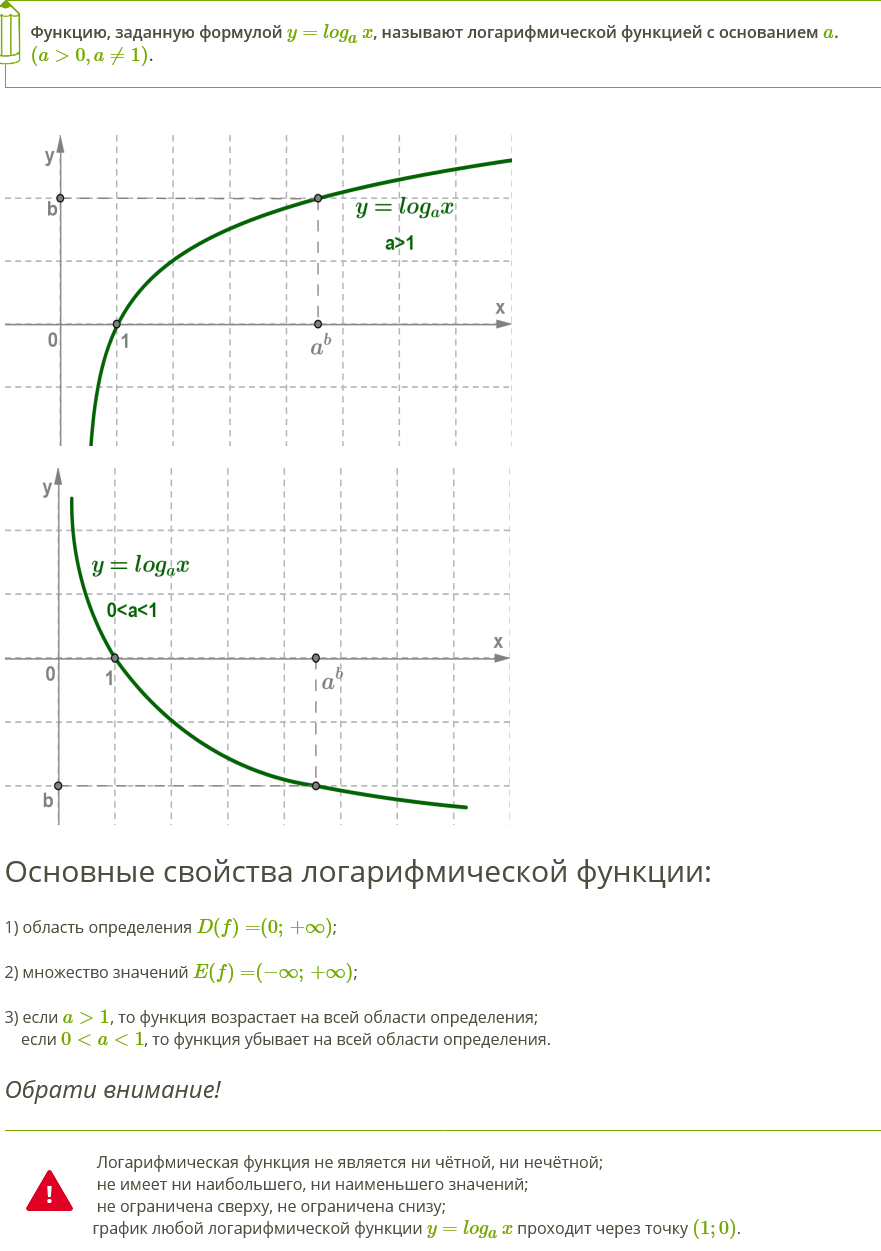
1>0>1>1>0>0>

