6. Простые и сложные события. Сумма событий. Теорема сложения вероятностей.

Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.

Если A и B - совместные события, то суммой 2ух событий A и B называется событие С, состоящее в наступлении либо события A, либо события B, либо обоих событий вместе. Если A и B - несовместные события, то их сумма означает наступление или события A, или соб. B.

Теорема сложения вероятностей.

Вероятность суммы 2х событий равна сумме вероятностей этих событий без вероятности их совместного наступления.



Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий:

P(A+B+....+K)=P(A)+P(B)+....+P(K)

Следствие 1. Сумма вероятностей событий, образующих полную группу равна единице.

, где А1,А2..An-полная группа событий

Следствие 2. Сумма вероятностей противоположных событий равна единице.

7. Простые и сложные события. Произведение событий. Условная вероятность события. Теорема умножения вероятностей.

Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.

Условная вероятность события B - это полученная вероятность события B, найденная при условии, что событие A произошло. Обозначается  (B) или P(B/A)

Теорема умножения вероятностей.

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.

Теорема умножения для несовм.событий

Вероятность произведения независимых событий равна произведению вероятностей этих событий

---

A и B-независимые.

8. Формула Бернулли. Формула Пуассона. Сфера их применения.

Формула Бернулли

Т-ма: Если вероятность p наступления события A в каждом испытании постоянна, то вероятность P k,n того, что событие А наступит k раз в n независимых испытаниях равна:



где q = 1-p

В формуле Бернулли используется число сочетаний. Для реализации схемы Бернулли необходимы два условия: 1) независимость проводимых испытаний; 2) p = const Распределение вероятностей в схеме Бернулли - биномиальное.

Применяется при решении задач на нахождение вероятности возможного числа появления бракованных деталей; в задаче с условием найти количество подбросов игральной кости, при заданном наивероятнейшем выпадении

Формула Пуассона

Применяется в случае, когда мы хотим вычислить вероятность Pm,n появления события A при большом числе испытаний n, например P300,500.

Т-ма: Если вероятность p наступления события А в каждом испытании стремится к нулю при неограниченном увеличении числа n испытаний, причем произведение np стремится к постоянному числу λ, то вероятность Pm,n того, что событие A появится m раз в n независимых испытаниях, удовлетворяет предельному равенству



Приближенная формула Пуассона:



9. Локальная и интегральная теоремы Муавра-Лапласа.

Локальная Теорема.

Если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и 1,то вероятность P(m,n) того, что событие А произойдет m раз в n независимых испытаниях при n достаточно больших, приближенно равна  ; g=1-р



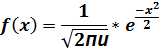
Существует таблица значений функций f(x)для x

---

[0;5] при x >=5 f(x)



Интегральная теорема.

Если вероятность P наступления события A в отдельных испытаниях постоянна и отлично от 0 и 1, то вероятность того, что число m наступления события A в n Независимых испытаниях заключено в пределах от A до B включительно при достаточно большом числе испытаний n приблизительно равна 



Следствие. Если вероятность P наступления события А в отдельных испытаниях постоянна и отлична от 0 до 1, то при достаточно большом числе n независимых испытаний вероятность того что,

а) число m наступления события А отличается от произведения np не более чем на величину E>0 приближенна равна p(

б)Частота   события А в n независимых испытаниях заключена в пределах от α До β включительно приближенна равна P(α

z1= ; z2= 

В) частота   отличаются от вероятности (p) его наступления в отдельном испытании на величину ∆≥0 по абсолютной величине приближенно равна  )

---

10. Формула полной вероятности. Формула Байеса

Теорема. Если событие А может наступить только совместно с одним из событий (гипотез) Н1,Н2,…,Нn, образующих полную группу, то вероятность события А равна

Р(А  =>

 формула Байеса

---

Смотрите также файлы

• азаты салтдстрімен таныстыру. Бесік жыры жне тсау кесер жырымен таныстыру.docx

• Методические рекомендации для студентов, обучающихся по программе магистратуры, по написанию выпускной квалификационной работы.docx

• 1. Управление позволяет создавать соответствующие ожиданиям клиентов продукты и услуги в срок с минимальными затратами (качеством) Таргетированная атака.docx

• Теоретические основы учета финансовых результатов 5 1 Сущность и понятие финансовых результатов 5.docx

• Блім.docx