Файл: Построение и исследование имитационной модели вычислительной системы на основе событийного способа имитации.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 40
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
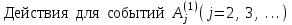
-
Увеличение числа поступивших заявок: .
. -
Проверка состояния канала:
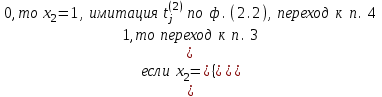
-
Проверка состояния накопителя:
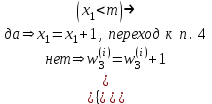
-
Имитация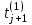 по формуле (2.2).
по формуле (2.2). -
Вычисление момента t(r+1) наступления будущего события по формуле (2.1)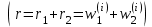 .
. -
Определение типа будущего события α(r+1) по формуле (2.3). -

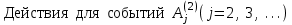
-
Увеличение числа обслуженных заявок: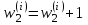 .
. -
Проверка состояния накопителя:
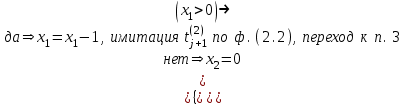
-
Вычисление момента t(r+1) наступления будущего события по формуле (2.1)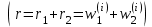 .
. -
Определение типа будущего события α(r+1) по формуле (2.3). -

Замечание. При выполнении п. 3 может оказаться, что переменная
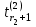 в формуле (2.3) не определена (х1 = х2 = 0). В подобных случаях целесообразно полагать
в формуле (2.3) не определена (х1 = х2 = 0). В подобных случаях целесообразно полагать 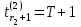 .
.Действия для события А(3).
Событие "завершение моделирования" требует специальных действий, связанных с увеличением интервала моделирования [0, T] на величину Δτ, необходимую для завершения обслуживания заявки, находящейся в канале обслуживания (если таковая в момент Т модельного времени имеется), и предотвращением поступления новых заданий. Последнее достигается переходом к обработке и выводу новых результатов. Поэтому последовательность действий для А(3) следующая.
-
Проверка состояния канала:
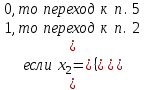
-
Увеличение числа обслуженных заявок: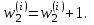
-
Переход канала из занятого состояния в свободное: х2 = 0. -
Увеличение интервала моделирования на величину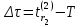 .
. -
Вывод результатов i-го прогона ИМ: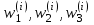 .
.
Пример. Пусть m = 1 и в результате имитационного моделирования рассматриваемой системы S на интервале [0, Т] для i-го прогона получена последовательность событий, изображенная на временной диаграмме (рис. 2). Тогда в результате выполнения описанных выше последовательностей действий будут получены фазовая траектория:
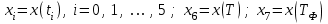
и показатели эффективности, приведенные в табл. 1.
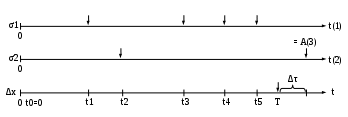
Рис. 2. Временная диаграмма последовательности событий
Таблица 1. Значения показателей эффективности системы в примере
| Переменные | t0 | t1 | t2 | t3 | t4 | t5 | t6 | t7 |
| x1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| x2 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
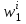 | 0 | 1 | 1 | 2 | 3 | 4 | 4 | 4 |
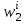 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 |
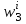 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
Этап 3. Разработка и исследование имитационной модели вычислительной системы
Постановка задачи
1. Разработать программу, имитирующую функционирование простейшей вычислительной системы с помощью изученного языка программирования.
2. Провести исследования с помощью разработанной имитационной модели по результатам нескольких прогонов.
Исходные данные для моделирования приведены в таблице № 2 согласно номерам общего списка студентов группы в журнале.
3. Обработать результаты моделирования, рассчитав выборочные средние и выборочные дисперсии следующих шести показателей эффективности:
-
среднее число поступивших в систему заявок; -
среднее число обслуженных заявок; -
среднее число потерянных заявок; -
статистическая вероятность обслуживания задания; -
статистическая вероятность отказа в обслуживании задания; -
среднее время простоя процессора.
Выборочное среднее значение показателя эффективности вычисляется по результатам n прогонов имитационной модели на интервале моделирования [0; T] по формуле:
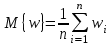
где wi – значение показателя эффективности, полученное по результату i-го прогона имитационной модели.
Для вычисления выборочной дисперсии необходимо использовать формулу:
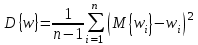
Содержание отчета по контрольной работе:
1. Тема и цель контрольной работы.
2. Исходные данные по вашему варианту (написать его номер).
3. Текст созданной программы для имитации работы исследуемой системы.
4. Скриншоты результатов вычисления шести показателей эффективности системы.
5. Выводы по работе с учетом полученных результатов исследования модели системы (недостатки исследованной модели, ваши предложения по ее модернизации и т.д.).
Так как на защиту контрольной работы аудиторное время не выделяется, то защиту планировать с распечатанной работой во время защиты лабораторных работ и решений практических занятий.
Таблица 2. Варианты исходных данных для моделирования ИМ простейшей вычислительной системы.
| Вариант (по общему списку группы) | l | m | T | m | Число прогонов |
| 1 | 0,2 | 0,15 | 180 | 30 | 120 |
| 2 | 0,3 | 0,25 | 270 | 20 | 85 |
| 3 | 0,25 | 0,2 | 190 | 40 | 90 |
| 4 | 0,35 | 0,3 | 210 | 50 | 140 |
| 5 | 0,15 | 0,12 | 260 | 25 | 100 |
| 6 | 0,4 | 0,33 | 175 | 18 | 130 |
| 7 | 0,45 | 0,4 | 300 | 45 | 125 |
| 8 | 0,22 | 0,2 | 280 | 30 | 145 |
| 9 | 0,32 | 0,3 | 260 | 42 | 90 |
| 10 | 0,27 | 0,23 | 195 | 28 | 100 |
| 11 | 0,18 | 0,15 | 230 | 35 | 80 |
| 12 | 0,27 | 0,21 | 185 | 42 | 75 |
| 13 | 0,41 | 0,36 | 210 | 25 | 90 |
| 14 | 0,35 | 0,31 | 175 | 38 | 105 |
| 15 | 0,12 | 0,1 | 220 | 40 | 95 |
| 16 | 0,23 | 0,19 | 190 | 53 | 110 |
| 17 | 0,31 | 0,24 | 290 | 20 | 80 |
| 18 | 0,19 | 0,16 | 300 | 35 | 90 |
| 19 | 0,4 | 0,34 | 270 | 45 | 135 |
| 20 | 0,26 | 0,23 | 195 | 50 | 115 |
| 21 | 0,38 | 0,31 | 230 | 25 | 120 |
| 22 | 0,17 | 0,15 | 285 | 30 | 100 |
| 23 | 0,42 | 0,39 | 180 | 40 | 95 |
| 24 | 0,11 | 0,1 | 265 | 35 | 125 |
| 25 | 0,32 | 0,29 | 320 | 55 | 85 |
| 26 | 0,29 | 0,23 | 275 | 20 | 95 |
| 27 | 0,41 | 0,35 | 325 | 35 | 110 |
| 28 | 0,19 | 0,13 | 270 | 45 | 135 |
| 29 | 0,3 | 0,26 | 195 | 20 | 140 |
| 30 | 0,25 | 0,21 | 235 | 40 | 125 |

