ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| | |

Содержани
Задание 3
Задание 1 5
Задание 2 10
Задание 3 13
Задание 4 14
Заключение 20
Задание 3
Задание 1 5
Задание 2 9
Задание 3 13
Задание 4 15
Заключение 20
Список использованной литературы 20
Задание
1. Выполнить теоретический расчет фильтра (Табл. 1) в соответствии с методическими указаниями (2020г. выпуска) к лабораторной работе № 6.
Таблица 1
| Вариант | Тип КИХ-фильтра | Максимальное затухание в полосе пропускания | Минимальное затухание в полосе задерживания | Частота среза | Граничная частота зоны затухания |
| 2 | ФВЧ | 1,0 дБ | 80 дБ | 800 Гц | 600 Гц |
1.1 Выполнить расчет оптимальной частоты дискретизации, исходя из заданных параметров фильтра.
1.2 Нарисовать структуру, АЧХ спроектированного фильтра.
1.3 Рассчитать коэффициенты фильтра. Смоделировать фильтр в матлабе.
1.4 Провести анализ ошибки АЧХ зоны работы фильтра при переходе от коэффициентов с плавающей точкой к целочисленным 8-ми, 16-ти и 32-х разрядным. Привести графики ошибок.
1.5. Описать процедуру интеграции коэффициентов фильтра в среду микроконтроллера.
2. Реализовать код программы, выполняющий цифровую фильтрацию, в соответствии с заданием, для микроконтроллеров семейства PIC32MZ.
2.1 Привести блок-схему программы.
2.2 Привести листинг программы.
3. Выполнить экспериментальные исследования с лабораторным стендом по курсу МиМвСУ.
3.1 Привести блок схему подключения аппаратуры.
3.2 Задавая равномерной шкалой частот на генераторе, в соответствии с АЧХ фильтра по заданию,
снять экспериментальную АЧХ реально работающего цифрового фильтра. Представить график
экспериментально снятого АЧХ.
3.3 Представить фото собранного лабораторного стенда, во время выполнения экспериментов,
график входного и выходного сигналов на экране осциллографа при одном значении частоты.
4. Выполнить процедуру передискретизации предполагаемого исследуемого сигнала, согласно
заданному выходному потоку данных.
4.1 Рассчитать частоту выходного потока по формуле: ???????????????? = ???? ∗
????1/????2, где N1 – «7» позиция № зачетной книжки; где N2 – «8» позиция № зачетной книжки. Если параметр (N1, либо N2) равен нулю,
то принять его равным единице.
4.2 Разработать блок схему процедуры преобразования частоты дискретизации с применением
операций интерполяции и децимации.
4.3 Описать последовательность действий с подробным описанием всех процедур.
Задание 1
1.1. Оптимальная частота дискретизации выбирается в 4-10 раз больше максимальной частоты границ фильтра:
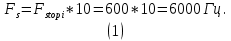
Частота Найквиста в этом случае будет равна:
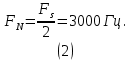
1.2. Структура и АЧХ спроектированного фильтра представлены на Рис. 1 и 2, соответственно.
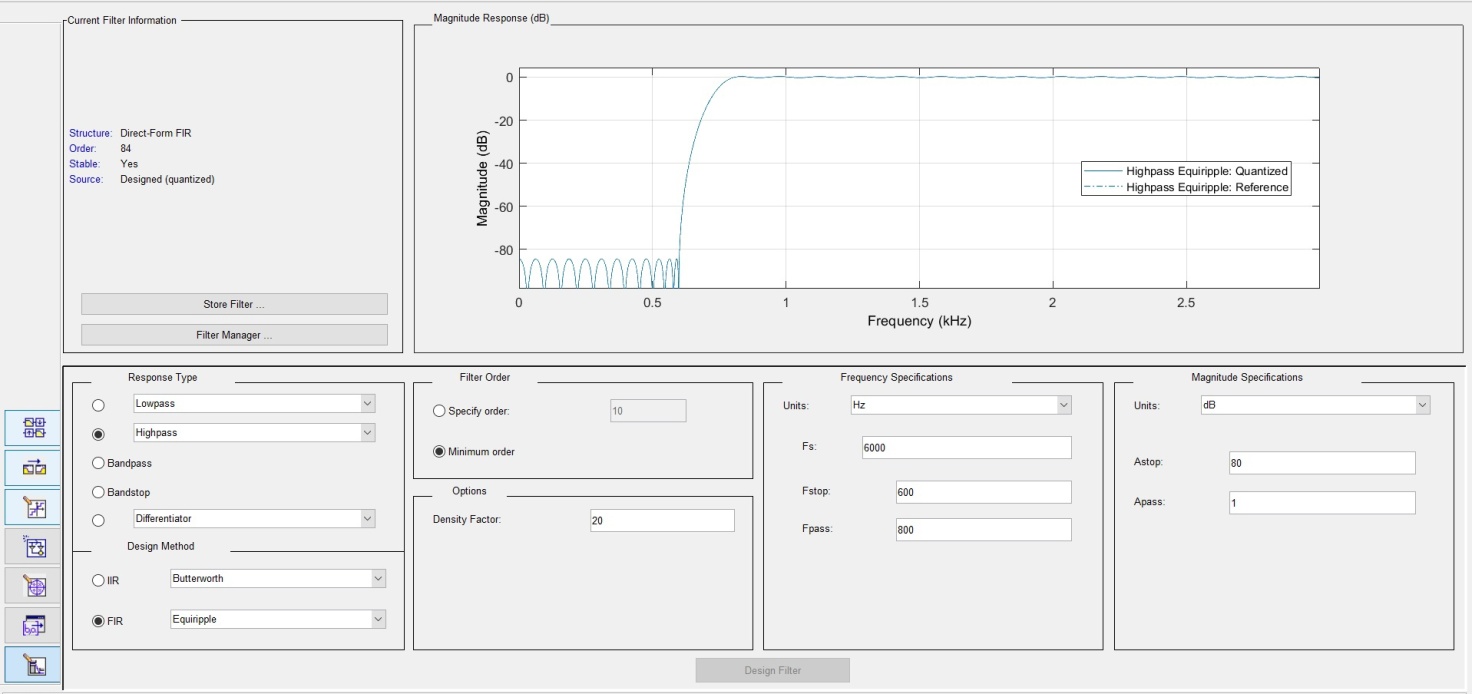
Рисунок 1 - Структура фильтра
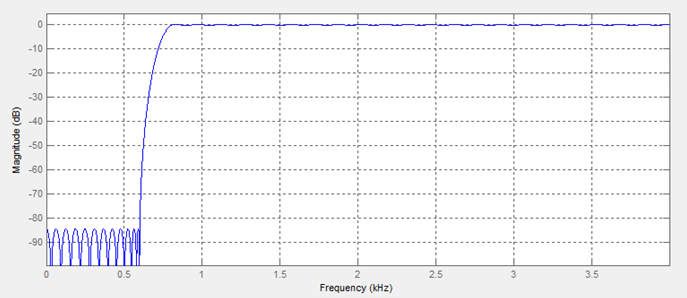
Рисунок 2 – АЧХ фильтра
1.4. АЧХ зоны работы фильтра с целочисленным 8-ми, 16-ти и 32-х разрядным коэффициентами представлены на Рис. 3-5.
При переходе к целочисленным коэффициентам можно сделать следующие выводы:
-
8-ми разрядные коэффициенты фильтра по качеству подавления сигнала абсолютно не подходят для данного фильтра, что связано с ёмкостью переменных; -
Фильтр с 16-ти и 32-х разрядными коэффициентами имеет вполне подходящие характеристики подавления и пропускания.
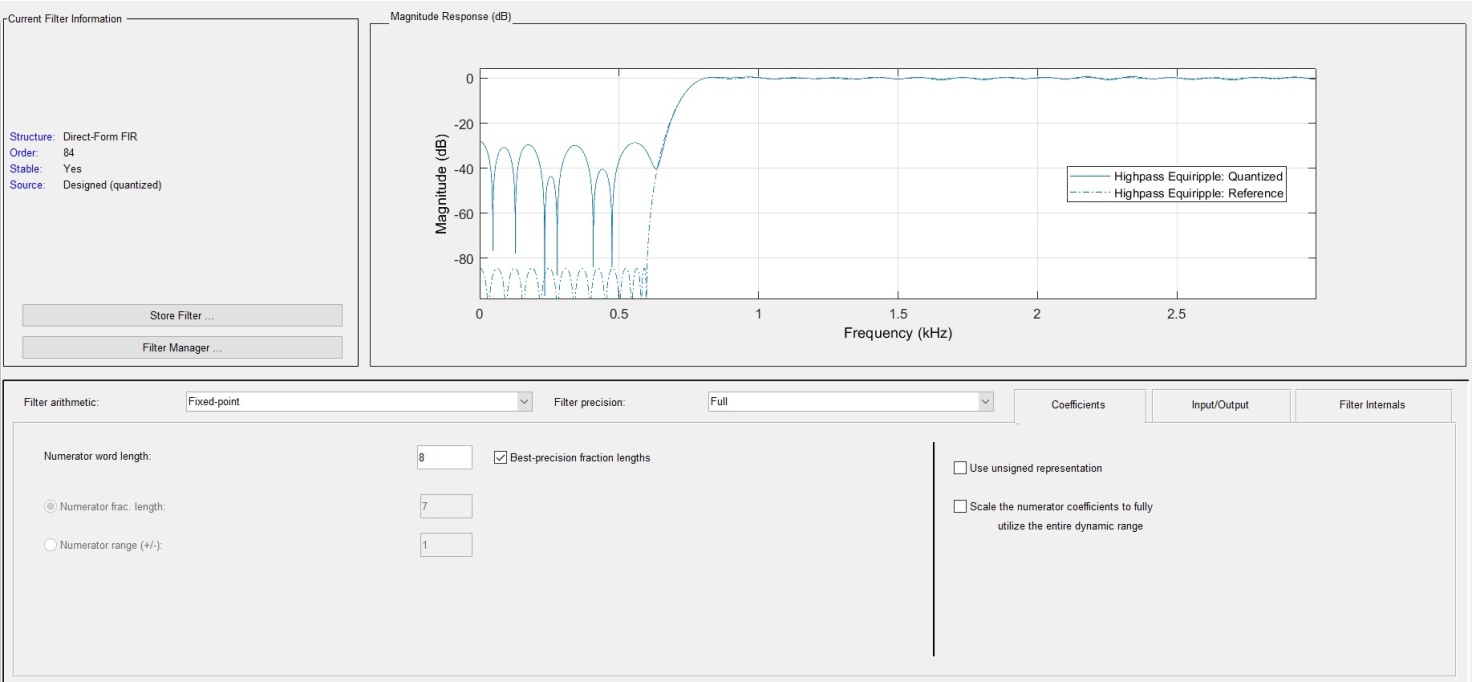
Рисунок 3 – структура и АЧХ фильтра с целочисленным
8-ми разрядным коэффициентами
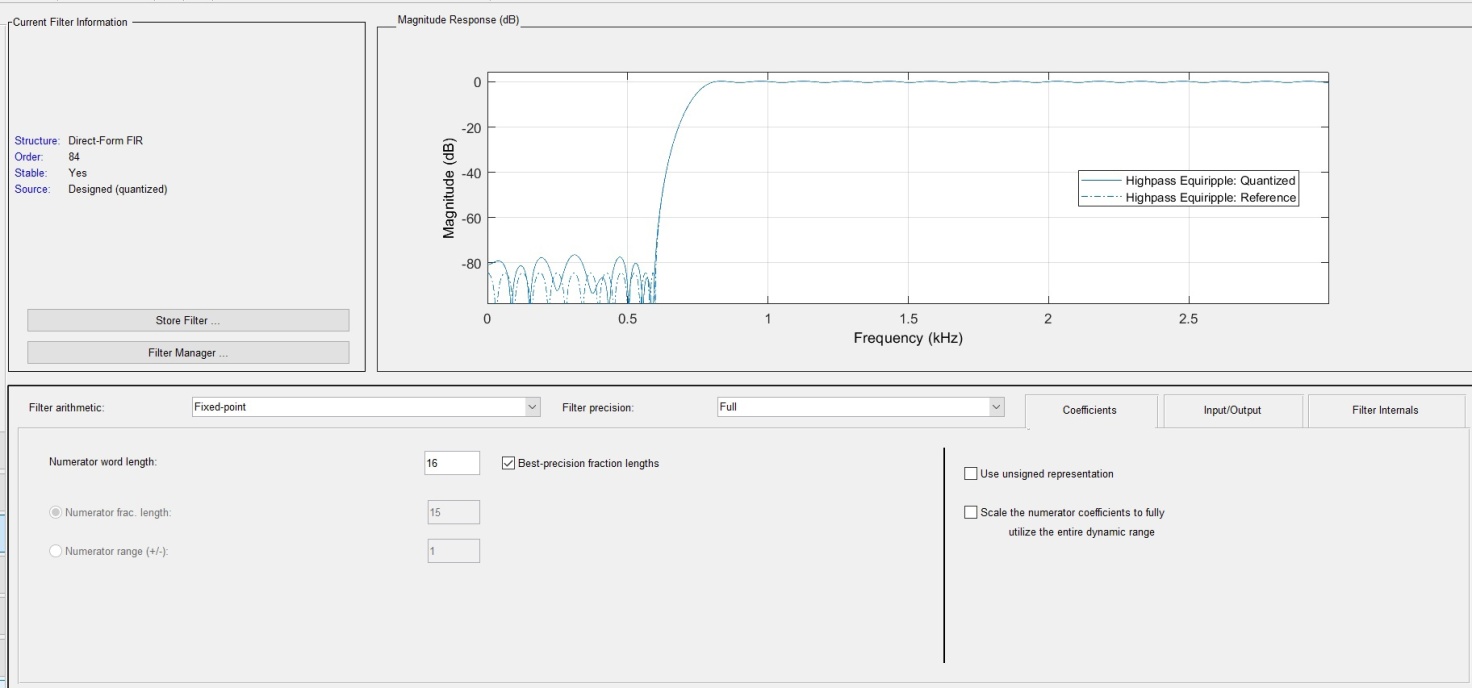
Рисунок 4 – Структура и АЧХ фильтра с целочисленным
16-ти разрядным коэффициентами
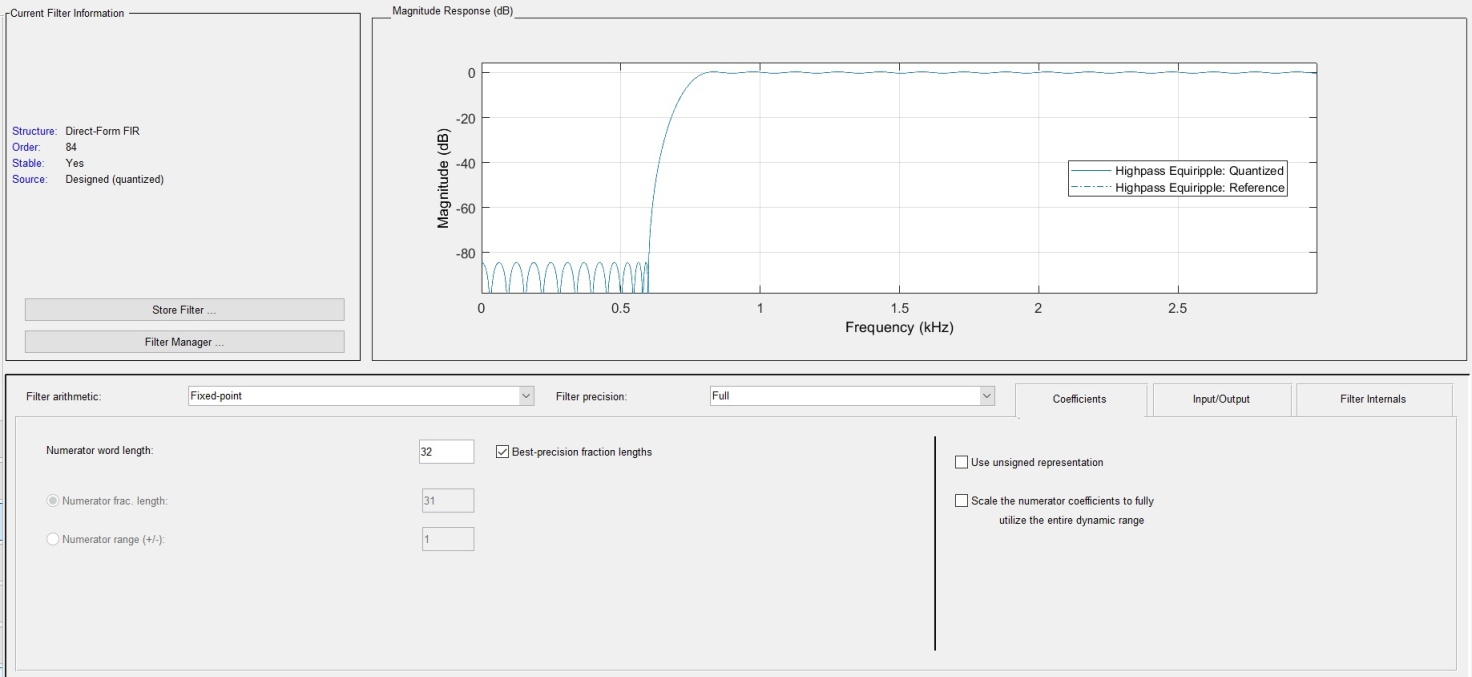
Рисунок 5 – Структура и АЧХ фильтра с целочисленным
32-х разрядным коэффициентами
1.5. Для процедуры интеграции коэффициентов фильтра в среду микроконтроллера необходимо:
-
подключить к лабораторному стенду источник питания и кабель ethernet, генератор сигналов и осциллограф; -
запустить созданный проект, изменить IP-адрес на требуемый, откомпилировать и прошить его в лабораторный стенд; -
результаты работы программы контролировать на осциллографе; -
проверить работу КИХ-фильтра при синусоидальном сигнале во всем диапазоне частот.
1.6. Привести блок-схему программы либо листинг основного кода.
Блок-схема программы представлена на Рис. 6:
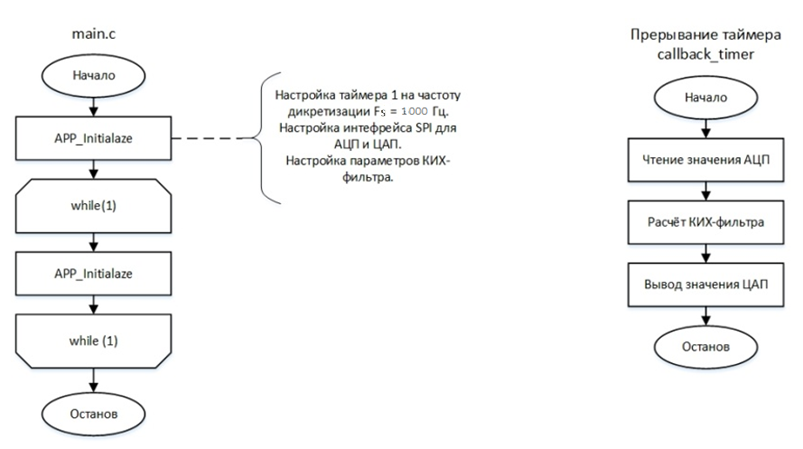
Рисунок 6 – Блок-схема программы
Листинг программы fdacoefs:
#include "tmwtypes.h"
const int BL =112;
const int32_T B[112] = {
9621860, -5842885, -24694070, 16338541, 2578386, 10993081,
650336, -52738, -5718968, -5933171, -6136982, -3023702,
526270, 4641197, 7251358, 7702846, 5375212, 940558,
-4429775, -8858888, -10694379, -8915413, -3715879, 3490780,
10418314, 14520015, 13983617, 8377942, -962270, -11226931,
-18896457, -20894254, -15742372, -4277937, 10356974, 23444107,
30155220, 27161659, 14026754, -6243535, -27724361, -43049757,
-45752917, -32455484, -4598766, 31231171, 64371789, 82517916,
75034682, 35987727, -33541392, -125041340, -223842403, -312209986,
-373327987, 1752342691, -373327987, -312209986, -223842403, -125041340,
-33541392, 35987727, 75034682, 82517916, 64371789, 31231171,
-4598766, -32455484, -45752917, -43049757, -27724361, -6243535,
14026754, 27161659, 30155220, 23444107, 10356974, -4277937,
-15742372, -20894254, -18896457, -11226931, -962270, 8377942,
13983617, 14520015, 10418314, 3490780, -3715879, -8915413,
-10694379, -8858888, -4429775, 940558, 5375212, 7702846,
7251358, 4641197, 526270, -3023702, -6136982, -5933171,
-5718968, -52738, 650336, 10993081, 2578386, 16338541,
-24694070, -5842885, 9621860, 0
};
Задание 2
Для переноса спроектированного фильтра в MATLAB для проведения экспериментов необходимо:
1) В окне Filter Design & Analysis Tool выбрать вкладку Realize Model и нажать кнопку Realize Model.
2) В открывшемся окне Simulink добавить блоки Sine wave, Scope для вывода на конечный график двух сигналов – до и после фильтрации.
3) В окне Model configuration parameters во вкладке Solver выставить следующие параметры:
Type: Fixed-step;
Solver: automatic;
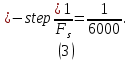
4) Выбрать наиболее подходящее время моделирования. Для варианта 2 это время равно 0.1.
Модель фильтра в матлабе представлена на Рис. 7.
Simulink-модель и графики величины входного и выходного сигналов до регулирования, на границе регулирования и во время регулирования.
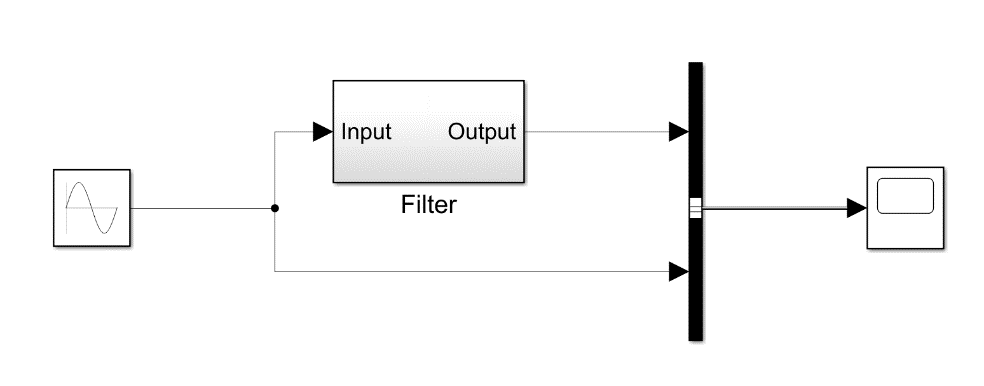
Рисунок 7 – Simulink-модель
На Рис. 8-12 показана работа фильтра при разных частотах. Оранжевый график – исходный сигнал синусоиды с частотой 100 Гц, 500 Гц, 1000 Гц и 5000 Гц соответственно. Фиолетовый график – выходной сигнал фильтра.
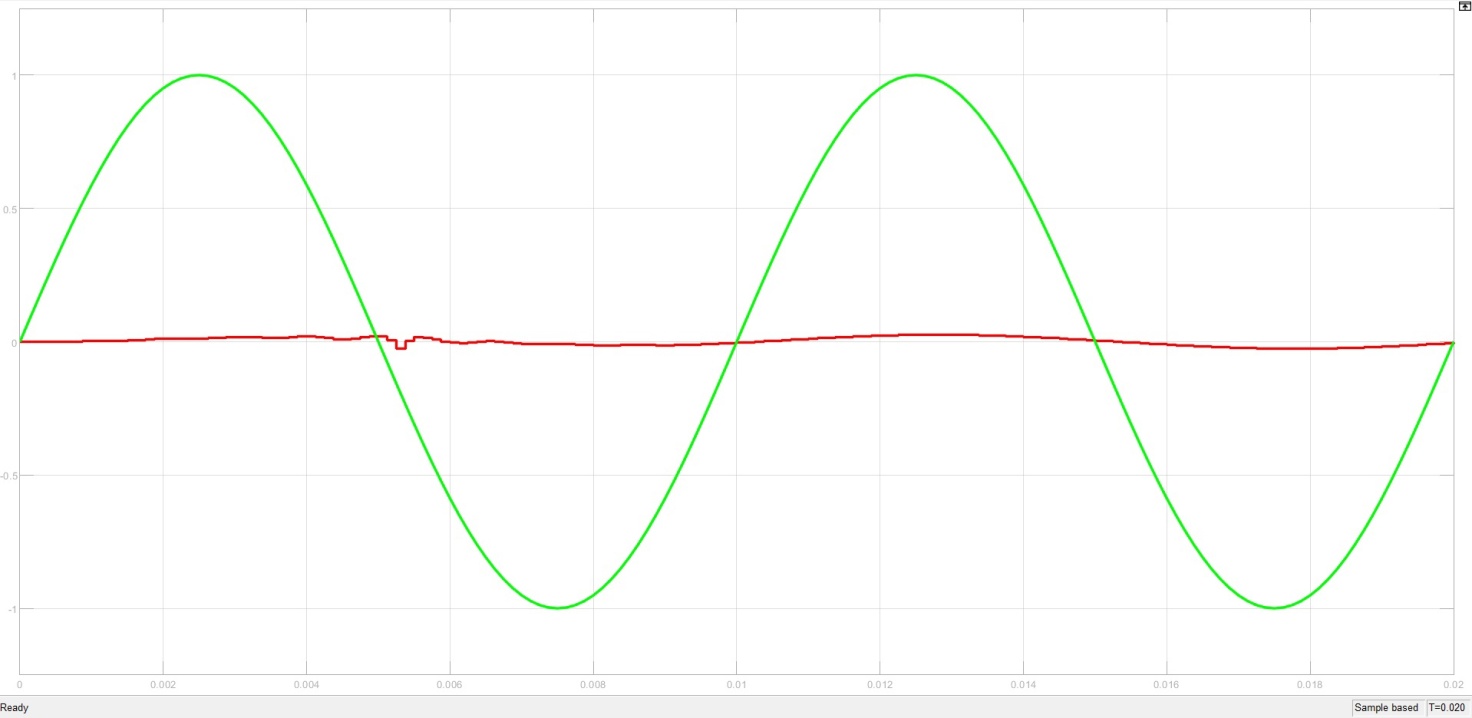
Рисунок 8 – Работа фильтра при частоте 100 Гц и частоте дискретизации 6000Гц
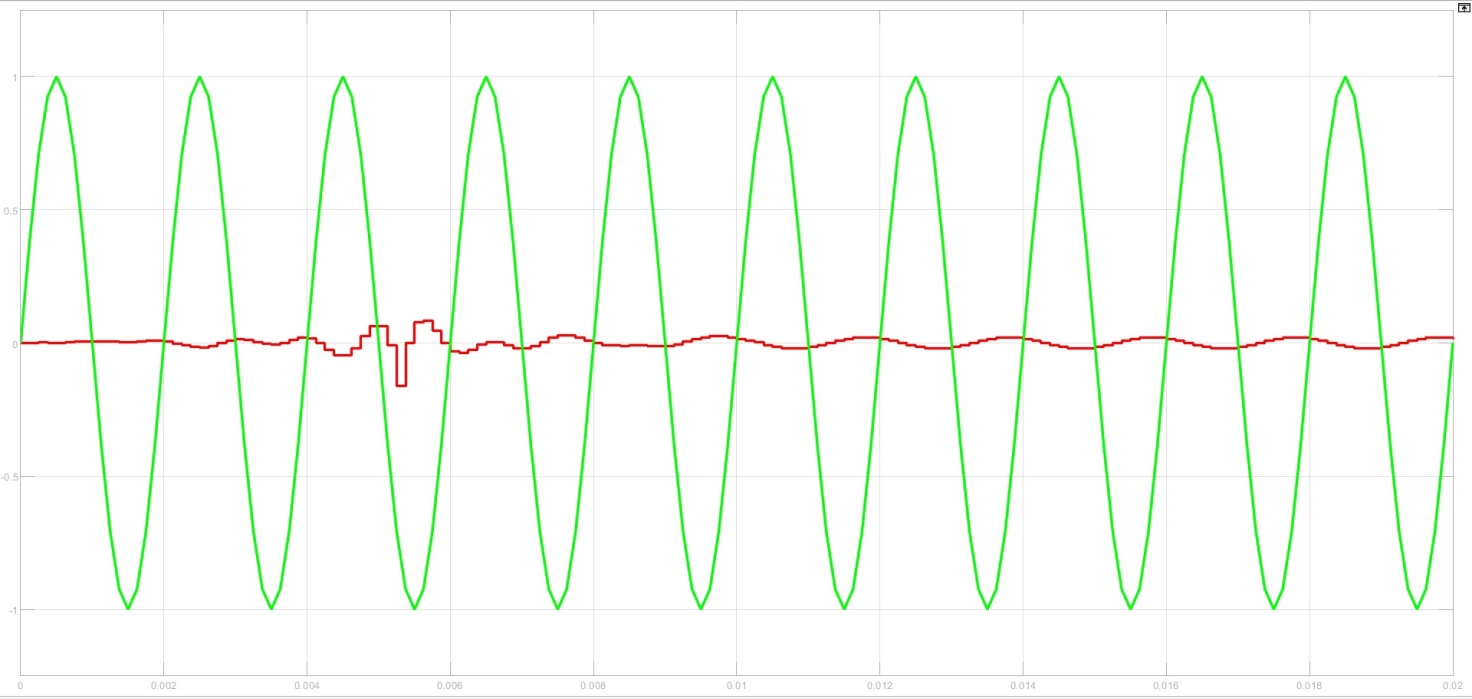
Рисунок 9 – Работа фильтра при частоте 500 Гц и частоте дискретизации 6000 Гц
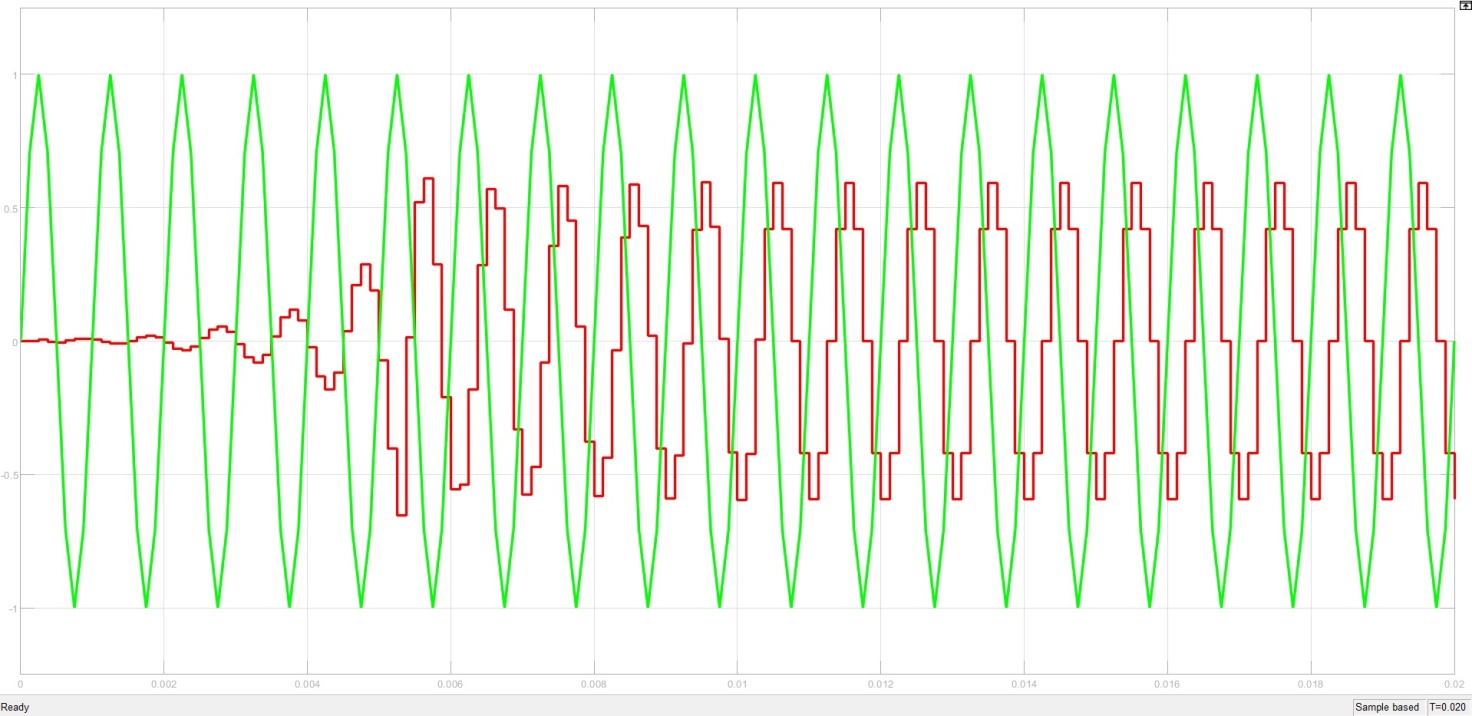
Рисунок 10 – Работа фильтра при частоте 1000 Гц и частоте дискретизации 6000 Гц
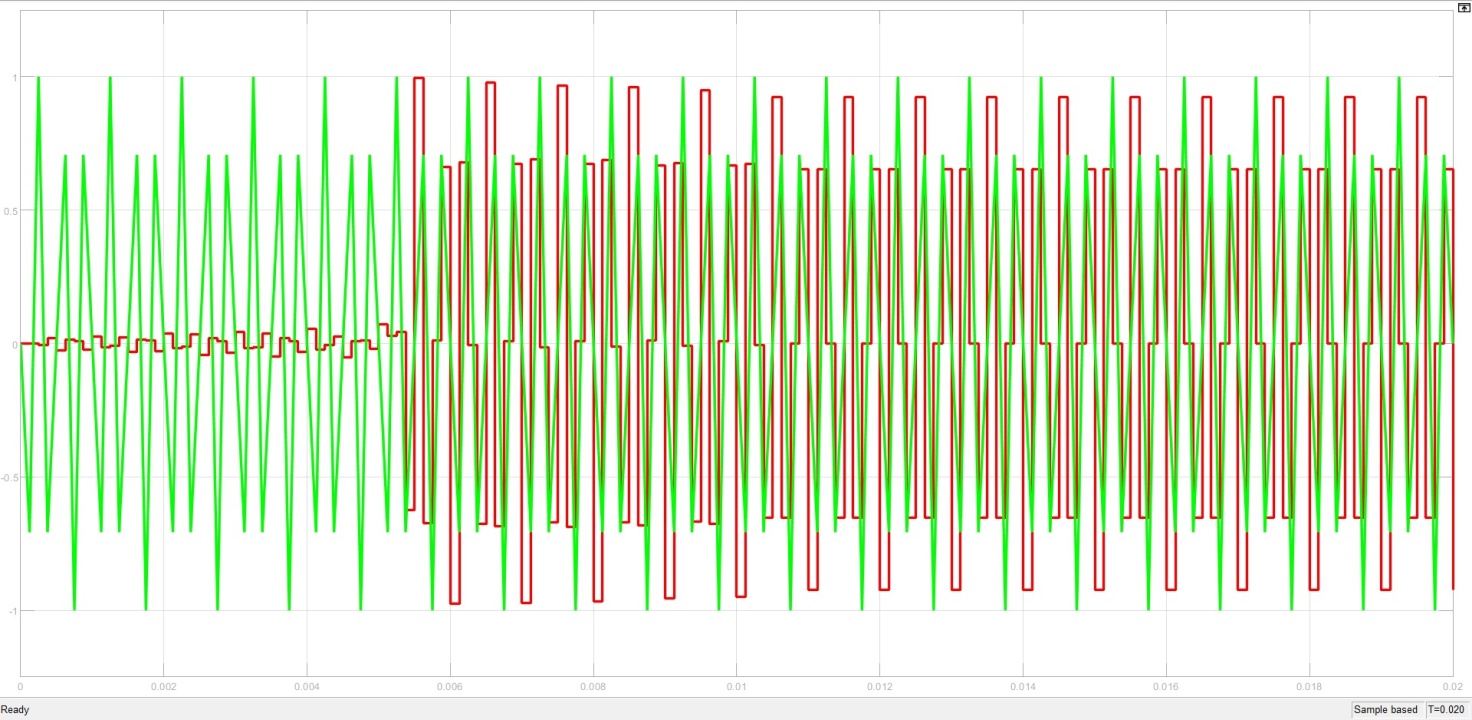
Рисунок 11 – Работа фильтра при частоте 5000 Гц и частоте дискретизации 6000 Гц
Задание 3
3.1 По результатам практических экспериментов были получены данные, представленные в Таблице 2 и на Рис. 12.
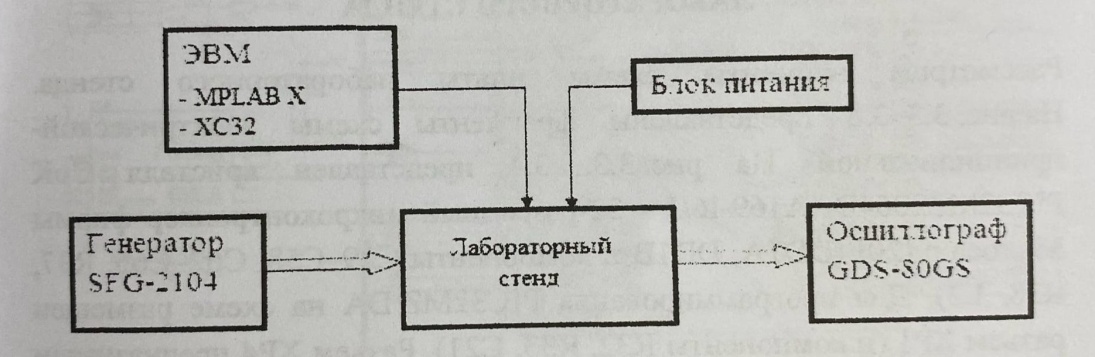
Рисунок 12 – Блок-схема подключения аппаратуры
3.2. Снятие экспериментальной АЧХ реально работающего цифрового фильтра. График экспериментально снятого АЧХ.
Таблица 2
| Частота Гц | Напряжение на выходе |
| 400 | 0,4 V |
| 600 | 0.6 V |
| 650 | 0.8 V |
| 700 | 4.0 V |
| 710 | 4.8 V |
| 750 | 11 V |
| 800 | 18.0 V |
| 900 | 17.8 V |
| 1000 | 19.0 V |
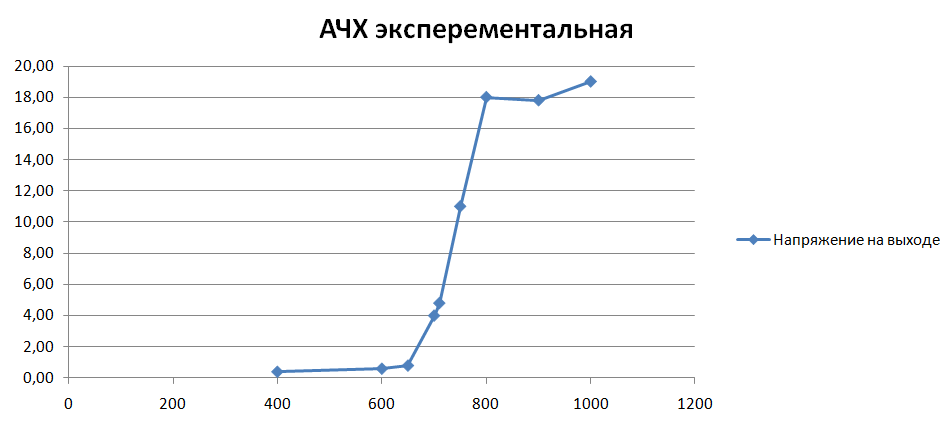
Рисунок 13 - График экспериментальной АЧХ
3.3. Фото собранного лабораторного стенда во время выполнения экспериментов представлено на Рис. 14:
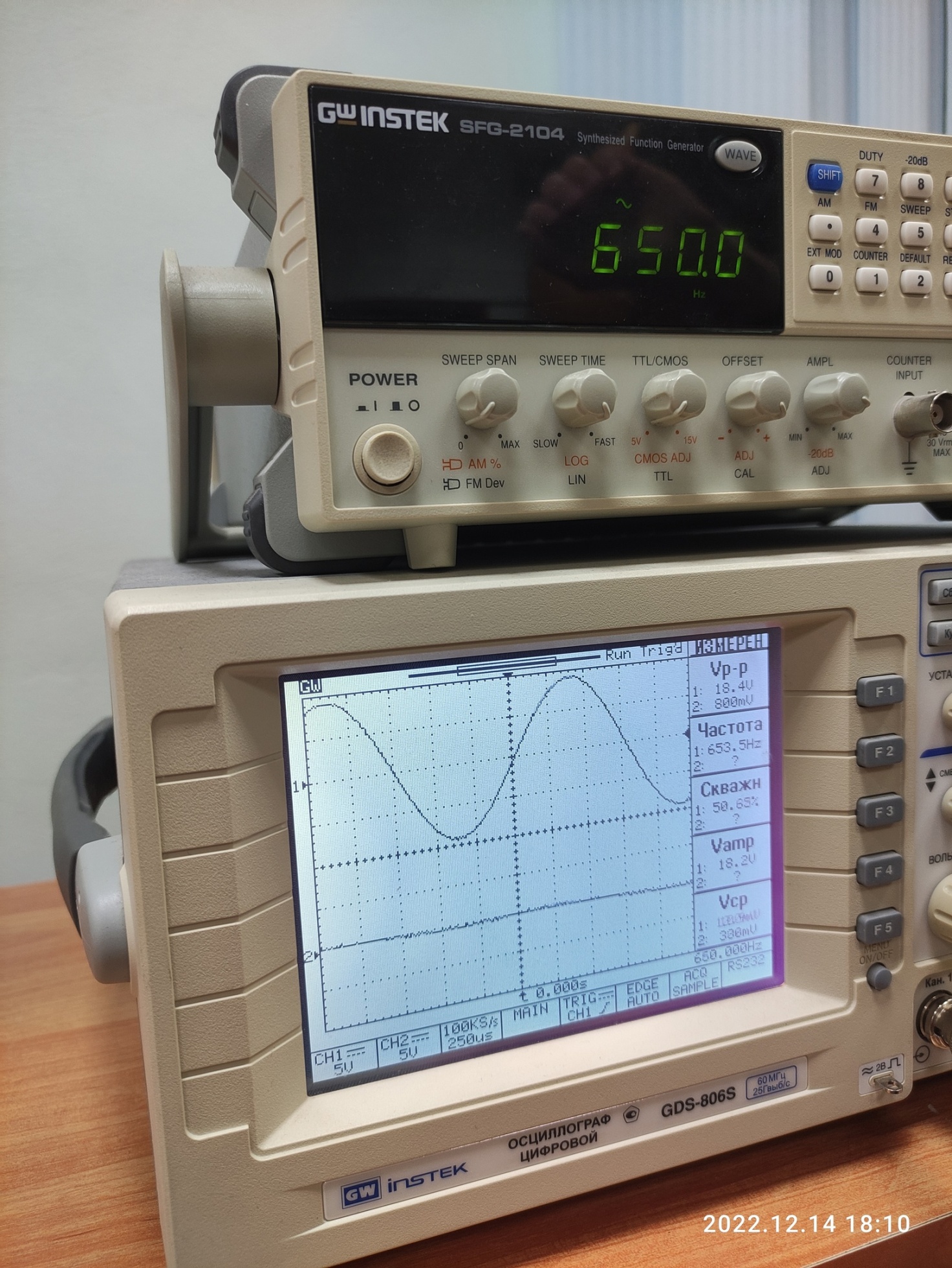
Рисунок 14 – Фото собранного лабораторного стенда
Задание 4
4.1 Частота выходного потока
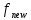 равна:
равна: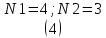
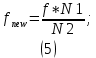
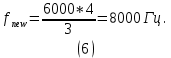
4.2 Блок схема процедуры преобразования частоты дискретизации с применением операций интерполяции и децимации, расчёт и настройка ФНЧ.
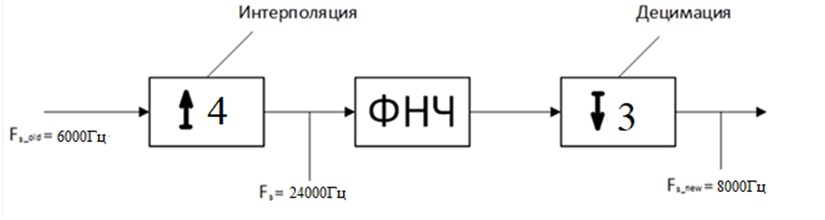
Рисунок 15 – Блок-схема процедуры преобразования частоты дискретизации с применением операций интерполяции и децимации
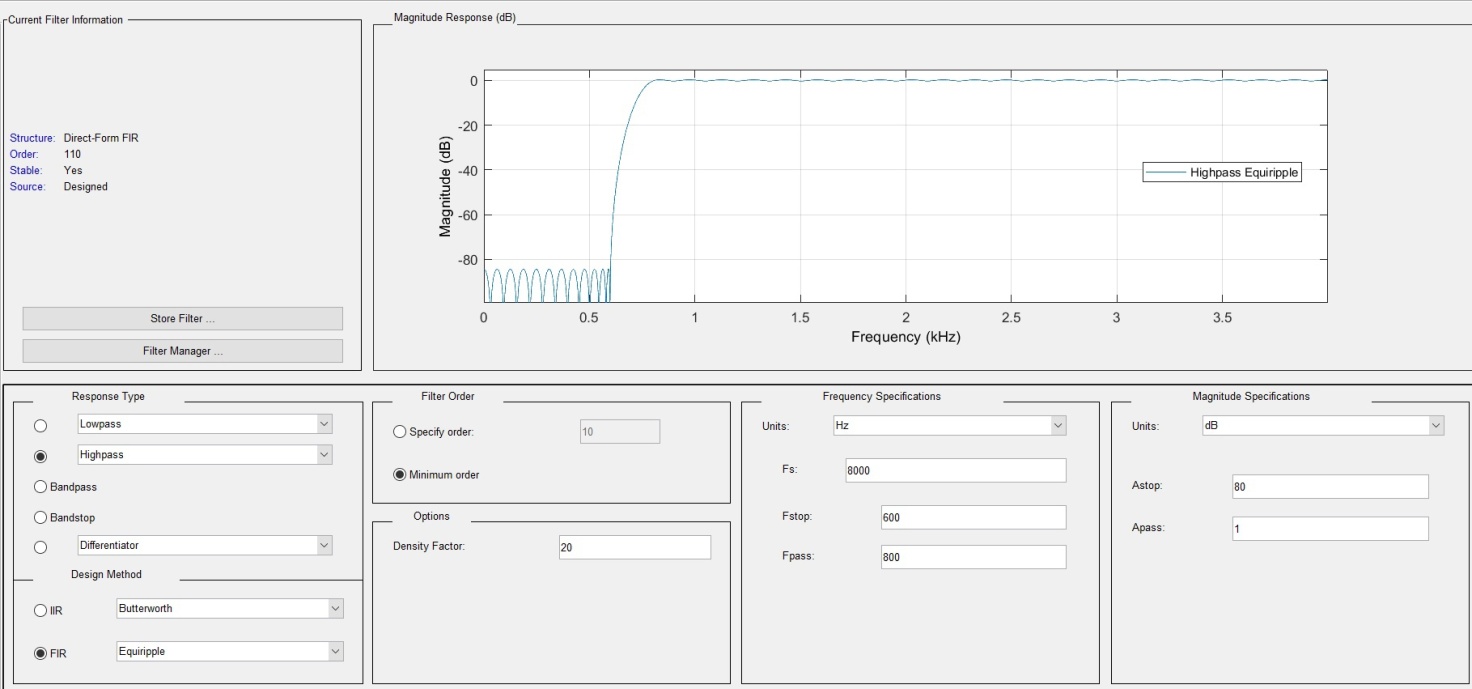
Рисунок 16 – Смоделированный фильтр с частотой дискретизации 8000 Гц
4.3 Интерполяция - повышение частоты дискретизации. При интерполяции необходимо вычислять значения новых отсчетов. Концептуально интерполяция состоит в генерации непрерывной кривой
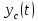 , которая проходит через точки, соответствующие значениям отсчетов
, которая проходит через точки, соответствующие значениям отсчетов 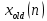 , как показано на Рис. 19(a), с последующей дискретизацией этой кривой с новой частотой дискретизации
, как показано на Рис. 19(a), с последующей дискретизацией этой кривой с новой частотой дискретизации 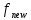 для получения интерполированной последовательности
для получения интерполированной последовательности 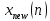 на Рис. 19(b). Непрерывные кривые не могут строиться цифровыми машинами, поэтому необходимо получать
на Рис. 19(b). Непрерывные кривые не могут строиться цифровыми машинами, поэтому необходимо получать 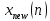 непосредственно из
непосредственно из 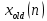 . Для повышения заданной частоты дискретизации в M раз нам необходимо вычислить M-1 промежуточных значений между каждыми двумя соседними отсчетами
. Для повышения заданной частоты дискретизации в M раз нам необходимо вычислить M-1 промежуточных значений между каждыми двумя соседними отсчетами 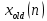 .
.