Файл: Высшая школа электроники и компьютерных наук Кафедра Инфокоммуникационные технологии отчёт по лабораторной работе 1 моделирование передающей части цифровой системы связи.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное
образовательное учреждение высшего образования
«Южно-Уральский государственный университет
(национальный исследовательский университет)»
Высшая школа электроники и компьютерных наук
Кафедра «Инфокоммуникационные технологии»
ОТЧЁТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ № 1
«МОДЕЛИРОВАНИЕ ПЕРЕДАЮЩЕЙ ЧАСТИ ЦИФРОВОЙ СИСТЕМЫ СВЯЗИ»
| | Работу выполнили: Студенты группы КЭ-311 _______________ А.В. Безносова _______________ А.Р. Кзанцева "_____" ________________ 2023 г. |
| | Работу проверил: ______________ В.С. Вдовина "_____" ________________ 2023 г. |
Челябинск 2023
Цель работы: изучение принципов формирования сигнала в системах цифровой связи.
Задачи работы: описание теоретической модели исследуемой системы передачи данных; создание модели передающего устройства цифровой системы связи в Simulink; моделирование работы системы при различных начальных условиях; измерение основных параметров работы передающей системы.
16 КАМ
Квадратурная модуляция - это модуляция, которая основана на суммировании двух сигналов, которые находятся в квадратуре. Другими словами, это модуляция на основе I/Q сигналов.
Термин «I/Q» является аббревиатурой от «in-phase» (синфазный) и «quadrature» (квадратурный), которые относятся к двум синусоидам, что имеют одинаковую частоту и сдвиг по фазе 90°. По соглашению, I-сигнал является сигналом косинусоиды, а Q-сигнал представляет собой сигнал синусоиды. Как вы знаете, волна синусоиды (без какой-либо дополнительной фазы) сдвинута относительно волны косинусоиды на 90°. Другой способ выразить это состоит в том, что сигналы синусоиды и косинусоиды являются квадратурными сигналами. Эти сигналы I/Q всегда модулируются по амплитуде, а не по частоте или фазе.
16 – позиционная квадратурная амплитудная модуляция - модуляция
, при которой промодулированный сигнал представляет собой сумму двух ортогональных несущих: косинусоидальной и синусоидальной, амплитуды которых принимают независимые дискретные (-3, -1,1,3). Эти дискретные значения являются четырьмя сигнальными значения для каждой из квадратурных компонент I и Q. Этим достигаются 16 значений суммарного сигнала, т.е.
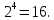
В конкретный момент времени каждая несущая несет информацию 4 бита. Соседние по горизонтали и вертикали символы отличаются только в одном бите. Следовательно, если при демодуляции происходит ошибка из-за помех и за демодулированный символ принимается соседний (а такие ошибки наиболее вероятны), то это приводит к ошибке только в одном бите.
Модель
В данной работе нам необходимо создать модель для 16-позиционной квадратурой амплитудной модуляцией (КАМ). Для этого нам необходимо в библиотеках Simulink найти все ниже перечисленные элементы:
-
Random Integer Generator – генератор случайных целых чисел; -
1-D Lookup Table – таблица соответствий (истинности); -
Raised Cosine Transmit Filter – формирующий фильтр с характеристикой корень из приподнятого косинуса; -
Gain – усилитель сигнала; -
Complex to Real-Imag – блок выделения реальной и мнимой части комплексного сигнала; -
Scope – осциллограф; -
Eye Diagram – блок отображения глазковой диаграммы сигнала; -
Constellation Diagram – блок отображения диаграммы рассеяния сигнала; при помощи него же мы можем произвести отображения траектории вектора комплексной огибающей сигнала на плоскости, включив в блоке функцию «Signal Trajectory»; -
Subsystem – подсистема, позволяет оформить часть модели в виде отдельного блока; -
Spectrum Analyzer – анализатор спектра сигнала.
Сначала нам необходимо собраться Modulator – подсистема формирователя сигнала цифрового передатчика.
В него входят 1-D Lookup Table, Raised Cosine Transmit Filter, Gain, два блока Eye Diagram и четыре блока Constellation Diagram из них два блока, отображающих траекторию вектора комплексной огибающей сигнала на плоскости, т.е. Signal Trajectory, и два блока, отображающих диаграммы рассеивания. Соберем эти элементы в схему в показанную на рисунке (1).
В 1-D Lookup Table содержатся комбинации сигнальных значений, на основе которых будет проходить модуляция
, Eye Diagram, Constellation Diagram, Constellation Diagram3 показывающие соответствующие диаграммы исходной 16-КАМ, затем мы пропускаем сигналы через формирующий фильтр Raised Cosine Transmit Filter и подадим через Eye Diagram1, Constellation Diagram1, Constellation Diagram2, которые уже снимает показания после преобразования.
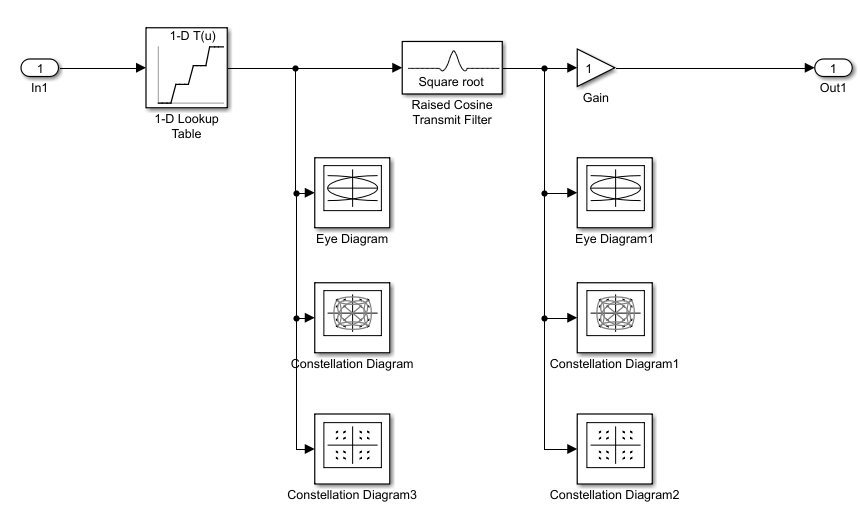
Рисунок 1 – Схема Модулятора.
После того как мы собрали схему, свернём её в Subsystem, и приступаем к сбору общего вида модели передающего устройства. Для этого нам необходимы Random Integer Generator, Spectrum Analyzer, Scope, Complex to Real-Imag. Подключим Random Integer Generator к Subsystem, которая выступает в роле модулятора, затем к ней подключим Spectrum Analyzer, Scope, Complex to Real-Imag, как показано на рисунке 2.
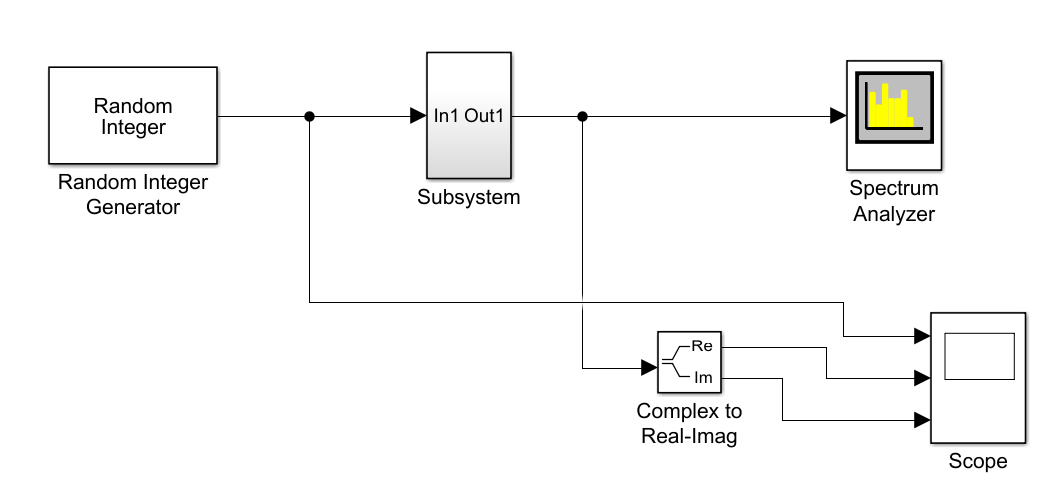
Рисунок 2 – Общий вид модели.
Д
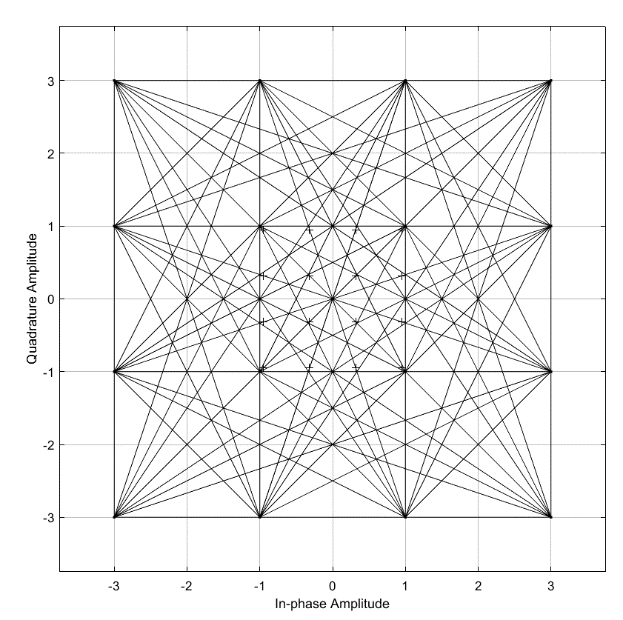
алее перейдём к выполнению задания, в котором нам необходимо перестраивать формирующий фильтр путём изменения коэффициент скругления и наблюдать за возникновением изменением в диаграммах. Отметим, что показания Eye Diagram, Constellation Diagram, Constellation Diagram3 не будут менять в ходе перенастроек, поскольку они подключены до фильтра и отображают состояния исходных сигналов. Из-за чего мы приведём их показания отдельно, чтобы в дальнейшем не повторять их при каждом коэффициенте скругления.
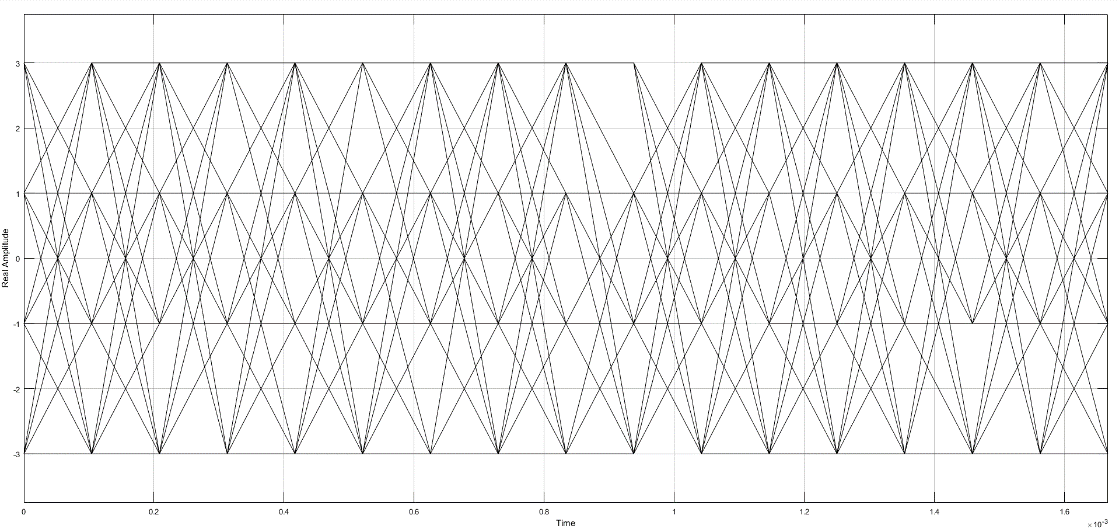
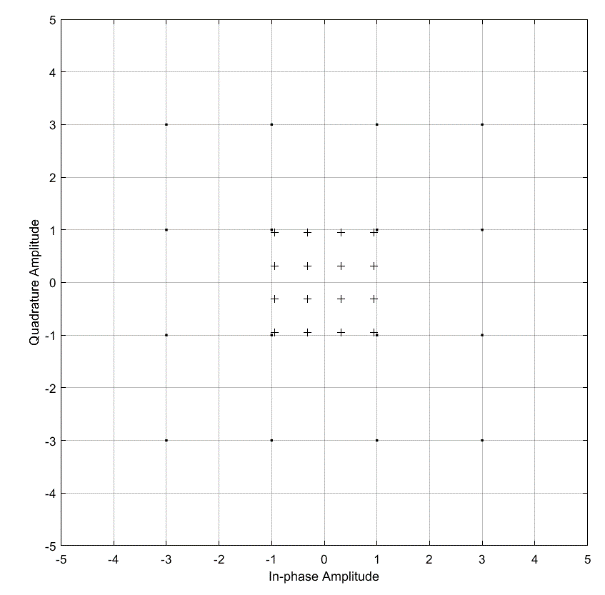
Рисунок 3 – Сигнальное созвездие. Рисунок 4 – Траектория сигнала.
Рисунок 5 - Глазковая диаграмма исходной модуляции.
Далее мы установим коэффициент скругления на 0 и посмотрим на диаграммы.
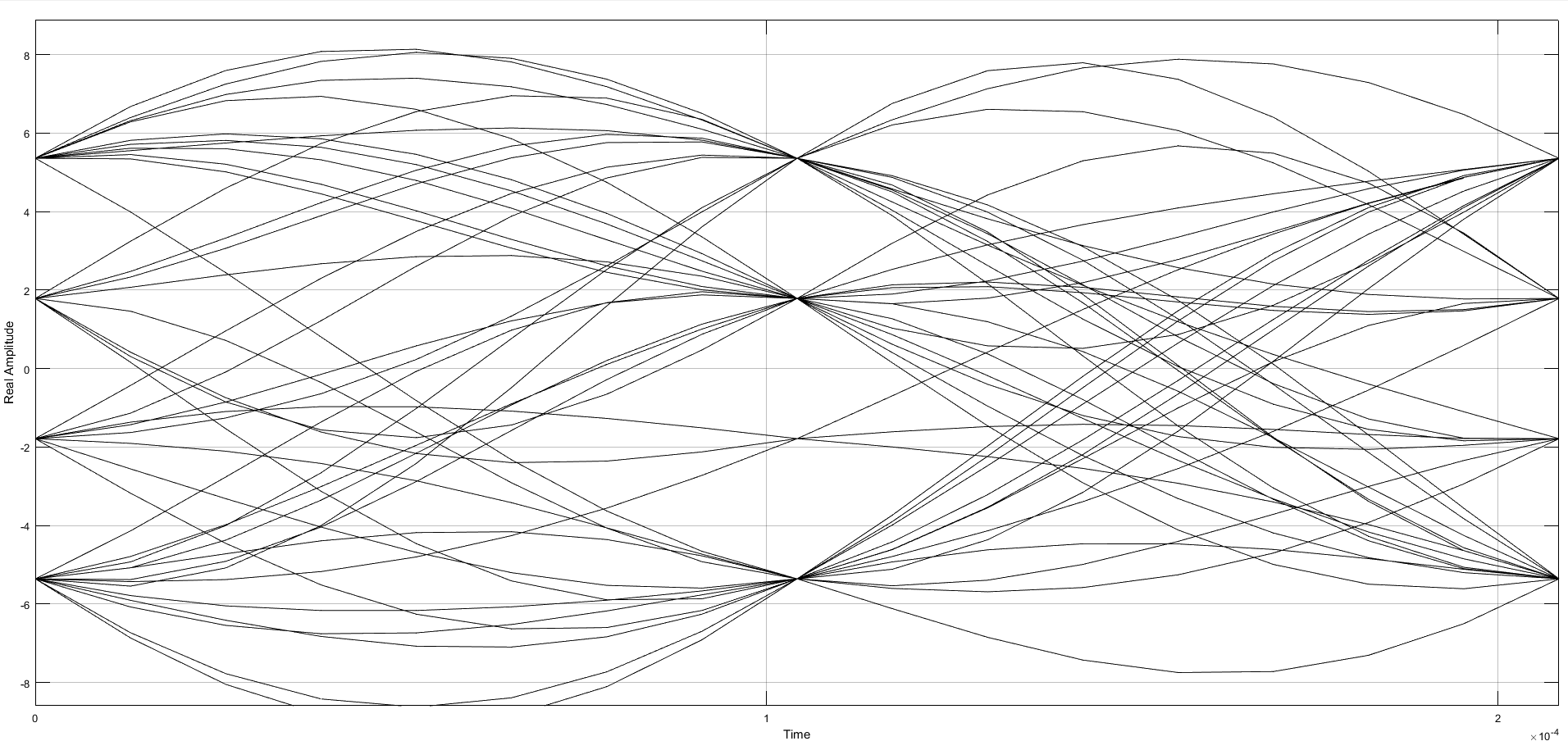
Рисунок 6 – Глазковая диаграмма при коэффициенте 0
Р
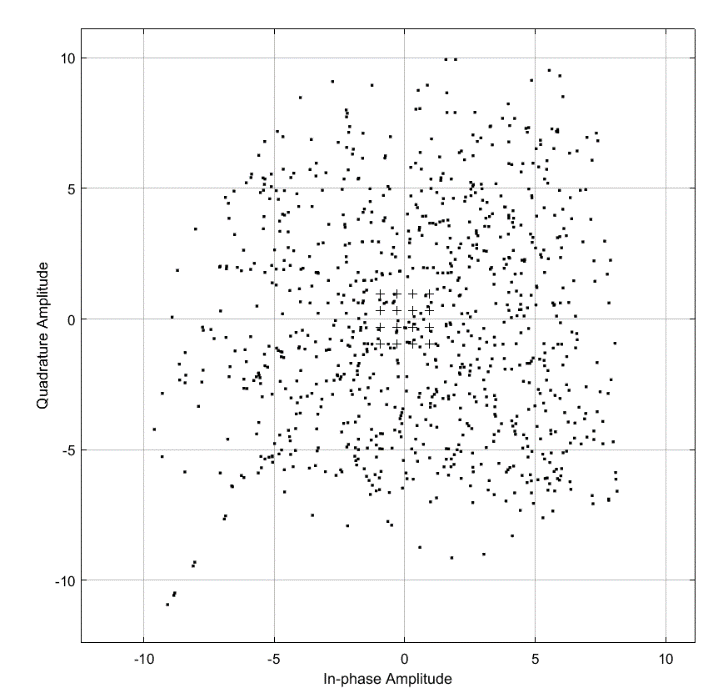
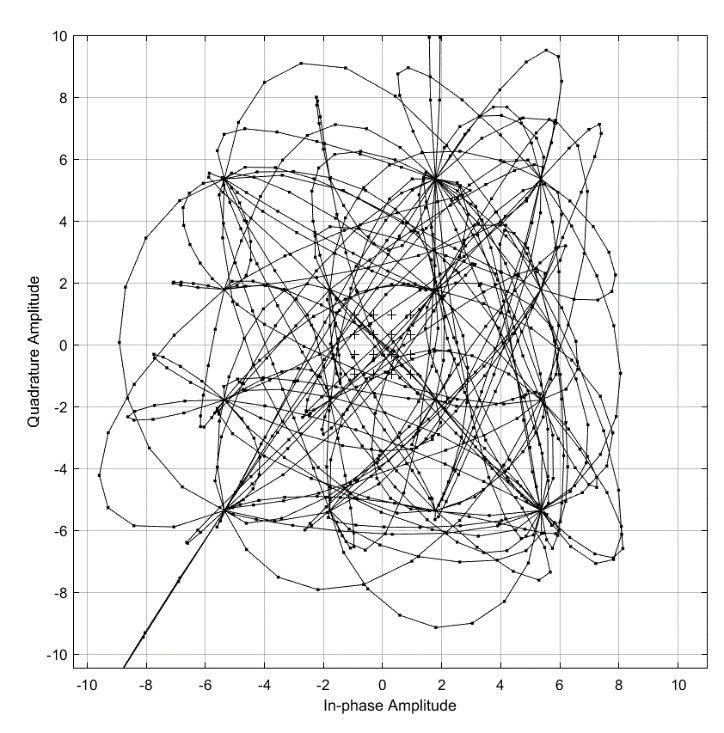
исунок 6 – Сигнальное возведение. Рисунок 7 – Траектория сигнала.
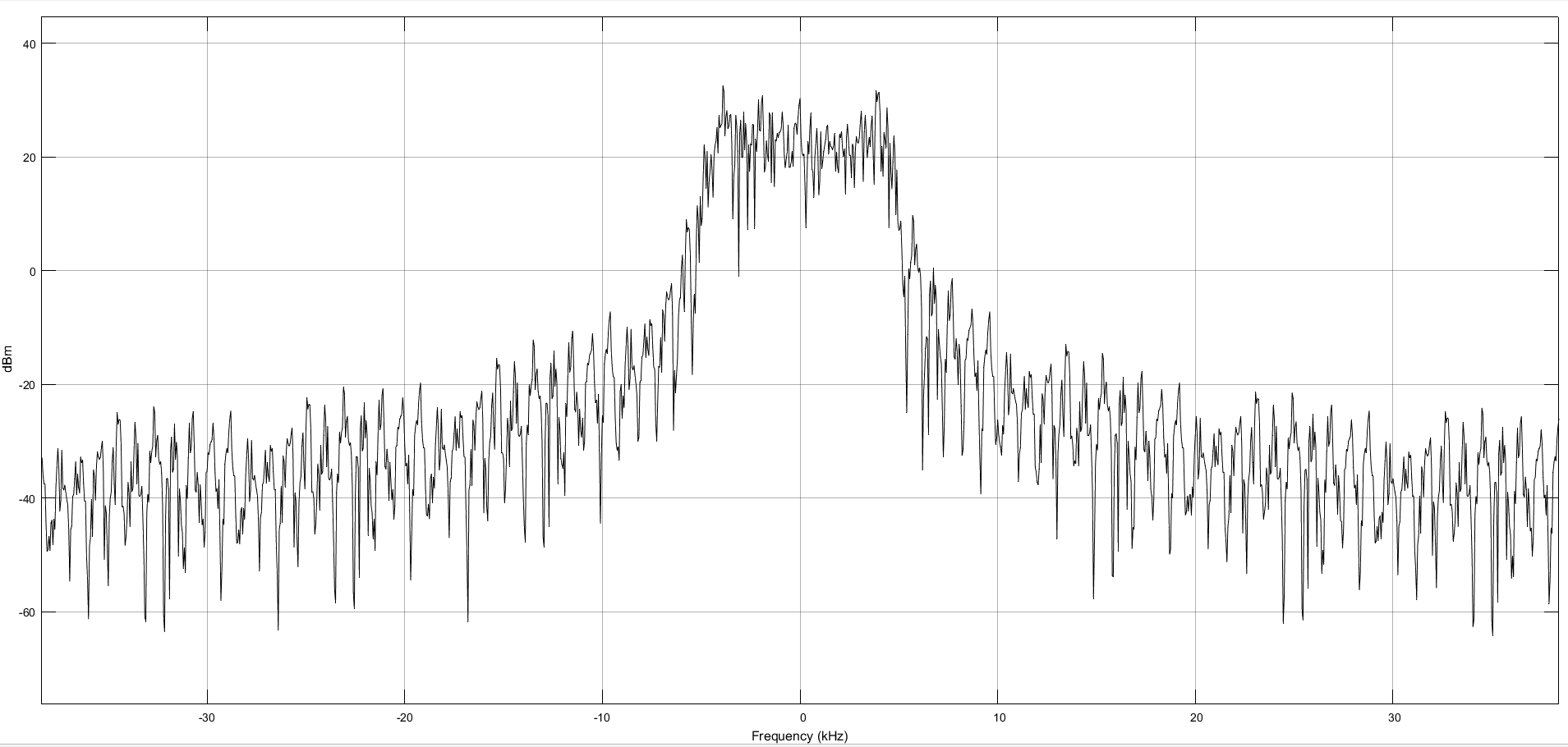
Рисунок 9 – Спектр формируемого сигнала.
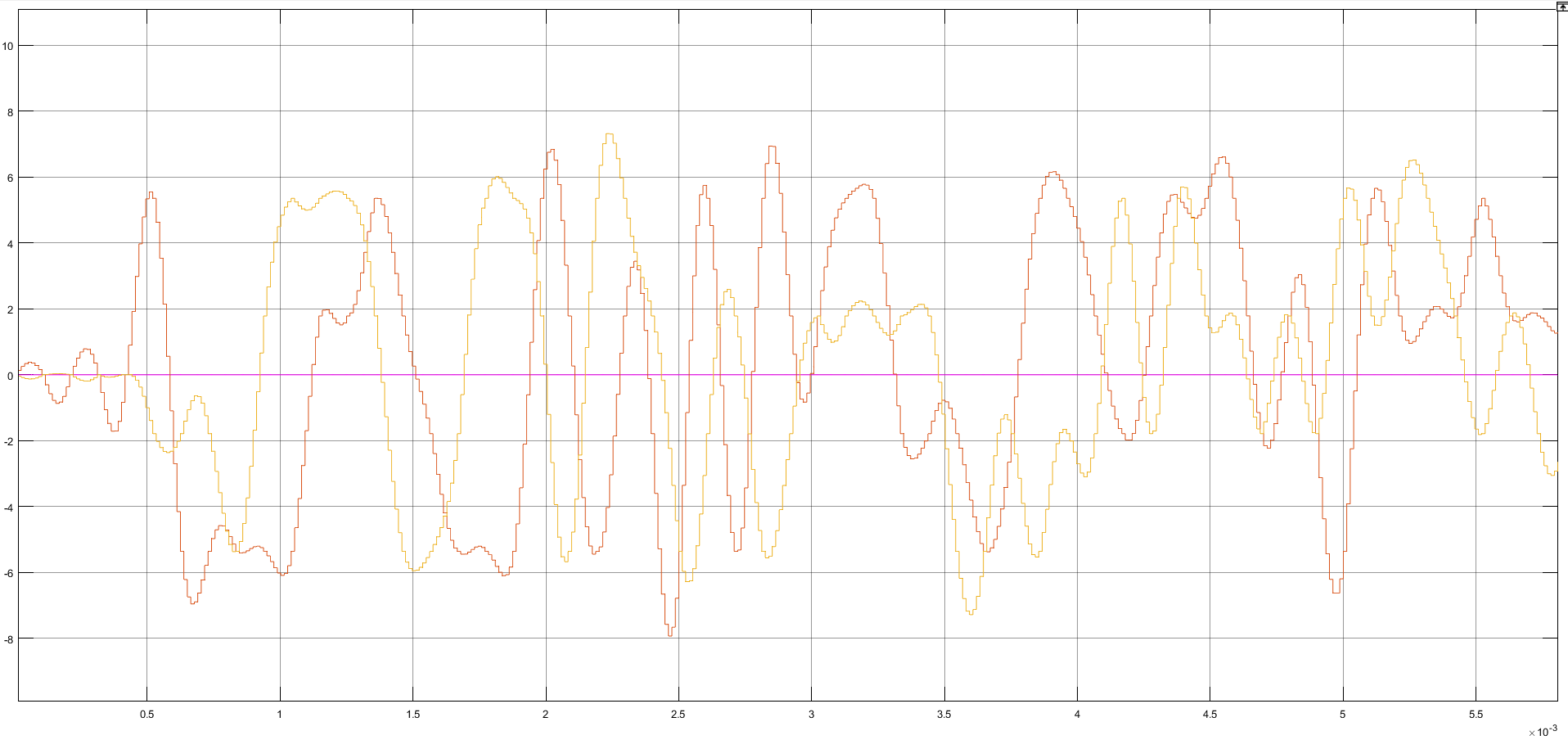
Рисунок 10 – Осциллограммы шины данных и комплексной огибающей сформированного сигнала.
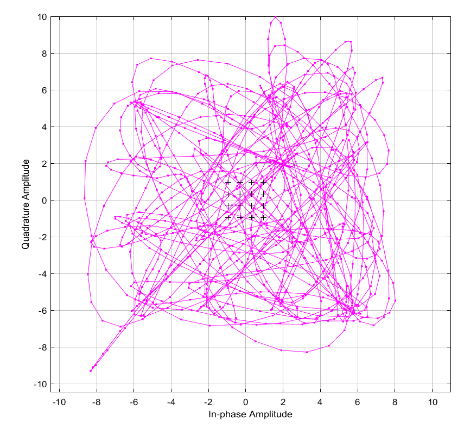
Рисунок 12 – Траектория.
Рисунок 11 – Сигнальное созвездие.
П
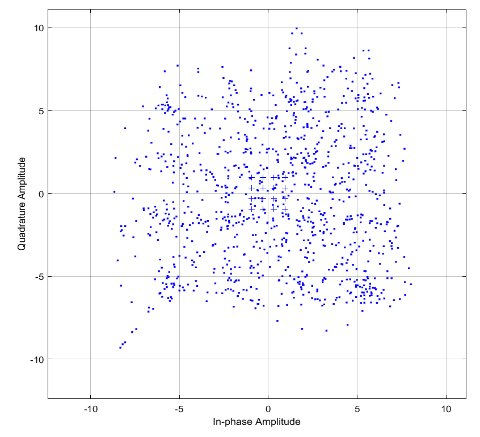
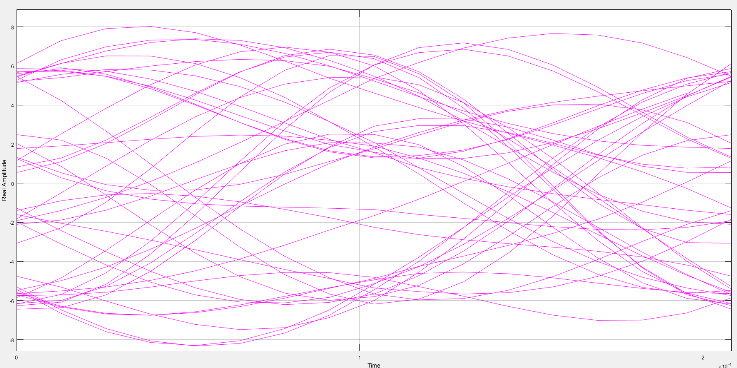
ри коэффициенте скругления 0.2.
Рисунок 13 – Глазковая диаграмма.
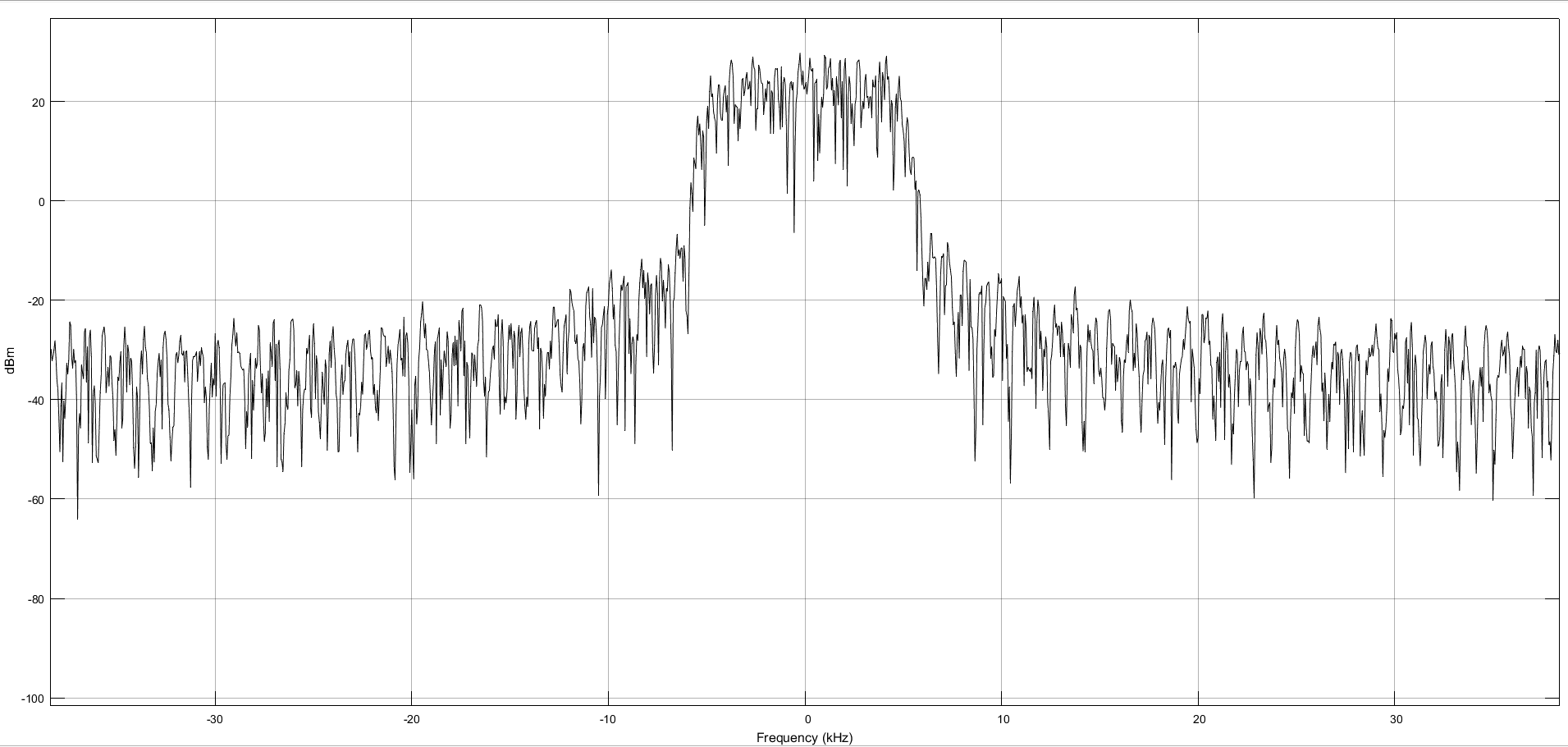
Рисунок 14 – Спектр формируемого сигнала.
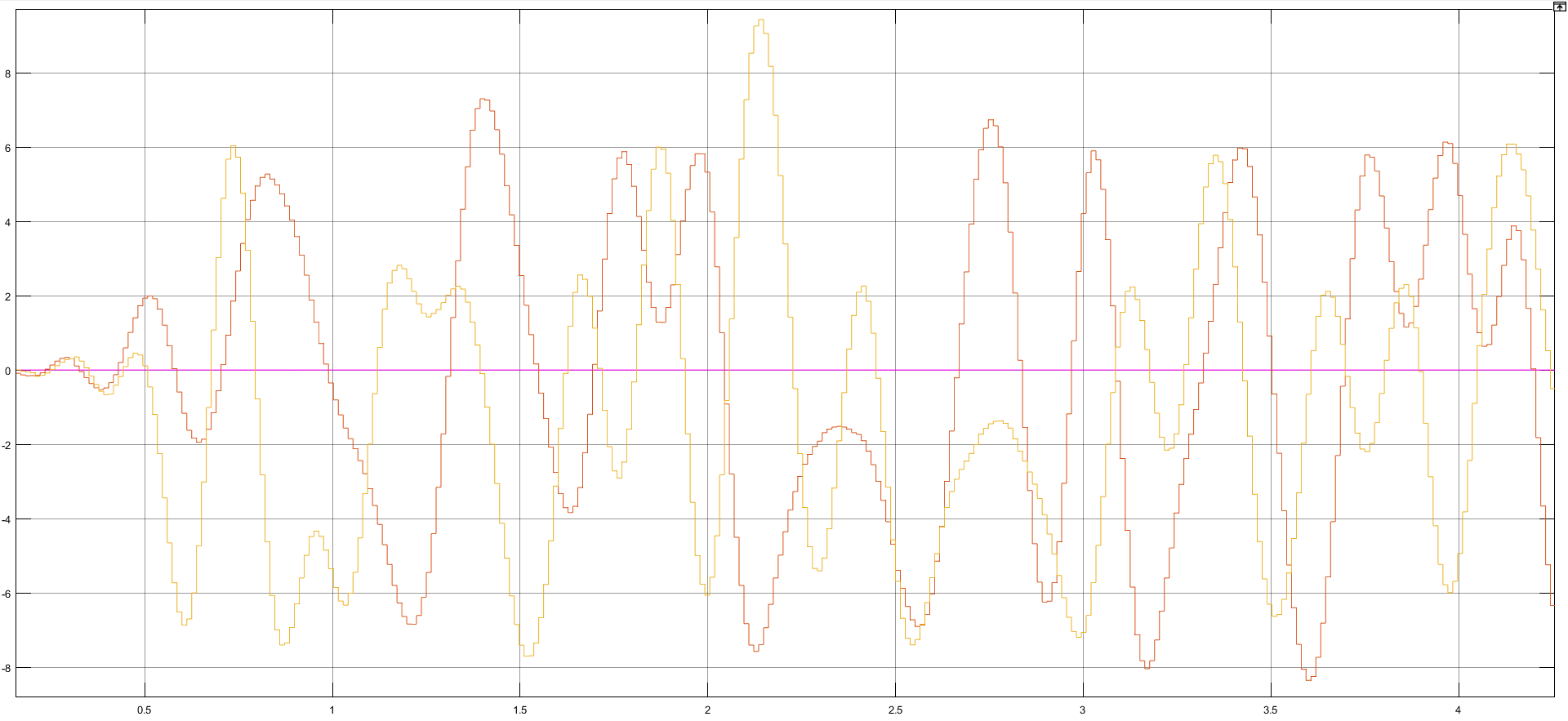
Рисунок 15 – Осциллограммы комплексных амплитуд.
П
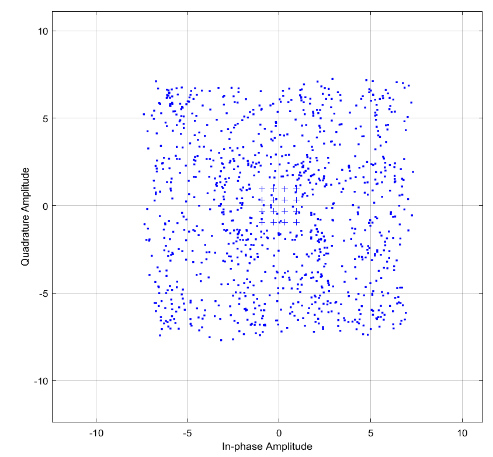
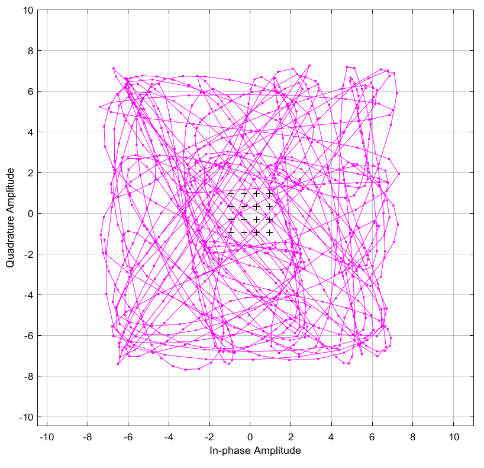
ри коэффициенте скругления 0.4.
Р
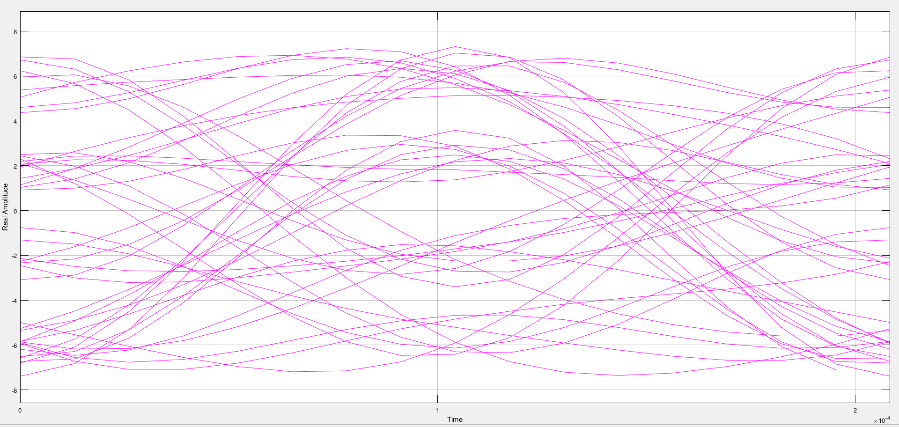
исунок 16 - Траектория Рисунок 17 – Созвездие.
Рисунок 18 – Глазковая диаграмма.
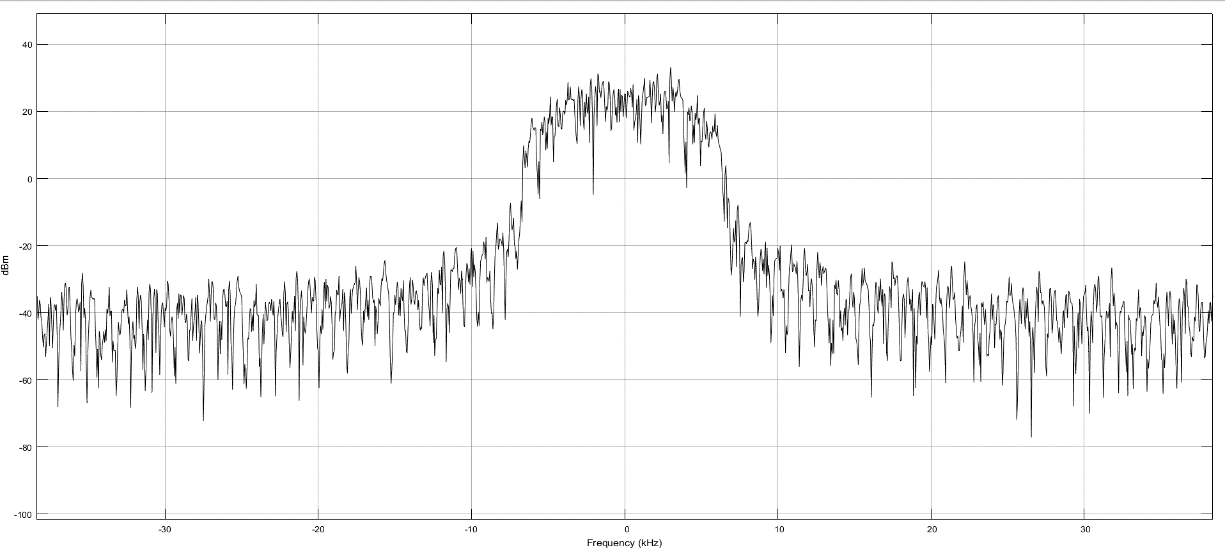
Р
исунок 19 – Спектр при коэффициенте 0.4.
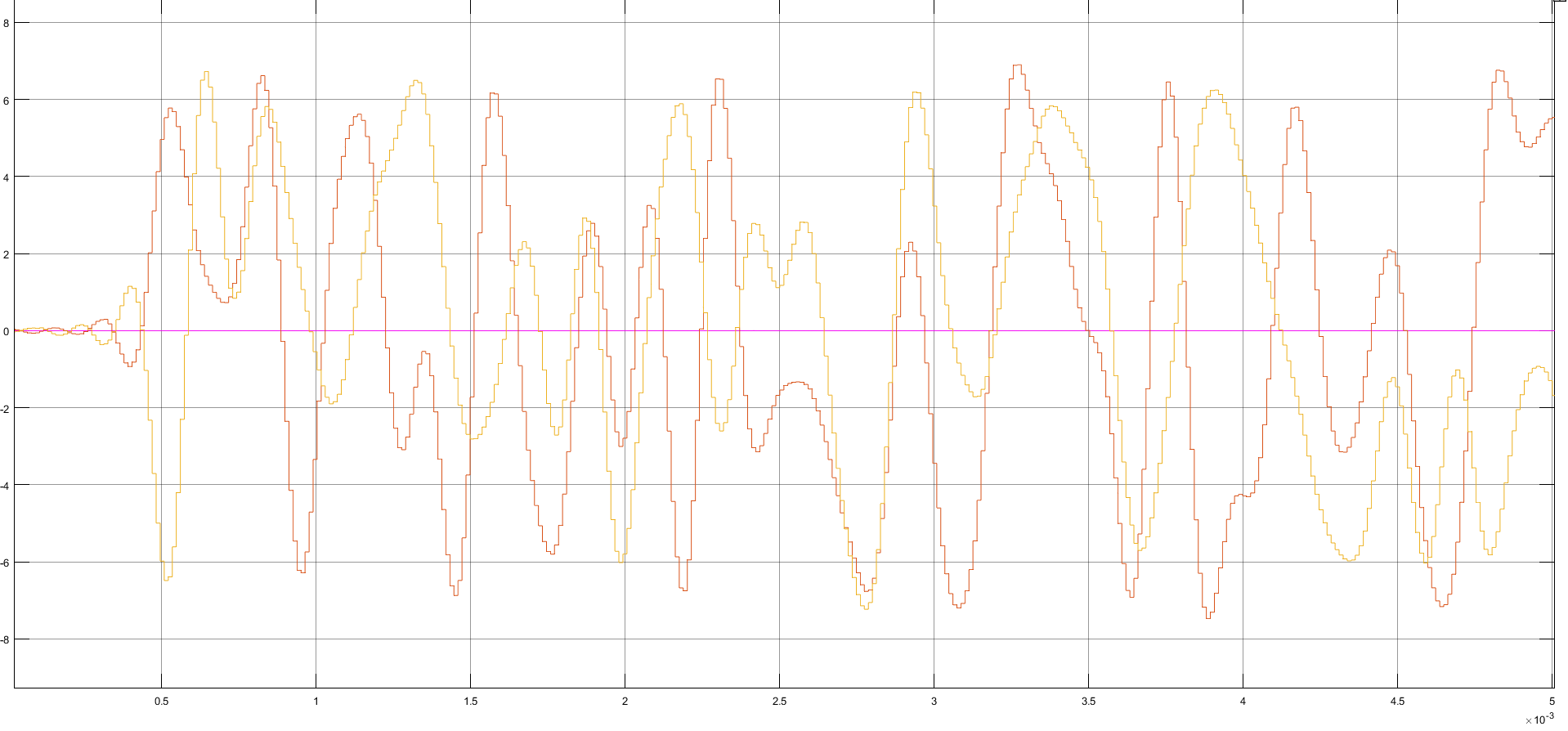
Рисунок 20 – Осциллограммы амплитуд.
При коэффициенте сглаживания 0.6.
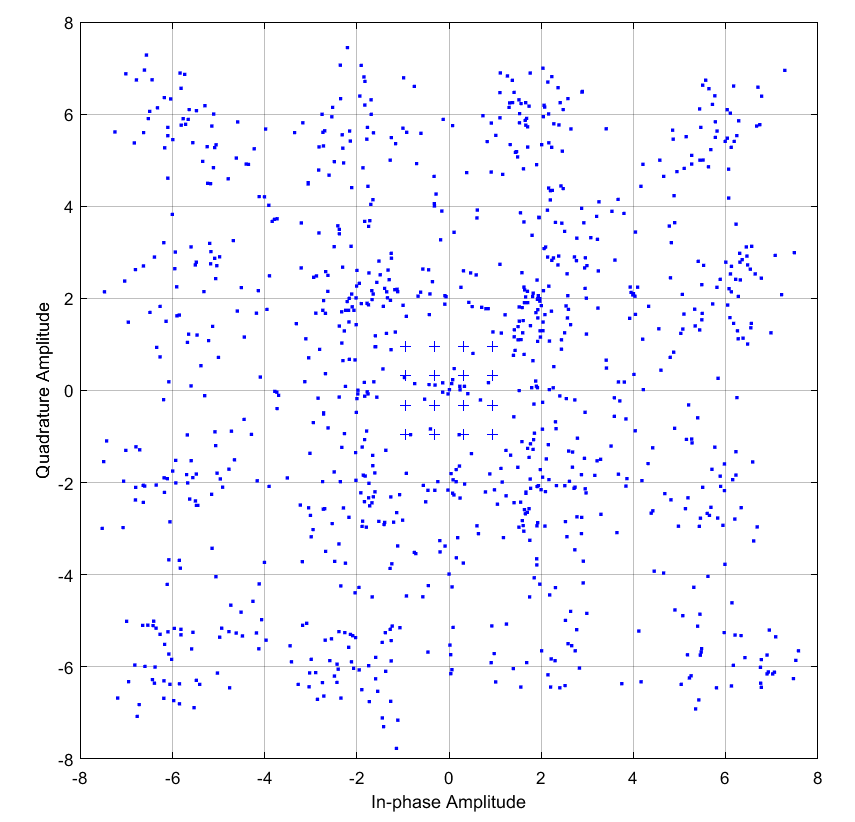
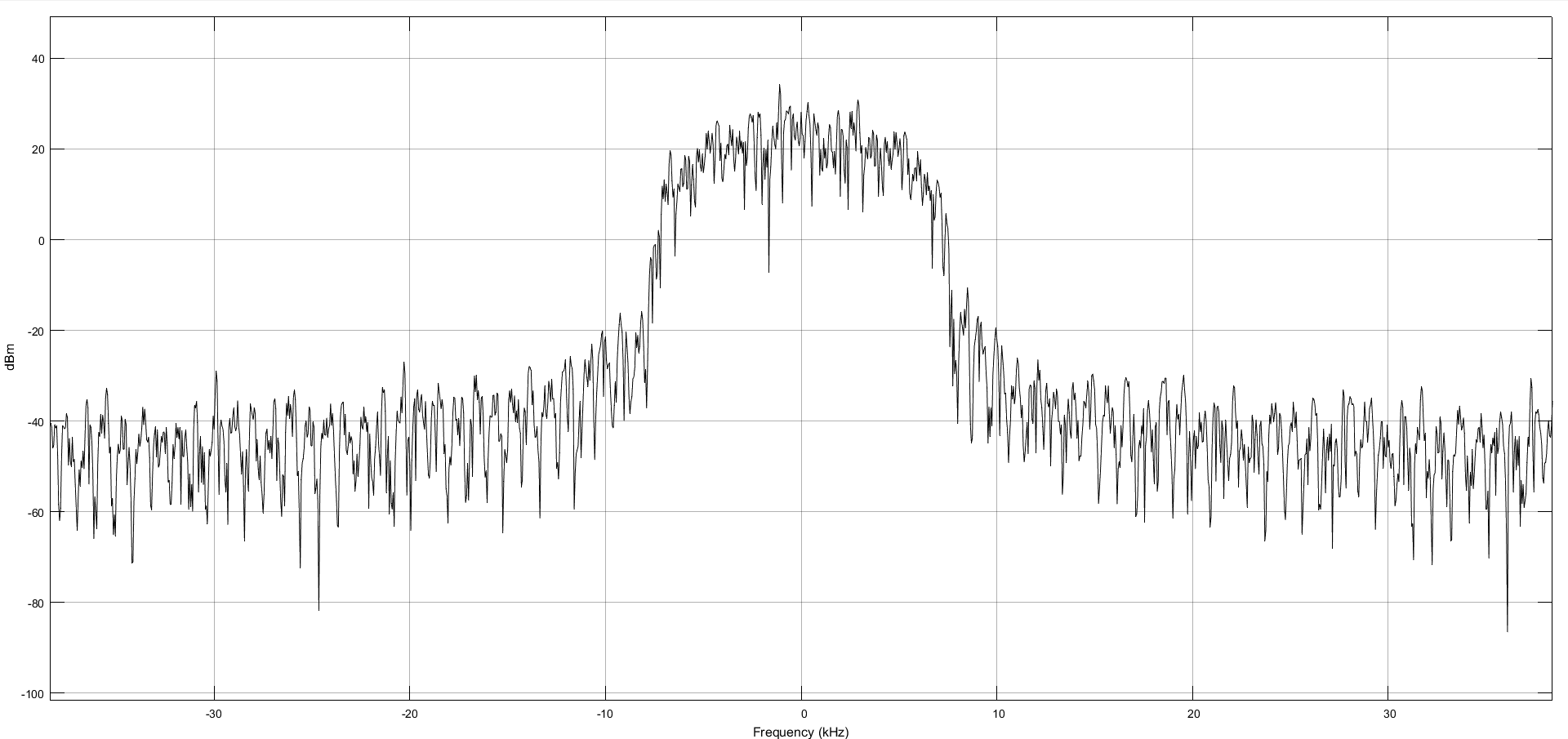
0.6
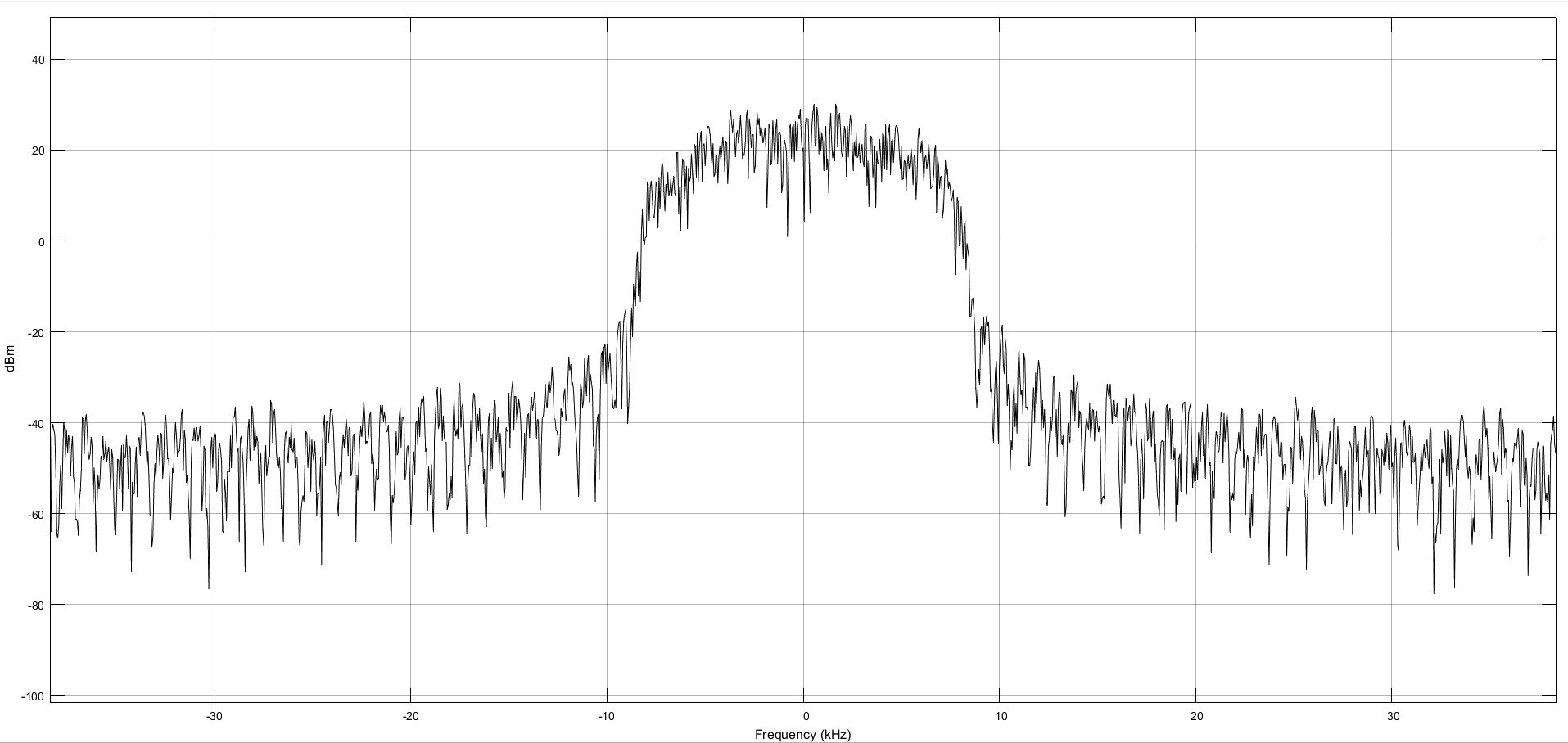
Рисунок 14 – Спектр при 0.8.
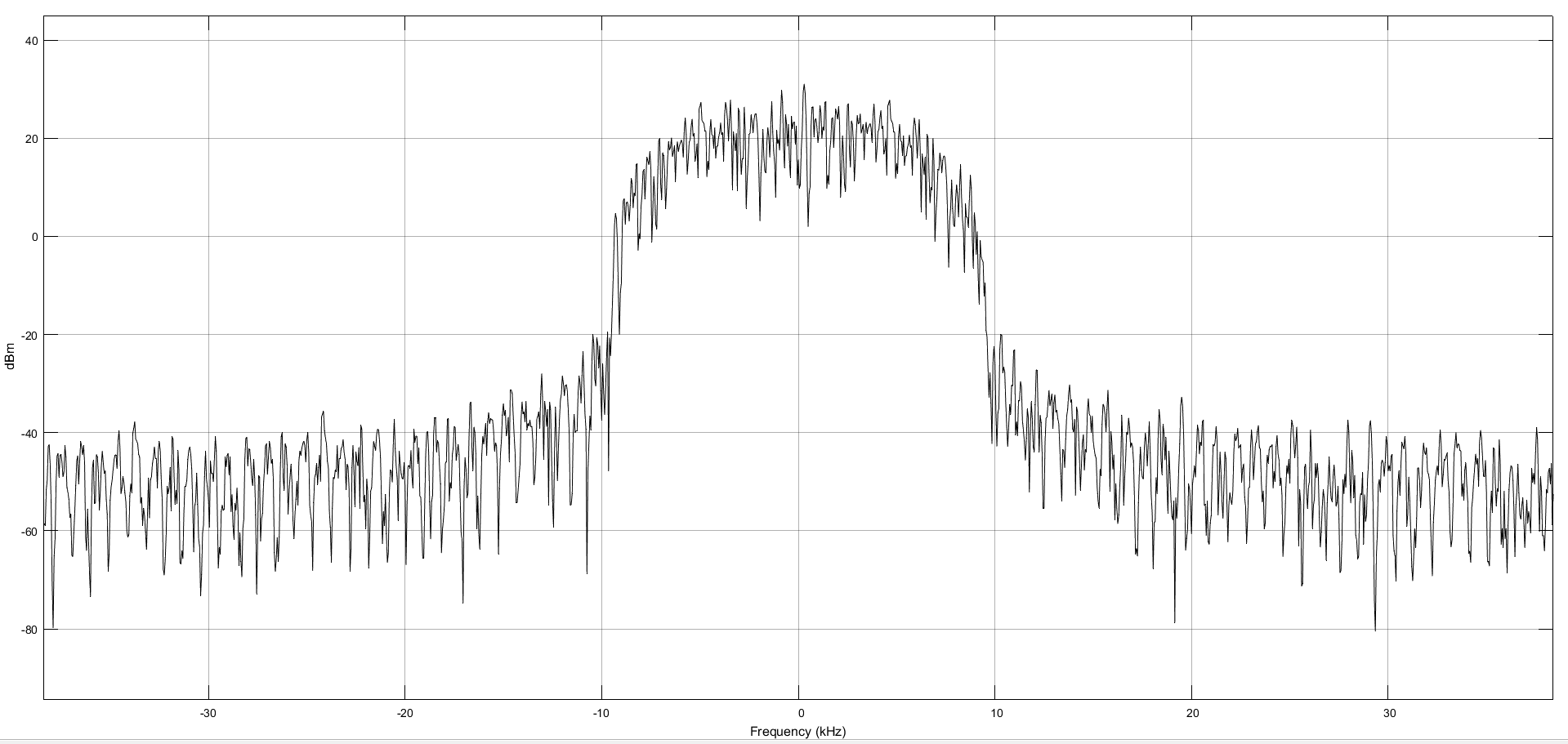
Рисунок 15 – Спектр при коэф. 1.
Далее по заданию нам необходимо определить из спектров сигнала его ширину. Шириной спектра сигнала называется интервал частот f =
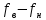, в котором содержится наибольшая часть энергии (мощности) сигнала. Из рисунков спектров видно, что наибольшая мощность находиться на холме, который имеет скаты, именно его нам и надо измерить. Для этого используем курсоры, которые установил по обе стороны от вершины холма, и занесем полученный результат в таблицу 1.После чего также с помощью курсоров замерим крутизну скатов…
Уровень относительно ширины спектра ( а не относительно нуля).
Таблица 1.
| Коэффициент скругления | Ширина спектра кГц | Крутизна скатов кГц | Уровень первого бокового лепестка |
| 0 | 9,8 | 6,5 (60/1) | 20 |
| 0.2 | 10,3 | 6,6 | 25 (-5) |
| 0.4 | 11,5 | 6,7 (60/3) | 33(-13) |
| 0.6 | 12,2 | 8 (60/3,5) | 35 (-15) |
| 0.8 | 14 | 11,8 (60/4 (4,3) | 40 (-20) |
| 1 | 15 | 12,6 (60/6) | 45 (-25) |
При помощи осциллографа оцените амплитуду квадратурных составляющих для внешних точек сигнального созвездия (точек с максимальной амплитудой) и для внутренних (точек с минимальной амплитудой). Занесите полученные данные в таблицу, найдите отношение максимального значения к минимальному
Уровень с в ручную на оригинальном.
Определяла с помощью второго температурного режима ( ширину и крутизну).
Чем больше коэффициент скругления, тем шире спектр и больше крутизна скатов (наверное)?
Фотографии при всех коэффициентов вставлять или как?
Выводы.