Задача

Проанализируйте данные зависимости успеваемости (балл в сессию) магистрантов группы ЭКмз-1501 в весеннюю сессию 2015-2016 учебного года по курсу «Статистика» от пропущенных ими занятий во 2-ом семестре (таблица 1). Изобразите графически зависимость успеваемости магистрантов, предварительно проранжировав значения х в порядке возрастания.

Таблица 1

Номер магистранта	Балл в сессию, у	Количество пропущенных занятий, х
1	5	1
2	3	8
3	4	3
4	4	5
5	3	8
6	2	10
7	5	2
8	4	4
9	5	2
10	3	6

Решение:

1. Ранжируем значения х в порядке возрастания:

Количество пропущенных занятий, х	Балл в сессию, у
1	5
2	5
2	5
3	4
4	4
5	4
6	3
8	3
8	3
10	2

Как видно из данных таблицы, чем меньше количество пропущенных занятий, тем выше балл, полученный магистрантами.

2. Изображаем графически зависимость успеваемости магистрантов от количества пропущенных занятий:



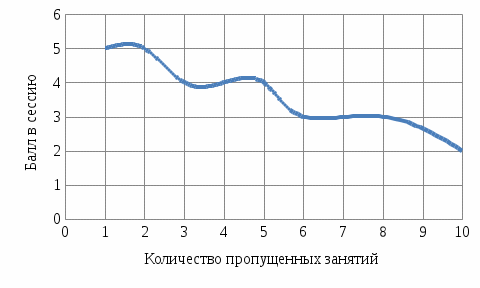
График также демонстрирует: чем меньше количество пропущенных занятий, тем выше балл, полученный магистрантами.

---

3. Проводим анализ корреляционных связей между показателями У, Х.

Для расчета линейного (парного) коэффициента корреляции осуществляем вспомогательные расчеты:

N	X	Y	X2	XY	Y2
1	1	5	1	5	25
2	2	5	4	10	25
3	2	5	4	10	25
4	3	4	9	12	16
5	4	4	16	16	16
6	5	4	25	20	16
7	6	3	36	18	9
8	8	3	64	24	9
9	8	3	64	24	9
10	10	2	100	20	4
Итого	49	38	323	159	154

Рассчитываем коэффициент парной линейной корреляции:





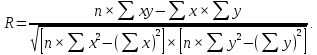
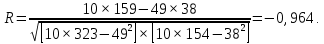
Коэффициент корреляции принимает значения от -1 до +1. Положительное его значение свидетельствует о наличии прямой связи, отрицательное – об обратной. Итак, в данном случае имеет место обратная связь, т.е. чем меньше Х (количество прогулов), тем больше У (успеваемость).

Абсолютная величина R, лежащая между 0 и 1, служит мерой тесноты связи. В зависимости от величины R можно сделать следующие заключения о степени тесноты связи: 0<=R<0,2 – практически нет связи; 0,2<=R<0,5 – слабая (не тесная) связь; 0,5<=R<0,75 – средняя связь; 0,75<=R<0,95 – сильная (тесная) связь; 0,95<=R<1,00 – практически функциональная связь. Если R по абсолютной величине равен 1, это свидетельствует о том, что связь между признаками является функциональной, т.е. факторный признак полностью определяет результативный. Полученное значение коэффициента R=-0,964 свидетельствует о наличии сильной связи между факторным и результирующим показателем.

---

Коэффициент детерминации рассчитывается по формуле:



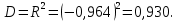
Полученное значение свидетельствует, что успеваемость магистрантов на 93,0% определяется посещаемостью занятий.

---

Смотрите также файлы

• 28. Южная Европа. Страны на Пиренейском полуострове.docx

• Регламентов подразделения хххххххххх.docx

• АйАру Балабашасы жшс арттарын ардатаан ел ардаты 1 азан арттар кніне арналан ісшара жоспары.docx

• за мерзімді жоспар блімі 3в онды блшектер жне олара амалдар олдану.docx

• Инструкция may 14, 2019.pdf