ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение квадратных уравнений специального вида
На сегодняшний день в базовой школьной программе по математике изучаются два основных метода решения квадратных уравнений. Это классический метод с использованием формул для корней (через дискриминант) и использование Теоремы Виета, которая позволяет угадать корни приведенного уравнения [1, с.209]. Предложенный нами способ является независимым относительно первых двух. С помощью него можно решать некоторые квадратные уравнения, удовлетворяющие специальным условиям. Будем рассматривать квадратное уравнение
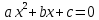.Теорема 1. Пусть квадратное уравнение
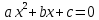таково, что 
. Тогда его корни можно найти по формулам
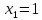
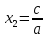
Доказательство. Проверим, что
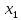и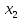 
действительно являются корнями данного квадратного уравнения.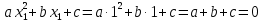
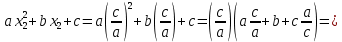
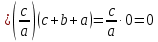
Таким образом,
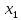и 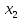являются корнями квадратного уравнения. Теорема доказана.Рассмотрим еще один частный случай, который позволяет решать квадратные уравнения специального вида устно.
Теорема 2. Пусть квадратное уравнение
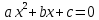таково, что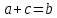
. Тогда его корни можно найти по формулам
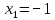
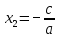
Доказательство. Для доказательства перепишем наше условие в виде
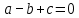
Проверим, что
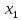и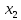 
действительно являются корнями данного квадратного уравнения.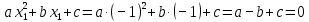
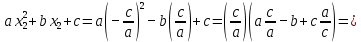
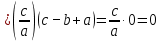
Таким образом, установлено, что
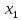и 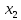являются корнями квадратного уравнения. Теорема доказана.Может показаться, что данные условия для квадратных уравнений на практике выполняются редко. Однако после проведенного анализа заданий, в которых необходимо решать квадратные уравнения (находить корни квадратного трехчлена), стало ясно, что примерно половина всех подобных заданий из основных учебников и задачников по алгебре удовлетворяют либо условию Теоремы 1 либо условию Теоремы 2, что подтверждает актуальность использования данного способа решения.
Список используемых источников:
1. Выгодский М.Я. Справочник по элементарной математике // Астрель. 2008. – 509, [3] с.:ил.
