Файл: Годфруа Ж. Что такое психология в 2х т. Оглавление предисловие редактора перевода.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 840
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Варианса = 
8. Наиболее употребительным показателем разброса служит стандартное отклонение,равное квадратному корню из вариансы. Таким образом, это квадратный корень из суммы квадратов всех отклонений от средней:
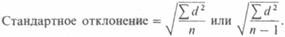
9. Важное свойство стандартного отклонения заключается в том. что независимо от его абсолютной величины в нормальном распределении оно всегда соответствует одинаковому проценту данных, располагающихся по обе стороны от средней: 68% результатов располагаются в пределах одного стандартного отклонения в обе стороны от средней. 95%-в пределах двух стандартных отклонений и 99,7%-в пределах трех стандартных отклонений.
10. С помощью перечисленных выше показателей можно осуществить оценку различий между двумя или несколькими распределениями, позволяющую проверить, насколько эти различия могут быть экстраполированы на популяцию, из которой взяты выборки. Для этого применяют методы индуктивной статистики.
II. Индуктивная статистика
1. Задача индуктивной статистикизаключается в том, чтобы оценить значимость тех различий, которые могут быть между двумя распределениями, с целью выяснить, можно ли распространить найденную закономерность на всю популяцию, из которой были взяты выборки.
2. Для того чтобы определить, достоверны ли различия между распределениями, следует выдвинутьгипотезу,которую нужно будет затем проверить статистическими методами. Нулевой гипотезойназывают предположение, согласно которому различие между распределениями недостоверно, тогда какальтернативная гипотезаутверждает противоположное.
3. В том случае, если данных достаточно,если эти данные количественныеи подчиняютсянормальному распределению,для проверки гипотез используют параметрические критерии.Если же данных мало либо они являются порядковымиили качественными(см. дополнение Б.1), используют непараметрическиекритерии.
4. Из параметрическихкритериев наиболее эффективен и чаще всего используется критерийtСтьюдента. Этот критерий позволяет сравнить средние и стандартные отклонения для двух распределений. В случае если эти показатели принадлежат независимым выборкам, используют формулу

Для сопряженных выборок используют иную формулу:
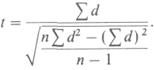
5. Если необходимо сравнить три или большее число распределений, используют иной параметрическийметод.-дисперсионный анализ.При этом с помощью метода Шеффе можно выявить пары выборок, различия между которыми достоверны либо недостоверны.
6. Критерий c2 (хи-квадрат) - это непараметрический критерий, позволяющий проверить, являются ли две переменные независимыми друг от друга. По этому методу сравнивают, как распределяются эмпирические частоты в зависимости от критериев для каждой переменной, с тем, как они распределились бы теоретически, если бы переменные были независимыми. Далее с помощью таблицы, в которую сводятся все частоты, вычисляют критерий c2. Для этого сначала находят разницу между каждой эмпирической (Э) и соответствующей теоретической (Т) частотой, а затем сумму этих разностей:
c2 = a
7. Критерий знаков(биномиальный тест) - еще один непараметрический метод, позволяющий легко определить, оказала ли независимая переменная существенное влияние по сравнению с исходным уровнем (фоном). Для этого сначала подсчитывают число «ухудшений» (-) или число «улучшений» ( + ), а затем сравнивают одно из этих двух чисел с тем, что могло бы получиться в результате чистой случайности (1 шанс из 2, или n/2). Для этого применяют формулу

8. Существуют и другие непараметрические тесты, которые приходится использовать для проверки гипотез тогда, когда нельзя применить параметрические критерии. К этим методам, в частности, относитсякритерий рангов,позволяющий определить, случайна или нет очередность событий в той или иной последовательности, а также критерийUи критерий Т.Последние два критерия используют в случае порядковых переменных соответственно для независимых и зависимых выборок.
9. Какой бы критерий ни использовался, его вычисленное значение следует сравнить с табличным для уровня значимости 0,05 с учетом числа степеней свободы. Если при этом вычисленный результат окажется выше, нулевая гипотеза может быть отвергнута и можно, следовательно, утверждать, что разница достоверна.
III. Корреляционный анализ
1. Задача корреляционного анализазаключается в том, чтобы установить возможную связь между двумя показателями, полученными на одной и той же или на двух различных выборках. При этом устанавливается, приводит ли увеличение какого-либо показателя к увеличению или уменьшению другого показателя.
2. Коэффициент корреляцииколеблется в пределах от +1, что соответствует полной положительной корреляции, до — 1 в случае полной отрицательной корреляции. Если этот коэффициент равен 0, то никакой корреляции между двумя рядами данных нет.
3. Коэффициент корреляции Браве - Пирсона (r)-этопараметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений. При этом используют формулу
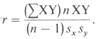
4. Коэффициент корреляции ранговСпирмена (rs)- этонепараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измерений.
5. Коэффициент корреляции может быть значимым лишь при достаточном числе пар данных, взятых в анализ. Это можно проверить с помощью таблицы пороговых значений rили rsдля уровня значимости 0,05.
Различие между данными контрольной и опытной группы после воздействия (критерий tдля независимых выборок):
t=3,11; h = 28; р <0,05; достоверно.
Различие между данными до и после воздействия для опытной группы (критерий tдля зависимых выборок):
t= - 8,14: h = 14; р <0,05; достоверно.
Сравнение показателей эффективности и времени реакции для опытной группы после воздействия (коэффициент r Браве-Пирсона):
r= -0,48; h = 13; р >0,05; недостоверно.
Сравнение показателей эффективности и времени реакции для контрольной группы после воздействия (коэффициент
rsСпирмена):
rs = + 0,73; h = 13; р <0,05; достоверно.


Примечания.1) Для больших выборок или уровня значимости меньше 0,05 следует обратиться к таблицам в пособиях по статистике.
2) Таблицы значений других непараметрических критериев можно найти в специальных руководствах (см. библиографию).
Chatillon G.,1977. Statistique en Sciences humaines, Trois-Rivieres, Ed. SMG.
Gilbert N.,1978. Statistiques, Montreal, Ed. HRW.
Moronev M.J.,1970. Comprendre la Statistique, Verviers, Gerard et Cie.
Siege/ S.,1956. Non-parametric Statistic, New York, MacGraw-Hill Book Co.
8. Наиболее употребительным показателем разброса служит стандартное отклонение,равное квадратному корню из вариансы. Таким образом, это квадратный корень из суммы квадратов всех отклонений от средней:
9. Важное свойство стандартного отклонения заключается в том. что независимо от его абсолютной величины в нормальном распределении оно всегда соответствует одинаковому проценту данных, располагающихся по обе стороны от средней: 68% результатов располагаются в пределах одного стандартного отклонения в обе стороны от средней. 95%-в пределах двух стандартных отклонений и 99,7%-в пределах трех стандартных отклонений.
10. С помощью перечисленных выше показателей можно осуществить оценку различий между двумя или несколькими распределениями, позволяющую проверить, насколько эти различия могут быть экстраполированы на популяцию, из которой взяты выборки. Для этого применяют методы индуктивной статистики.
II. Индуктивная статистика
1. Задача индуктивной статистикизаключается в том, чтобы оценить значимость тех различий, которые могут быть между двумя распределениями, с целью выяснить, можно ли распространить найденную закономерность на всю популяцию, из которой были взяты выборки.
2. Для того чтобы определить, достоверны ли различия между распределениями, следует выдвинутьгипотезу,которую нужно будет затем проверить статистическими методами. Нулевой гипотезойназывают предположение, согласно которому различие между распределениями недостоверно, тогда какальтернативная гипотезаутверждает противоположное.
3. В том случае, если данных достаточно,если эти данные количественныеи подчиняютсянормальному распределению,для проверки гипотез используют параметрические критерии.Если же данных мало либо они являются порядковымиили качественными(см. дополнение Б.1), используют непараметрическиекритерии.
4. Из параметрическихкритериев наиболее эффективен и чаще всего используется критерийtСтьюдента. Этот критерий позволяет сравнить средние и стандартные отклонения для двух распределений. В случае если эти показатели принадлежат независимым выборкам, используют формулу

Для сопряженных выборок используют иную формулу:
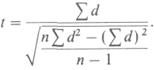
5. Если необходимо сравнить три или большее число распределений, используют иной параметрическийметод.-дисперсионный анализ.При этом с помощью метода Шеффе можно выявить пары выборок, различия между которыми достоверны либо недостоверны.
6. Критерий c2 (хи-квадрат) - это непараметрический критерий, позволяющий проверить, являются ли две переменные независимыми друг от друга. По этому методу сравнивают, как распределяются эмпирические частоты в зависимости от критериев для каждой переменной, с тем, как они распределились бы теоретически, если бы переменные были независимыми. Далее с помощью таблицы, в которую сводятся все частоты, вычисляют критерий c2. Для этого сначала находят разницу между каждой эмпирической (Э) и соответствующей теоретической (Т) частотой, а затем сумму этих разностей:
c2 = a
7. Критерий знаков(биномиальный тест) - еще один непараметрический метод, позволяющий легко определить, оказала ли независимая переменная существенное влияние по сравнению с исходным уровнем (фоном). Для этого сначала подсчитывают число «ухудшений» (-) или число «улучшений» ( + ), а затем сравнивают одно из этих двух чисел с тем, что могло бы получиться в результате чистой случайности (1 шанс из 2, или n/2). Для этого применяют формулу

8. Существуют и другие непараметрические тесты, которые приходится использовать для проверки гипотез тогда, когда нельзя применить параметрические критерии. К этим методам, в частности, относитсякритерий рангов,позволяющий определить, случайна или нет очередность событий в той или иной последовательности, а также критерийUи критерий Т.Последние два критерия используют в случае порядковых переменных соответственно для независимых и зависимых выборок.
9. Какой бы критерий ни использовался, его вычисленное значение следует сравнить с табличным для уровня значимости 0,05 с учетом числа степеней свободы. Если при этом вычисленный результат окажется выше, нулевая гипотеза может быть отвергнута и можно, следовательно, утверждать, что разница достоверна.
III. Корреляционный анализ
1. Задача корреляционного анализазаключается в том, чтобы установить возможную связь между двумя показателями, полученными на одной и той же или на двух различных выборках. При этом устанавливается, приводит ли увеличение какого-либо показателя к увеличению или уменьшению другого показателя.
2. Коэффициент корреляцииколеблется в пределах от +1, что соответствует полной положительной корреляции, до — 1 в случае полной отрицательной корреляции. Если этот коэффициент равен 0, то никакой корреляции между двумя рядами данных нет.
3. Коэффициент корреляции Браве - Пирсона (r)-этопараметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений. При этом используют формулу
4. Коэффициент корреляции ранговСпирмена (rs)- этонепараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измерений.
5. Коэффициент корреляции может быть значимым лишь при достаточном числе пар данных, взятых в анализ. Это можно проверить с помощью таблицы пороговых значений rили rsдля уровня значимости 0,05.
Результаты вычислений, которые предложено было сделать читателям
Различие между данными контрольной и опытной группы после воздействия (критерий tдля независимых выборок):
t=3,11; h = 28; р <0,05; достоверно.
Различие между данными до и после воздействия для опытной группы (критерий tдля зависимых выборок):
t= - 8,14: h = 14; р <0,05; достоверно.
Сравнение показателей эффективности и времени реакции для опытной группы после воздействия (коэффициент r Браве-Пирсона):
r= -0,48; h = 13; р >0,05; недостоверно.
Сравнение показателей эффективности и времени реакции для контрольной группы после воздействия (коэффициент
rsСпирмена):
rs = + 0,73; h = 13; р <0,05; достоверно.
Дополнение Б.5. Таблицы


Примечания.1) Для больших выборок или уровня значимости меньше 0,05 следует обратиться к таблицам в пособиях по статистике.
2) Таблицы значений других непараметрических критериев можно найти в специальных руководствах (см. библиографию).
Литература
Chatillon G.,1977. Statistique en Sciences humaines, Trois-Rivieres, Ed. SMG.
Gilbert N.,1978. Statistiques, Montreal, Ed. HRW.
Moronev M.J.,1970. Comprendre la Statistique, Verviers, Gerard et Cie.
Siege/ S.,1956. Non-parametric Statistic, New York, MacGraw-Hill Book Co.

