Министерство образования Российской федерации


ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)


Кафедра автоматизированных систем управления (АСУ)
ОТЧЕТ

По лабораторной работе № 1

по дисциплине «Основы теории управления»

Выполнил:

Студент__________

230105

28.03.2008

2008

1. ЦЕЛЬ РАБОТЫ
Целью лабораторной работы является изучение и приобретение практических навыков работы с моделями и частотными и переходными характеристиками типовых динамических звеньев систем управления.
2. ОСНОВНЫЕ СООТНОШЕНИЯ
В общем случае какой-либо объект в теории автоматического управления описывается передаточной функцией, содержащей полиномы от р произвольного порядка в числителе и знаменателе. Если передаточная функция объекта содержит простой множитель только в числителе либо в только в знаменателе, то такой объект называется типовым динамическим звеном.

К
лассификацию типовых звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения

Значения коэффициентов уравнения (1) и названия для наиболее часто встречающихся звеньев приведены в таблице 1.

Как известно, звенья, у которых коэффициенты а2  0 и b1  0 , обладают статизмом, т.е. однозначной связью между входной и выходной переменными в статическом режиме.

Другие виды звеньев, у которых коэффициенты а2  0, а1  0 и а0 0, обладают инерционностью (замедлением).

Таблица 1

№ п.п.	Наименование звена	a0	a1	a2	b0	b1	Примечания
1 2 3 4 5 6 7 8	Безынерционное (пропорциональное) Инерционное 1-го порядка (апериодическое) Инерционное 2-го порядка (апериодическое) Инерционное 2-го порядка (колебательное) Идеальное интегрирующее Реальное интегрирующее Идеальное дифференцирующее Реальное дифференцирующее	0 0 T22 T22 0 T 0 0	0 T T1 T1 1 1 0 T	1 1 1 1 0 0 1 1	0 0 0 0 0 0 k k	k k k k k k 0 0	T1 ≥ 2T2 T1 < 2T2

---

3. РЕЗУЛЬТАТЫ РАБОТЫ
Классификацию типовых звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения.
Пропорциональное (безынерционное) звено описывается уравнением



и имеет передаточную функцию

.

Параметр k называется коэффициентом передачи звена и может иметь любую размерность.

Инерционное (апериодическое) звено 1-го порядка

Описывается дифференциальным уравнением вида



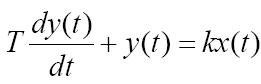
Перейдя к изображениям, была получена передаточная функция


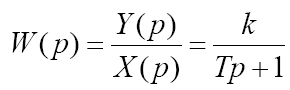
Идеальное дифференцирующее звеноописывается уравнением



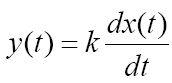
а его передаточная функция имеет вид

.

Идеальное интегрирующее звеноописывается таким уравнением



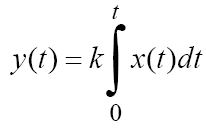
причём передаточная функция представима в виде



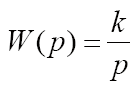
Реальное дифференцирующее звено

Такое звено является последовательным соединением дифференцирующего и инерционного звеньев, а его передаточная функция имеет вид


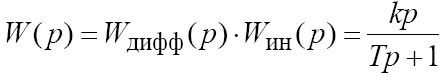
Инерционное апериодическое звено 2-го порядка

В общем случае звено второго порядка описывается уравнением



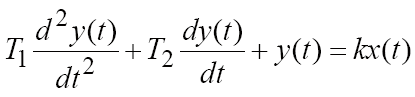
Передаточная функция апериодического звена 2-го порядка имеет вид



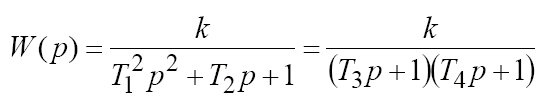
где

.

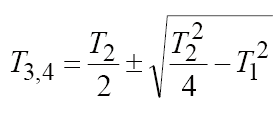Из выражения передаточной функции такого типа звена видно, что апериодическое звено второго порядка состоит из двух инерционных (апериодических) звеньев с эквивалентными постоянными времени Т

---

₃, Т₄, поэтому логарифмические частотные характеристики этих инерционных звеньев складываются.
Инерционное колебательное звено 2-го порядка

Это звено получается при комплексных сопряжённых полюсах передаточной функции. Передаточную функцию звена удобнее записать в виде:



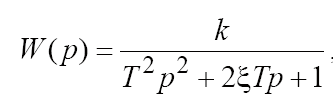
причём при 0 < ξ < 1 звено колебательное, а при ξ ≥ 1 звено уже является апериодическим 2-го порядка.

В данной работе были рассмотрены все эти типы динамических типовых звеньев. Коэффициенты их уравнений представлены в таблице 2.
Таблица 2

№ п.п.	Наименование звена	a0	a1	a2	b0	b1	Примечания
1	Безинерционное (пропорциональное)	0	0	1	0	10
2	Инерционное 1-го порядка (апериодическое)	0	T = 0,1	1	0	10
3	Инерционное 2-го порядка (апериодическое)	T22 = 0,0016	T1= 0,1	1	0	10	T1  2T2
4	Инерционное 2-го порядка (колебательное)	T22 = 0,04	T1= 0,1	1	0	10	T1 < 2T2
5	Идеальное интегрирующее	0	1	0	0	10
6	Реальное интегрирующее	T = 0,1	1	0	0	10
7	Идеальное дифференцирующее	0	0	1	10	0
8	Реальное дифференцирующее	0	T = 0,1	1	10	0

---

Далее для каждого звена по его передаточной функции запишем операторное уравнение. Так как параметр k = 10 (коэффициент перед b₁), то операторные уравнения запишутся в виде:
Безынерционное (пропорциональное) звено

W(s) =

Инерционное 1-го порядка (апериодическое) звено

W(s) =

Инерционное 2-го порядка (апериодическое) звено

W(s) =

Инерционное 2-го порядка (колебательное) звено

W(s) =

Идеальное интегрирующее звено

W(s) =

Реальное интегрирующее звено

W(s) =

Идеальное дифференцирующее звено

W(s) =

Реальное дифференцирующее звено

W(s) =

Для инерционных звеньев по логарифмическим частотным характеристикам определяем частоты сопряжения и среза.
Инерционное 1-го порядка (апериодическое) звено

W(s)ср = 99,5 рад/с

Инерционное 2-го порядка (апериодическое) звено

W(s)ср = 70,93 рад/с

Инерционное 2-го порядка (колебательное) звено

W(s)ср = 16,48 рад/с

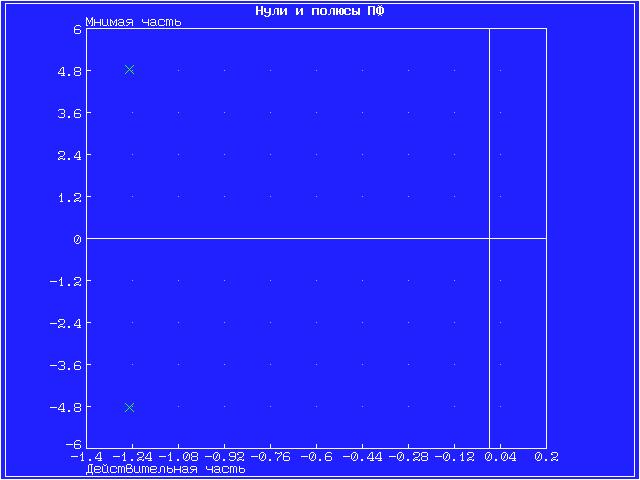
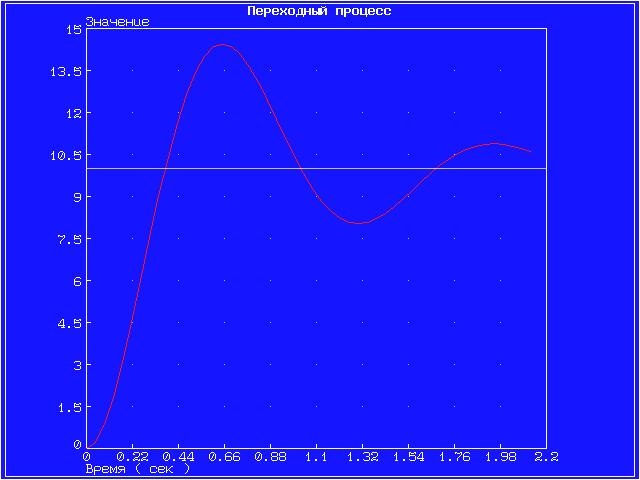
Значения полюсов и нулей передаточных функций, а также их влияние на переходный процесс, представлены на графиках ниже.

Инерционное 2-го порядка (апериодическое)

На графике представлены нули функции (крестиками).





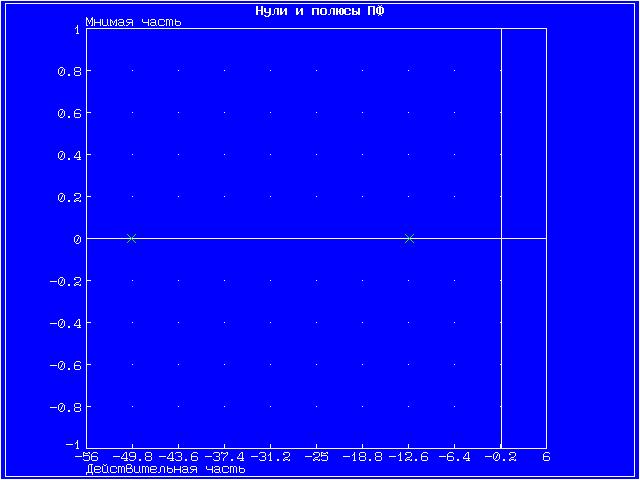
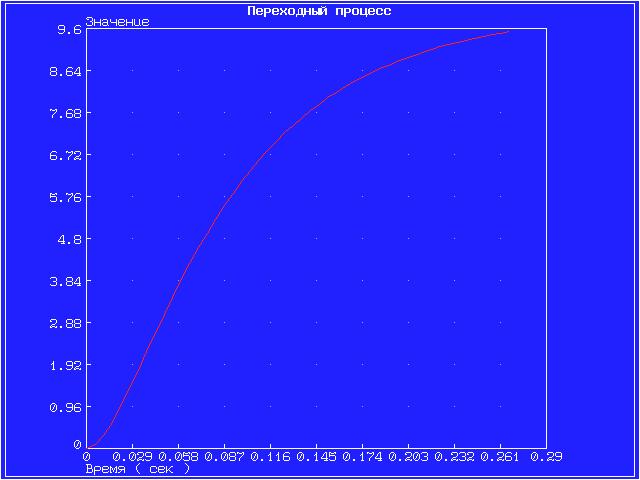
Инерционное 2-го порядка (колебательное)

На графике представлены полюсы функции.





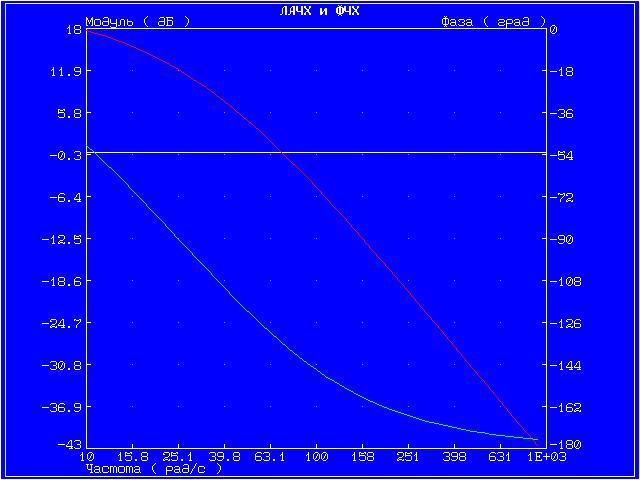
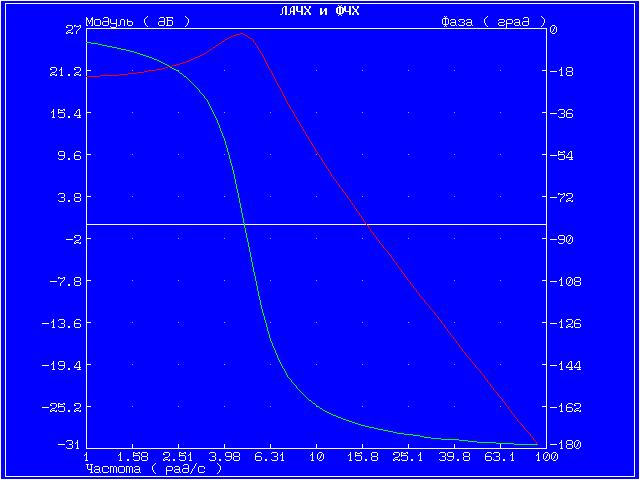
Графики амплитудной фазовой характеристики (АФХ), логарифмической амплитудной частотной характеристики (ЛАЧХ) и логарифмической фазовой частотной характеристики (ЛФЧХ).

---

Точная ЛАЧХ системы управления рассчитывается по формуле:



где А — коэффициент наклона ЛАХЧ.
Точная ЛФЧХ рассчитывается как сумма аргументов от АФХ звеньев, составляющих САУ, то есть:



где k — номер звена, n — общее количество звеньев САУ.
Графики ЛАЧХ и ЛФЧХ представлены на одной системе координат. Красный график — логарифмическая амплитудная частотная характеристика, зелёный график — логарифмическая фазовая частотная характеристика.

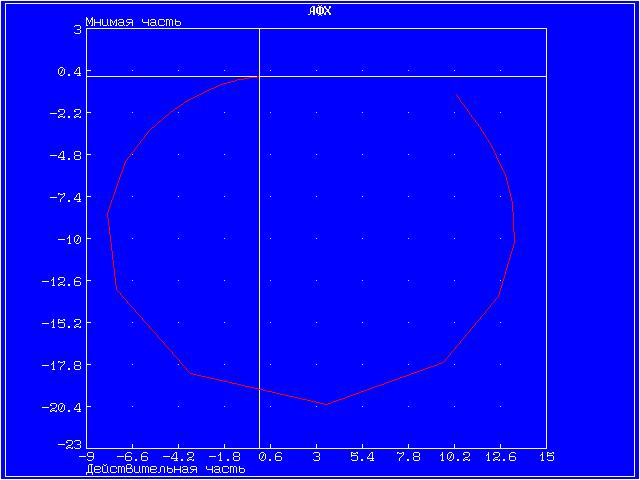
График амплитудной фазовой характеристики представлен на отдельном рисунке.
Инерционное 2-го порядка (апериодическое)




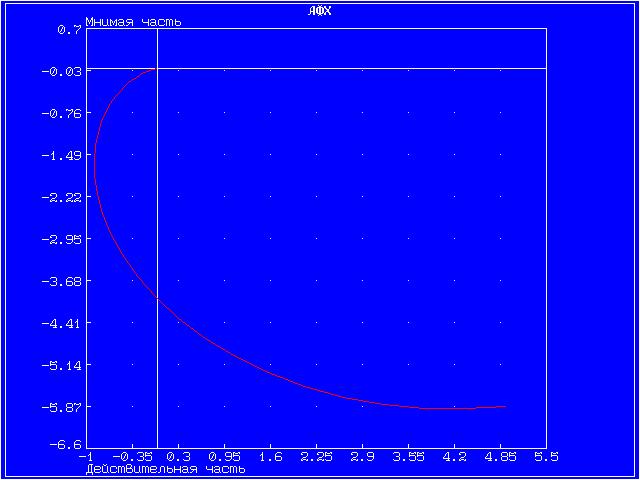
Инерционное 2-го порядка (колебательное)



4. ВЫВОДЫ

В результате проделанной работы были изучены модели восьми звеньев, но более подробно исследовались звенья 2-го порядка. Для звена по его передаточной функции записано операторное уравнение. Построены графики переходных функций и определены нули и полюсы динамического звена.

С помощью логарифмических частотных характеристик определены частоты среза и сопряжения.

Колебательное звено имеет более сложные характеристики и менее гладкие графики АФХ, ЛАЧХ, ЛФЧХ.

Колебания малых частот «пропускаются» звеном с отношением амплитуд выходной и входной величин, близким к статистическому коэффициенту передачи звена k. Колебания больших частот проходит с сильным ослаблением амплитуды.
5. ВОПРОСЫ

1. Что такое передаточная функция?

Любая система, которую можно возбудить гармоническими колебаниями, будет реагировать на них также каким-то колебательным движением.

Существует характеристика, которая определяет преобразование амплитуды и сдвиг фазы выходного колебания по отношению к входному. Такой характеристикой может быть следующее отношение

---

Смотрите также файлы

• 2. Основные понятия политической психологии.pdf

• Наименование дисциплины на русском языке Наименование дисциплины на английском языке.docx

• Тест Самооценка психических состояний (по Айзенку).docx

• Материалом для подготовки устного высказывания могут служить готовые темы, которые можно найти в учебных пособиях.docx

• Тсінік хат Математикаоупні.docx