У газов, близких по своим свойствам к идеальному газу теплоемкость при постоянном объеме в широких температурных интервалах практически не зависит от температуры: С_v=const.

C_p = С_v + R

Т.о. теплоемкость при постоянном давлении равна сумме теплоемкости при постоянном объеме и газовой постоянной. Но это соотношение справедливо только для идеального газа.

Отношение теплоемкостей



представляет собой характерную для каждого газа величину. Значение   определяется числом и характером степеней свободы молекул.

 откуда  .

3. 
   Какой процесс называется адиабатическим? Написать уравнение адиабатного процесса (уравнение Пуассона).
   

. Адиабати́ческий, или адиаба́тный[1] проце́сс (от др.-греч. ἀδιάβατος «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством.Перейти к разделу «#Физический смысл адиабатического процесса» Серьёзное исследование адиабатических процессов началось в XVIII веке[2].Перейти к разделу «#История» В целом термин адиабатический в разных областях науки всегда подразумевает сохранение неизменным какого-то параметра. Так в квантовой химии, электронно адибатический процесс это процесс, в котором не изменяется квантовое число электронного состояния. Например, молекула всегда остается в первом возбужденном состоянии вне зависимости от изменения положения атомных ядер. Соответственно неадиабатическим называется процесс, в котором происходит изменение какого-то важного параметраВ термодинамике, адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[3]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Равновесный адиабатный процесс является изоэнтропным процессом[4]. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы[5].Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона.Перейти к разделу «#Уравнение Пуассона для идеального газа» Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Также такие процессы получили ряд применений в технике.

---

Уравнение Пуассона описывает адиабатный процесс, протекающий в идеальном газе. Адиабатным называют такой процесс, при котором отсутствует теплообмен между рассматриваемой системой и окружающей средой:   .

Уравнение Пуассона имеет вид:

4. 
   Сформулировать и записать 1-вое начало термодинамики. Что понимают под внутренней энергией: а) реального газа; б) идеального газа.
   

Пе́рвое нача́ло термодина́мики (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические, массообменные и химические процессы[1][2][3]. В форме закона сохранения (уравнения баланса энергии) первое начало используют в термодинамике потока и в неравновесной термодинамике. В равновесной термодинамике под первым законом термодинамики обычно подразумевают одно из следствий закона сохранения энергии, из чего проистекает отсутствие единообразия формулировок первого начала, используемых в учебной и научной литературе (К. А. Путилов в своей монографии[4] приводит шесть формулировок, которые он считает наиболее удачными). Внутренняя энергия – это сумма энергий молекулярных взаимодействий и энергии теплового движения молекул.

В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема (закон Джоуля). Внутренняя энергия идеального газа определяется кинетической энергией теплового движения молекул и для одного моля вещества выражается формулой  . Внутренняя энергия реального газа включает в себя кинетическую энергию теплового движения молекул и потенциальную энергию их взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения молекул, обуславливающими внутреннее давление 

---

. Поэтому часть внутренней энергии, обусловленной межмолекулярным взаимодействием, может быть вычислена как работа,  совершаемая по преодолению сил внутреннего давления т.е.

,

откуда

.

Знак минус в этом выражении указывает, что межмолекулярные силы, создающие внутреннее давление, являются силами притяжения. С учетом обеих составляющих внутренняя энергия реального газа выражается в виде

,

она растет тс повышением температуры и увеличением объема.

Пусть газ из состояния с объемом  расширяется до объема   адиабатически в вакуум без совершения внешней работы. Тогда из выражения   получим

,

Т.е. при адиабатическом расширении без совершения работы внутренняя энергия газа не изменяется. Этот равенство формально справедливо и для идеальных и для реальных газов. Однако физический смысл этого равенства для обоих газов различен. Для идеального газа равенство  означает равенство температур  , при расширении идеального газа в вакуум его температура не изменяется. В случае реального газа с учетом

 и 

получим

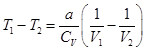.                                            (2.79)

 

При расширении V₂>V₁, поэтому  Т₁>Т₂. Реальный газ при адиабатическом расширении в вакуум охлаждается, при сжатии нагревается.

---

Внутренняя энергия тела - это полная энергия всех молекул, которые его составляют. Внутренняя энергия идеального газа пропорциональна его температуре.

U = 3/2 · ν · R · T.

Чтобы изменить внутреннюю энергию вещества, надо сообщить ему некоторое количество тепла или совершить работу.

Работа в термодинамике равна изменению внутренней энергии системы: A = ΔU.

Работа газа в изобарном процессе равна A = P · ΔV.

5. 
   Что такое внутренняя энергия? Почему ее называют функцией состояния?
   

внутренняя энергия – это физическая величина, равная сумме кинетической энергии теплового движения частиц тела и потенциальной энергии их взаимодействия друг с другом. Обозначение – ​ (U) ​, в СИ единица измерения – Джоуль (Дж). В термодинамике внутренняя энергия зависит от температуры и объема тела. Внутренняя энергия тел зависит от их температуры, массы и агрегатного состояния.

Функция состояния-это свойство, описывающее определенное состояние, независимо от пути, пройденного для достижения этого состояния. Напротив, функции, значение которых зависит от пути, пройденного для перехода между двумя состояниями, называются путями функции.

6. 
   Что такое теплота? Почему ее называют функцией процесса?
   

. Теплота есть одна из форм передачи энергии от одного тела к другому. В 1842 г. немецкий ученый Р. Майер открыл закон эквивалентности между теплотой и работой, который является частным случаем первого начала термодинамики: взаимное превращение теплоты и работы совершается в строго эквивалентном соотношении:

.

Обе эти величины должны быть выражены в одинаковых единицах.

Вернёмся к уравнению первого начала термодинамики (6.1). В этом уравнении теплота ( ) является алгебраической суммой двух величин   и  , причём одна из них ( ) является функцией процесса, а это значит, что теплота может быть только функцией процесса.

---

Таким образом, хотя три величины, входящие в уравнение первого начала термодинамики, измеряются в одинаковых единицах, тем не менее, по своим свойствам эти величины глубоко различны.

Теплота и работа зависят от промежуточных состояний рабочего тела в процессе, поэтому должны определяться по формулам, в которых учитывается характер рассматриваемого процесса.

Функции состояния не зависят от промежуточных состояний рабочего тела, поэтому могут подсчитываться по одной общей для них формуле.

7. 
   Определить Сp/С_V в зависимости от степеней свободы.
   

Cv= (i/2)R Cp= ((i+2)/2)R i- число степеней свободы

---

Смотрите также файлы

• Правила безопасного поведения воспитанников на воде, у водоема (в бассейне, плескательнице) Правила безопасного поведения воспитанников.doc

• Правила безопасного поведения воспитанников на занятиях, при работе с инструментами и предметами Правила безопасного поведения на занятиях.doc

• Учебнометодическое пособие по дисциплине информационная экология для студентов 3 курса цзопб.pdf

• Главной задачей фгос третьего поколения заявлена конкретизация требований к обучающимся. Дело в том, что в предыдущей редакции Стандарт включал только общие установки на формирование определённых компетенций.docx

• Статья 1 Кодекса рф об административных правонарушениях формулирует официальное (легальное) определение административного правонарушения, под которым признается противоправное,.docx