ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 25
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Хикматуллоев Р. Ж.
Вариант 12
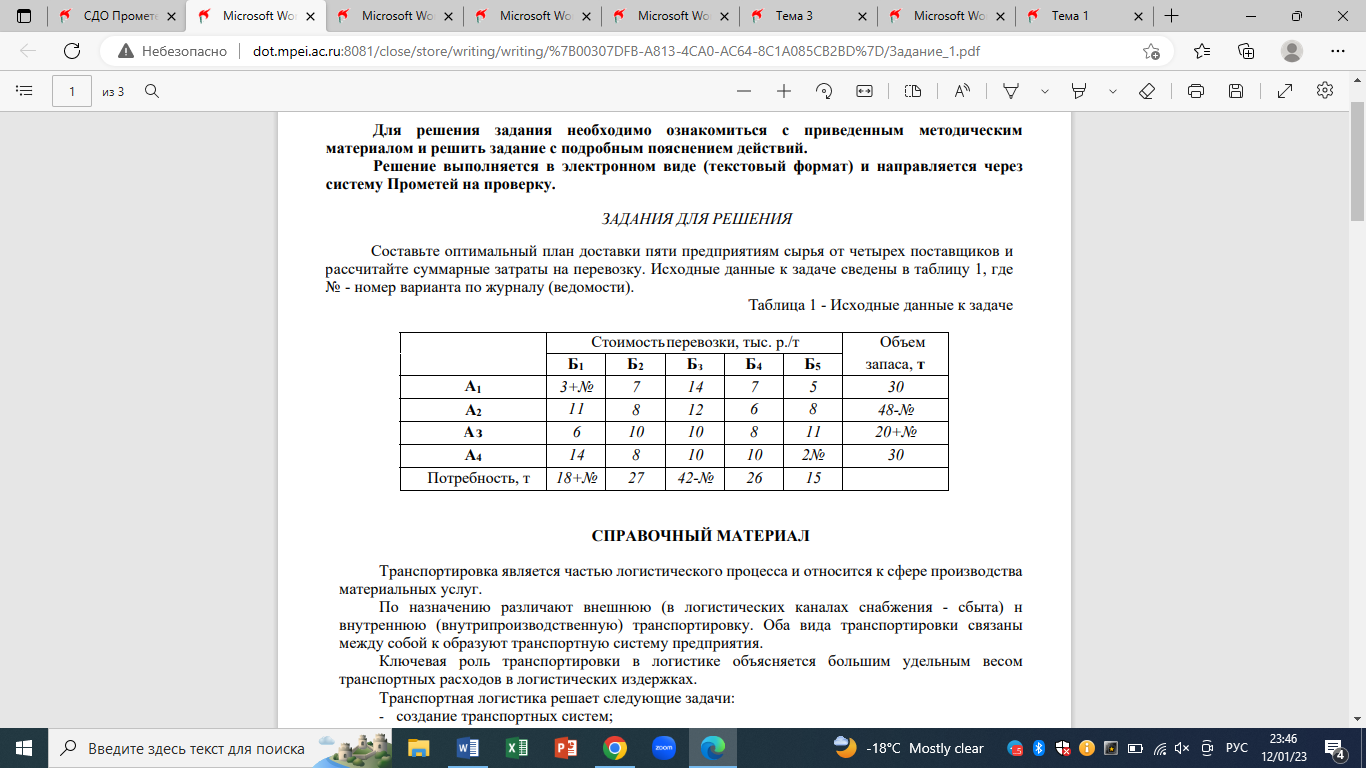
Составьте оптимальный план доставки пяти предприятиям сырья от четырех поставщиков и рассчитайте суммарные затраты на перевозку. Исходные данные к задаче сведены в таблицу 1, где № - номер варианта по журналу (ведомости).
Решение
| | Б1 | Б2 | Б3 | Б4 | Б5 | объем |
| А1 | 3+12 | 7 | 14 | 7 | 5 | 30 |
| А2 | 11 | 8 | 12 | 6 | 8 | 48-12 |
| А3 | 6 | 10 | 10 | 8 | 11 | 20+12 |
| А4 | 14 | 8 | 10 | 10 | 20+12 | 30 |
| потребность | 18+12 | 27 | 42-12 | 26 | 15 | |
| | Б1 | Б2 | Б3 | Б4 | Б5 | объем |
| А1 | 15 | 7 | 14 | 7 | 5 | 30 |
| А2 | 11 | 8 | 12 | 6 | 8 | 36 |
| А3 | 6 | 10 | 10 | 8 | 11 | 32 |
| А4 | 14 | 8 | 10 | 10 | 32 | 30 |
| потребность | 30 | 27 | 30 | 26 | 15 | |
Решение задачи начинается с составления опорного плана перевозки методом «северо-западного» угла, т.е. начиная с верхней левой клетки таблицы следующим образом. Предприятие Б1 подало заявку на 30 т груза. Удовлетворим её из запасов поставщика A1. После отправки на складе поставщика останется 30 - 30 = 0 т груза. Так как потребности предприятия Б1
полностью удовлетворены, вычеркнем из таблицы столбец Б1. Запасы поставщика А1 исчерпаны. Вычеркнем из таблицы строку A1.
Новым северо-западным углом теперь является клетка А2Б2. Предприятию Б2 необходимо отгрузить 27 т. Удовлетворим её из запасов поставщика A2. Так как потребности предприятия Б2 полностью удовлетворены, вычеркнем из таблицы столбец Б2.
В оставшейся части таблицы новым северо-западным углом будет клетка A2Б3. Направим остаток груза у поставщика A2 в количестве 36-27=9т потребителю Б3. По условиям задачи потребность Б3 составляет 30 т, следовательно, она еще не полностью удовлетворена. Однако запасы поставщика А2 исчерпаны. Вычеркнем из таблицы строку A2.
Новым северо-западным углом теперь является клетка А3Б3. Предприятию Б3 еще необходимо отгрузить 30-9=21 т груза. Удовлетворим её из запасов поставщика A3. Его запасы после отгрузки составят 32 - 21 = 11т, а потребность Б3 будет полностью удовлетворена. Так как потребности предприятия Б3 полностью удовлетворены, вычеркнем из таблицы столбец Б3.
В оставшейся части таблицы новым северо-западным углом будет клетка A3Б4. Направим остаток груза у поставщика A3 в количестве 32-21=11т потребителю Б4. По условиям задачи потребность Б4 составляет 26 т, следовательно, она еще не полностью удовлетворена. Однако запасы поставщика А3 исчерпаны. Вычеркнем из таблицы строку A3.
Новым северо-западным углом теперь является клетка А4Б4. Предприятию Б4 еще необходимо отгрузить 26-11=15 т груза. Удовлетворим её из запасов поставщика A4. Его запасы после отгрузки составят 30 - 15 = 15т, а потребность Б4 будет полностью удовлетворена. В оставшейся части таблицы новым северо-западным углом будет клетка A4Б5. Направим остаток груза у поставщика A4 в количестве 30-15=15т потребителю Б5. По условиям задачи потребность Б5 полностью удовлетворена.
Заполняем ее и получаем первый план перевозок в виде таблицы.
| | Б1 | Б2 | Б3 | Б4 | Б5 | объем | |||||
| А1 | 30 | 15 | - | 7 | - | 14 | - | 7 | - | 5 | 30 |
| А2 | - | 11 | 27 | 8 | 9 | 12 | - | 6 | - | 8 | 36 |
| А3 | - | 6 | - | 10 | 21 | 10 | 11 | 8 | - | 11 | 32 |
| А4 | - | 14 | - | 8 | - | 10 | 15 | 10 | 15 | 32 | 30 |
| потребность | 30 | 27 | 30 | 26 | 15 | | |||||
Проверим, является ли этот план допустимым и соответствует ли он ограничениям, существующим для подобного рода задач. План можно признать допустимым, если выполняются два условия: 1) Суммы перевозок по строкам равны запасам, а суммы перевозок по столбцам - потребностям, т.е. все заявки удовлетворены, а запасы израсходованы. 2) Число свободных клеток с нулевыми перевозками должно быть равно: (m – 1) • (n — 1) = 3 • 4 = 12, а число базисных клеток (заполненных) равно: (m + n — 1) = 4+ 5 — 1=8.
Условие не выполняется
Попробуем составить новый план.
Для этого, содержимое А3Б4=11т между А3Б4=10т и А3Б5=1т. Тогда чтобы было равенство А4Б4 станет 16т, а А4Б5 станет 14т.
| | Б1 | Б2 | Б3 | Б4 | Б5 | объем | |||||
| А1 | 30 | 15 | - | 7 | - | 14 | - | 7 | - | 5 | 30 |
| А2 | - | 11 | 27 | 8 | 9 | 12 | - | 6 | - | 8 | 36 |
| А3 | - | 6 | - | 10 | 21 | 10 | 10 | 8 | 1 | 11 | 32 |
| А4 | - | 14 | - | 8 | - | 10 | 16 | 10 | 14 | 32 | 30 |
| потребность | 30 | 27 | 30 | 26 | 15 | | |||||
Теперь условие выполняется.
Рассчитаем суммарные затраты на перевозку по формуле,
При первом варианте плана стоимость перевозки по формуле будет р
W= 30 • 15 + 27 • 8 + 9 • 12 + 21 • 10 + 10 • 8 + 16 • 10 + 1 • 11 + 14 • 32=1683 тыс. р.
По таблице видно, что есть пути сделать это дешевле, воспользуемся методом перестановок и получим новый план:
| | Б1 | Б2 | Б3 | Б4 | Б5 | объем | |||||
| А1 | - | 15 | 15 | 7 | - | 14 | - | 7 | 15 | 5 | 30 |
| А2 | - | 11 | 12 | 8 | - | 12 | 24 | 6 | - | 8 | 36 |
| А3 | 30 | 6 | - | 10 | 1 | 10 | 1 | 8 | - | 11 | 32 |
| А4 | - | 14 | - | 8 | 29 | 10 | - | 10 | - | 32 | 30 |
| потребность | 30 | 27 | 30 | 26 | 15 | | |||||
W= 30 • 6 + 15 • 7 + 12• 8 + 1 • 10 + 29 • 10 + 24 • 6 + 1 • 8 + 15 • 15=1058 тыс. р.
Дальнейшее улучшение уже невозможно. Таким образом, нам удалось снизить стоимость перевозки на 1683 - 1058 = 625 тыс. р.
