ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 55
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Общие вопросы теории цепей
Электрическая цепь — это совокупность генерирующих, приемных и вспомогательных устройств, соединенных между собой электрическими проводами.
Электрическая цепь делится на внутреннюю и внешнюю части. К внутренней части электрической цепи относится сам источник электрической энергии. Во внешнюю часть цепи входят соединительные провода, потребители, рубильники, выключатели, электроизмерительные приборы, т.е. все то, что присоединено к зажимам источника электрической энергии.
Электрический ток может протекать только по замкнутой электрической цепи. Разрыв цепи в любом месте вызывает прекращение электрического тока.
Под электрическими цепями постоянного тока в электротехнике подразумевают цепи, в которых ток не меняет своего направления, т. е. полярность источников ЭДС в которых постоянна.
Под электрическими цепями переменного тока подразумевают цепи, в которых протекает ток изменяющегося во времени.
Источники питания цепи постоянного тока - это гальванические элементы, электрические аккумуляторы, электромеханические генераторы, термоэлектрические генераторы, фотоэлементы и др.
Электроприемниками постоянного тока являются электродвигатели, преобразующие электрическую энергию в механическую, нагревательные и осветительные приборы, электролизные установки и др.
В качестве вспомогательного оборудования в электрическую цепь входят коммутационные аппараты защиты и управления, приборы для измерения электрических величин,
Электрическая схема – графическое изображение электрической цепи, в которой реальные элементы представлены их условными обозначениями.
Топологическая схема цепи – изображение ветвей в виде линий без изображения на них условных обозначений компонентов схемы.
Ветвью электрической цепи (схемы) называют участок цепи, через каждый компонент которого текущее значение тока в любой момент времени имеет одну и ту же величину. Ветвь может характеризоваться электрическим сопротивлением.
Узлом называют место соединения трёх или большего числа ветвей.
Контуром цепи называют любой замкнутый путь, включающий одну или несколько ветвей.
Двухполюсником называют любую часть цепи, имеющую два зажима или контакта для подключения к внешней схеме. Двухполюсник является активным, если содержит источники электрической энергии. Пассивный двухполюсник не содержит источников энергии.
Четырёхполюсником считают участок цепи, имеющий два входных и два выходных контакта. Подобно двухполюснику различают активный и пассивный четырёхполюсник.
Элементы электрической цепи. Под элементами в теории цепей понимают не реальные устройства, а их идеализированные модели, обладающие определенными свойствами реальных прототипов. Такими идеализированными элементами являются резистивный, индуктивный и емкостный элементы, а также независимые источники напряжения и тока.
  |  |  |
| Резистор – резистивный элемент, в котором происходит необратимый процесс преобразования электрической энергии в тепловую энергию т.е. вся энергия, поступающая от источника, потребляется активной нагрузкой с активным сопротивлением R – сопротивление [Ом] ; U – напряжение; I – ток | Катушка - индуктивный элемент, при протекании по ней тока обладает способностью создавать магнитное поле. Параметр катушки – индуктивность L, [Гн].Катушка обладает и активным сопротивлением ρ – удельное сопротивление материала проводника; l – длина проводника; s – сечение проводника; | Конденсатор – емкостный элемент, предназначенный для использования его ёмкости, в нем накапливается энергия электрического поля. Параметр элемента – емкость С, является коэффициентом пропорциональности между зарядом q и прикладываемым напряжением u; q, [Кл] кулон; С, [Ф] фарад u, [B] вольт |
Рис. 1.1. К определению элементов электрической цепи
ЗАДАНИЕ №1.
Для электрической цепи, схема которой изображена на рис. 1.1 – 1.50, по заданным в табл.1 параметрам и напряжению приложенному к цепи, определить токи во всех ветвях цепи. Определить активную, реактивную и полную мощности цепи. Построить в масштабе векторную диаграмму токов и напряжений.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Для правильного решения поставленной задачи необходимо изучить теорию электрических цепей однофазного синусоидального тока, усвоить основные формулы сопротивлений, проводимостей токов, напряжений; научиться применять для анализа и расчета закон Ома, уравнения Кирхгофа, метод проводимостей.
Все предлагаемые заданием электрические цепи являются смешанными, т.е. содержат последовательную ветвь и две параллельные. В каждой ветви имеются различные сопротивления, величины которых заданы.
Для примера рассмотрим обобщенную цепь, представленную на рис. 1.
ВНИМАНИЕ: РАСЧЕТ В ПРИМЕРЕ ДАЕТСЯ ТОЛЬКО ДЛЯ ЦЕПИ РИС.1
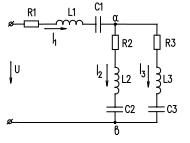
Общий ход решения задач подобного типа следующий. Необходимо преобразовать последовательно-параллельную цепь в простую последовательную цепь, заменив разветвленный участок цепи эквивалентной последовательной цепочкой.
Рис.1
Прежде всего, необходимо методом проводимости определить параметры эквивалентной цепочки, которой может быть замещен разветвленный участок цепи.
В эквивалентной цепочке реактивное сопротивление будет индуктивным или емкостным в зависимости от знака эквивалентной реактивной проводимости. Дальнейшее решение сводится к определению активного и реактивного сопротивления цепи, а по ним полного сопротивления цепи.
По каждому сопротивлению цепи и заданному напряжению определяется общий потребляемый ток в цепи. Чтобы определить ток в отдельных ветвях разветвленного участка, находим сначала напряжение между узловыми точками, а затем и токи в ветвях.
6
После чего находим напряжение на указанном участке, активную, реактивную и полную мощности в цепи. Заканчиваем расчет построением векторной диаграммы токов и напряжений.
Алгоритм расчета
-
Вычисляем величины сопротивлений отдельных элементов цепи:
XL = ω∙L = 2πf∙L,XC = 1/ω∙C = 1/ 2πf∙C
где f = 50 Гц, L – в Генри (Гн), С – в Фарадах (Ф).
ВНИМАНИЕ: в задании L дается в мГн, С – в мкФ.
-
Вычисляем полные сопротивления ветвей:
Z1 =
Z2 =
Z3 =
-
Вычисляем активные проводимости параллельных ветвей:
g2 = R2 / Z22 ,g3 = R3 / Z32 .
4. Вычисляем общую эквивалентную активную проводимостьgЭ:
gЭ = g2 +g3 .
-
Вычисляем реактивные проводимости ветвей и общую эквивалентную проводимость GЭ :
вL2 = XL2/ Z22 ,вC2= XC2 / Z22 ,
вL3 = XL3 / Z32 ,вC3 = XC3 / Z32 ,GЭ =
вL =вL2 + вL3 ,вC
