Федеральное государственное автономное образовательное

учреждение высшего образования

«Национальный исследовательский Нижегородский государственный

университет им. Н.И. Лобачевского»
Институт экономики и предпринимательства
Дата поступления контрольной работы:

Дата проверки:

Оценка:

Подпись преподавателя:
КОНТРОЛЬНАЯ РАБОТА

Вариант 2 по дисциплине статистика - ЭБ

Фамилия: Богдарина

Имя: Ульяна

Отчество: Дмитриевна

Группа: 1621Б3РТ1

№ зачетной книжки: 21160110

ФИО преподавателя: Матвеев Виктор Александрович

Нижний Новгород, 2023 г.

Контрольные задания 8.

1. Задача: Определить линейный коэффициент корреляции и построить уравнение регрессии, используя следующие статистические данные по промышленным предприятиям:

Оборотные средства, млн. р.	120	171	150	178	222	271	254	278	300	352
Выпуск продукции, млн. р.	10,9	7,8	13,1	12,4	13,4	17,1	23,1	23,5	29,6	33,1

Решение

Формально критерий МНК можно записать так:

S = ∑(yi - y^*i)² → min
Система нормальных уравнений.

a·n + b·∑x = ∑y

a·∑x + b·∑x² = ∑y·x
Для расчета параметров регрессии построим расчетную таблицу.

x	y	x2	y2	x*y
120	10.9	14400	118.81	1308
171	7.8	29241	60.84	1333.8
150	13.1	22500	171.61	1965
178	12.4	31684	153.76	2207.2
222	13.4	49284	179.56	2974.8
271	17.1	73441	292.41	4634.1
254	23.1	64516	533.61	5867.4
278	23.5	77284	552.25	6533
300	29.6	90000	876.16	8880
352	33.1	123904	1095.61	11651.2
2296	184	576254	4034.62	47354.5

---

Для наших данных система уравнений имеет вид:

10a + 2296·b = 184 (1)

2296·a + 576254·b = 47354.5 (2)
Умножим уравнение (1) системы на (-229.6), получим систему и решим её методом алгебраического сложения.
-2296a -527161.6 b = -42246.4

2296*a + 576254*b = 47354.5

2296*a -2296*a + 49092.4*b = 5108.1

49092.4*b = 5108.1

Откуда b = 0.1041

Теперь найдем коэффициент «a» из уравнения (1):

10a + 2296*b = 184

10a + 2296*0.1041 = 184

10a = -54.9

a = -5.49

Получаем эмпирические коэффициенты регрессии: b = 0.1041,

a = -5.49

Уравнение регрессии (эмпирическое уравнение регрессии):

y = 0.1041 x -5.49

Параметры уравнения регрессии.
Выборочные средние.


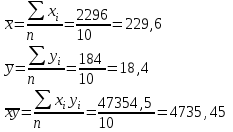
Выборочные дисперсии:




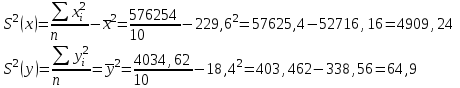
Среднеквадратическое отклонение:




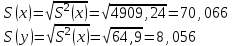
Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно:



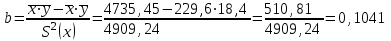
a = 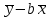 = 18.4 - 0.1041·229.6 = -5.49


Ковариация.

cov(x,y) = 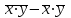 = 4735.45 - 229.6·18.4 = 510.81


Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:



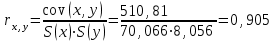
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными).

Их критерии оцениваются по шкале Чеддока:
0.1 < r_xy < 0.3: слабая;
0.3 < r_xy < 0.5: умеренная;
0.5 < r_xy < 0.7: заметная;
0.7 < r_xy < 0.9: высокая;
0.9 < r_xy < 1: весьма высокая;
Таким образом, связь между признаком Y и фактором X весьма высокая и прямая.


Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:



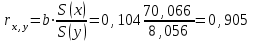
Линейное уравнение регрессии имеет вид y = 0.104 x -5.49

Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент регрессии b = 0.104 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В нашей задаче с увеличением на 1 единицу y повышается в среднем на 0.104.

---

Коэффициент a = -5.49 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

2. Задача: Определить ранговые коэффициенты корреляции по следующим статическим данным:

Банк	Собственный капитал, тыс. руб.	Активы, млн р.
А	10,8	28
Б	16,3	30
В	10,4	38
Г	14,9	33
Д	9,7	41
Е	9,0	46
Ж	7,7	44
З	6,9	49
И	5,7	52
К	5,2	50

Решение

1. 
   Коэффициент ранговой корреляции Спирмена.
   Присвоим ранги признаку Y и фактору X.
   

X	Y	ранг X, dx	ранг Y, dy
10.8	28	8	1
16.3	30	10	2
10.4	38	7	4
14.9	33	9	3
9.7	41	6	5
9	46	5	7
7.7	44	4	6
6.9	49	3	8
5.7	52	2	10
5.2	50	1	9

---

Матрица рангов.

ранг X, dx	ранг Y, dy	(dx - dy)2
8	0	64
10	0	100
7	0	49
9	0	81
6	0	36
5	0	25
4	0	16
3	0	9
2	0	4
1	0	1
55	0	385

Жирным шрифтом в таблице выделены суммы по каждому столбцу.

Проверка правильности составления матрицы на основе исчисления контрольной суммы:



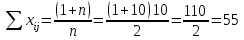
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.


По формуле вычислим коэффициент ранговой корреляции Спирмена:



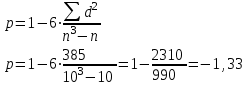
Связь между признаком Y и фактором X сильная и обратная.

2. 
   Коэффициент Кендэла.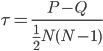
   
   

В общем случае расчет τ (точнее Р или Q) даже для N порядка 10 оказывается громоздким. Упростим.






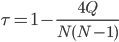
Упорядочим данные по X.
В ряду Y справа от 9 расположено 1 рангов, превосходящих 9, следовательно, 9 породит в Р слагаемое 1.
Справа от 10 стоят 0 ранга, превосходящих 10, т.е. в Р войдет 0 и т.д.

X	Y	ранг X, dx	ранг Y, dy	P	Q
5.2	50	1	9	1	8
5.7	52	2	10	0	8
6.9	49	3	8	0	7
7.7	44	4	6	1	5
9	46	5	7	0	5
9.7	41	6	5	0	4
10.4	38	7	4	0	3
10.8	28	8	1	2	0
14.9	33	9	3	0	1
16.3	30	10	2	0	0
				4	41

---

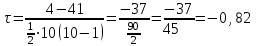
По упрощенным формулам:





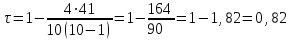
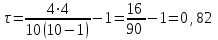
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Кендалла при конкурирующей гипотезе Н₁: τ ≠ 0. Надо вычислить критическую точку:




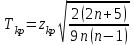
где n - объем выборки; z_kp - критическая точка двусторонней критической области, которую находят по таблице функции Лапласа по равенству Ф (z_kp)= (1 — α) /2.


Если |τ| kp — нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками незначима. Если |τ|> T_kp — нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.


Найдем критическую точку z_kp:
Ф (z_kp) = (1 - α) /2 = (1 - 0.05) /2 = 0.475


По таблице Лапласа находим z_kp = 1.96


Найдем критическую точку:



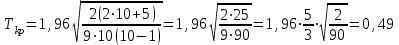
Так как τ > T_kp — отвергаем нулевую гипотезу; ранговая корреляционная связь между оценками по двум тестам значимая.

---

Смотрите также файлы

• Практическая работа Сетевое планирование.docx

• Оглавление краткая характеристика банка пао банк зенит.docx

• 20222023 оу жылы Малім Исаев Арал Айдарович.docx

• Очень слабого.odt

• Урока по литературе в 5 классе, автор учебника Тема урока Фольклор. Малые жанры фольклора..docx