ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 25
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Математическая грамотность
Комова Инна Петровна,
учитель математики МБОУ СОШ №1
Эта разработка является итогом обучения на курсах «Цифровая экосистема». В ходе занятий необходимо было выполнить практические задания по разным темам. Ситуация была предложена разработчиками курсов, а задания к ситуации нужно было составить обучающимся. В этой статье приводятся задания, разработанные мной в ходе обучения.
-
Основные понятия
Математическая грамотность—это способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира.
Контексты — это особенности и элементы окружающей обстановки, представленные в задании в рамках описанной ситуации
(личный, общественный, профессиональный и научный).
Математическое содержание разделяется на блоки:
-изменение и зависимости – задания, связанные с математическим описанием зависимости между переменными в различных процессах, т.е. с алгебраическим материалом;
-пространство и форма – задания, относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу;
-количество – задания, связанные с числами и отношениями между ними, в программах по математике этот материал чаще всего относится к курсу арифметики;
-неопределённость и данные – задания охватывают вероятностные и статистические явления и зависимости, которые являются предметом изучения разделов статистики и вероятности.
Задания по направлениям
1. Распознавание математических понятий, объектов и закономерностей в реальных жизненных ситуациях

-
Задача про гаджеты.
Трудно представить жизнь современного школьника без гаджетов, которые они используют для общения, обучения и развлечений. Однако, по мнению специалистов, гаджеты приносят школьникам не только пользу, но и вред здоровью – ухудшают зрение, портят осанку, влияют на нервную систему и др. Поэтому специалисты рекомендуют детям до 12 лет проводить за компьютером не более 1,5 часа в день.
Егору 11 лет, он учится в шестом классе и как все его сверстники очень любит гаджеты. Мама Егора решила посчитать, сколько времени он проводит с гаджетами. Один день она записывала все время, проведенное Егора с гаджетами, а затем занесла полученные данные в таблицу.
| Использование гаджета | Количество времени |
| Общение с друзьями в социальных сетях | 15.00-16.00, 21.00-21.30 |
| Подготовка к зачетной работе по математике с помощью ресурсов Интернет | 17.00-17-30 |
| Игры на телефоне | 19.00-20.00 |
| Просмотр видеороликов на различных ресурсах Интернет | 20.00-21.00 |
Задание 1.1 Соответствует ли время, которое проводит Егор с гаджетами, рекомендациям специалистов? Ответ: не соответствует
Задание 1.2 Специалисты советуют целесообразно перераспределить время использования гаджетов:
-на помощь в обучении - 25% времени;
-на общение с друзьями — 20% времени;
-на развитие навыков работы с программами-приложениями — 2/5 времени;
-на развлечения- остальное время.
Сколько времени в минутах максимально может составить просмотр Егором видеороликов на сервисе ТикТок согласно этому распределению?
Выберите один из ответов:
-
15 мин; -
13,5 мин; -
10,5 мин; -
60 мин.
Решение: 2\5 это 40%, значит на полезные дела уходит 25%+20%+40%=85%
на развлечения 15%, т. е. 90 мин х 0,15=13,5 мин. Верный ответ 2)
Задание 1.3 В 12 лет время использования гаджетов по рекомендациям специалистов может увеличиться на 2/3. Сколько минут в день сможет просматривать Егор видеоролики на сервисе ТикТок после исполнения 12 лет?
Решение: 2\3 от 90 мин это 60 минут, значит общее время составит 150 минут.
150 х 0,15 =22,5 минуты.
Задание выполнено верно, если приведены все рассуждения и дан верный ответ.

Задание 2. Проблемы загрязнения окружающей среды
20 декабря 2013 года Генеральная Ассамблея ООН провозгласила 3 марта Всемирным днем дикой природы с целью повысить уровень осведомленности широкой общественности в вопросах дикой фауны и флоры. В школе ежегодно проводятся акции в защиту животных. Учащиеся принимают участие в конкурсах плакатов и проектов, посвященных сохранению природной среды.
В школе всего учится 540 учащихся, из них – 35% учащихся начальной школы, 30% учащихся 5-6 классов и 25% учащихся 7-9 классов, остальные – учащиеся 10-11 классов.
Задание 2.1 Учащиеся старших классов вышли на уборку берега реки от различного бытового мусора. Каждый ученик 10-11 классов собрал до 10 кг мусора. Сколько контейнеров потребуется для вывоза собранного мусора, если в каждый контейнер входит до 100 кг?
Решение: 35%+30%+25%=85%, значит ученики 10-11 классов составляют 10%. 540 х 0,1= 54 ученика. 54 х 10= 540 (кг) мусора всего убрано. 540:100=5(40 остаток). Значит потребуется 6 контейнеров.
Задание выполнено верно, если приведены все рассуждения и дан верный ответ
Задание 2.2 Пятиклассники провели опрос в своей школе и выяснили, что ребята считают основными причинами, по которым животные лишаются еды и крова:
-
осушение болот — 45 % опрошенных; -
вырубку лесов — 50% опрошенных; -
охоту браконьеров -10 человек.
Можно ли утверждать, что более 210 человек из опрошенных считают основными причинами голода в животом мире экологические проблемы?Решение: 45%+50%=95%, значит 10 человек это 5%. Значит всего опрошено 10 х 20=200 человек. 210>200, и больше 190, значит это невозможно.
Задание выполнено верно, если приведены все рассуждения, обоснован выбор экологических проблем и дан верный ответ
Задание 3
На рисунке изображено 5 фигур, составленных из четырех окружностей.
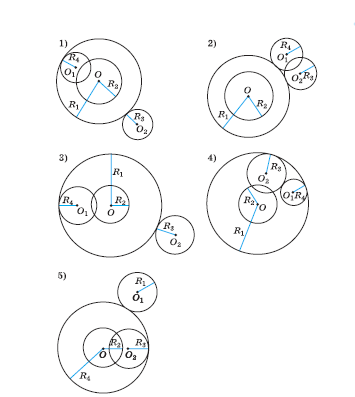
Выберите фигуру, которая удовлетворяет каждому из приведенных условий:
а) Две окружности касаются третьей ;
б) Расстояние от центра окружности О до центров окружностей О1 и О2 больше радиуса R1;
в) ОО1=ОО2;
г) окружности О1 и О2 пересекаются в двух точках;
д) Треугольник с вершинами О, О1 и О2 равнобедренный.
2. Построение математических моделей и обоснованный выбор математического аппарата для решения реальных проблем
З адание 1. Клумба
адание 1. Клумба
Для создания клумбы площадью 10 кв.м в городском парке необходимы луковицы тюльпанов и нарциссов. Плотность посадки луковичных растений на 1 кв.м следующая: тюльпаны – 15-18 шт., нарциссы – 12-15 шт.
Озеленители решили разбить клумбу, 4 4/5 площади которой занимают нарциссы, а остальную часть – тюльпаны.
1.1 Пусть площадь, занятая тюльпанами — х кв.м, а нарциссами у кв. м. Общее количество растений, удовлетворяющее условиям задания, обозначим Р. Какое наименьшее количество Р растений понадобится для озеленения клумбы?
Выберите математическую модель для решения задачи.
а) Р = 15х+12у;
б) Р = 18х+15у;
в) Р = 15х+15у;
г) Р = 18х+15у.
1.2 Дайте ответ на вопрос: какое минимальное количество растений понадобится для посадки? ________________
1.3 Изменится ли математическая модель решения задачи, если площадь, занятая тюльпанами, будет составлять 3\10 площади клумбы?
-
да; -
нет.
1.4 Дайте ответ на вопрос: какое минимальное количество растений понадобится при таком распределении площади, отведенной под нарциссы и тюльпаны?
Оценивание: верный выбор варианта ответа в заданиях 1.1 и 1.3 и верный ответ на вопрос 1.2 и 1.4.
Решение: х=10*(1/5); у=10*(4/5)
вариант а) Р=15*2+12*8=126 растений всего.
В вопросе 1.3 верный ответ 2). Формула не изменится, изменятся значения х=3 и у=7. В задании 1.4 Р=3*15+7*12=129
З
 адание 2. Помощь
адание 2. Помощь
Учащиеся школы узнали, что брату одного из учеников требуется дорогостоящая операция, и решили оказать посильную помощь в сборе средств. На Ученическом совете было принято решение собрать макулатуру и провести благотворительную ярмарку и вырученные деньги отдать в фонд помощи больному ребенку. В сборе макулатуры принимали участие ученики начальной, основной и старшей школы. Учащиеся начальной школы собрали 20% всего объема собранной макулатуры, учащиеся основной школы – 50% , остальную макулатуру собрали учащиеся старшей школы. Килограмм макулатуры можно сдать в приемный пункт по цене 18 рублей за 1 кг.
-
Какая диаграмма точнее соответствует распределению собранной макулатуры по ступеням обучения? Выберите один из вариантов ответа.
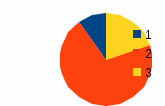
а)
б)
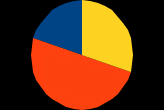
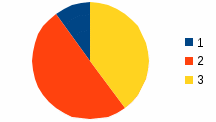
в)
-
Операция стоит 5000 рублей. Каким может быть минимальное значение А (целое количество собранной макулатуры, в кг) в формуле, дающей общую сумму, собранную школьниками, чтобы денег на оплату операции хватило:
а) А х 18 >= 5000;
б) А х 18 < =5000.
Выберите вариант, который считаете верным и запишите ответ в поле ___________.
Как изменится математическая модель, если нужно определить сумму денег, собранных учащимися старшей школы, при условии, что набрана нужная сумма.
Запишите в ответе математическую модель __________________. Вычислите эту сумму в рублях.______________
Решение: В задании 2.1 верно показано распределение на диаграмме б).
