Добавлен: 17.03.2024
Просмотров: 52
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
входят гидравлические насосные станции, которые предназначены для подачи рабочей жидкости в гидравлический инструмент. Выпускаются модели с приводом от двигателя внутреннего сгорания, с электродвигателем (220/380 В) и пневмоприводом.
Обязательно в комплект ГАСИ включается насос с ручным (ножным) приводом. Для подключения гидроинструмента к источнику питания (гидростанции или ручному насосу) и увеличения радиуса его действия используются несколько напорных и сливных рукавов, находящихся на одно- или двухбарабанных катушках или без них.
Характеристика
Для расширения возможностей ГАСИ в комплект включаются наборы цепей, специальные крюки, скобы, струбцины и упоры. В некоторые комплекты ГАСИ входят пульты дистанционного управления. В спасательных формированиях МЧС России широко используются комплекты ГАСИ «Спрут», «Медведь», «Простор», «Эконт» и др.,
Глава 2. Структурный анализ механизмов
Задача структурного анализа механизма состоит в том, чтобы определить:
Число степеней свободы плоского механизма, определяется по формуле П.Ч. Чебышева
W = 3n – 2p5 – p4
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p5 – число кинетических пар пятого класса;
p4 - число кинетических пар четвертого класса.
Степень подвижности механизма определяет число (колличество) ведущих его звеньев, которым необходимо задать движение, чтобы все остальные звенья двигались по вполне определенным законам.
Пример 1.
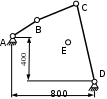
W = 3n – 2p5 – p4= 3‧5 - 2‧5 – 4 = 15 – 10 – 4 = 1
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p5 – число кинетических пар пятого класса;
p4 - число кинетических пар четвертого класса.
Пример 2
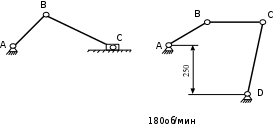
W = 3n – 2p3 – p2= 3‧3 - 2‧3 – 2 = 9 – 6 – 2 = 1
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p3 – число кинетических пар третьего класса;
p2 - число кинетических пар второго класса.
Пример 3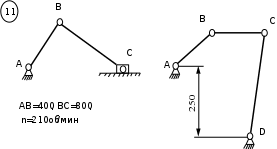
W = 3n – 2p
4 – p3= 3‧4 – 2‧4 – 3 = 12 – 8 – 3 = 1
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p4 – число кинетических пар пятого класса;
p3 – число кинетических пар четвертого класса.
2.1. Кинетический анализ механизмов
Кинематический анализ механизма – исследование его основных параметров с целью изучения законов изменения и на основе этого выбор из ряда известных наилучшего механизма. По сравнению с синтезом анализ механизма широко используется в практике.
Кинематический анализ механизма выполняется либо для заданного момента времени, либо для заданного положения входного звена; иногда для анализируемого положения механизма задают взаимное расположение каких-либо его звеньев.
Графоаналитический метод называют методом планов скоростей и ускорений.
Задача о положениях решается графическим методом, то есть построением нескольких совмещённых планов механизма в выбранном масштабе длин.
Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений звеньев механизма.
Данный метод позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма.
В основе построения планов скоростей и ускорений лежат законы плоскопараллельного движения. Согласно этим законам:
1. План скоростей (а также план ускорений) получается в результате графического решения векторных уравнений для определения скоростей (ускорений) точек в плоскопараллельном движении;
2. Векторы абсолютных скоростей точек (при рассмотрении их движения относительно неподвижного звена) изображаются исходящими из полюса плана, а направление совпадает с касательными к траектории движения. Векторы относительных скоростей точек (при их движении относительно подвижных точек) изображаются отрезками, соединяющими концы соответствующих векторов абсолютных скоростей;
3. Длина векторов относительных скоростей пропорциональна длине тех участков звеньев, которые являются радиусами вращения точек в их относительном движении. Это положение, известное под названием теоремы подобия, облегчает определение скоростей многих точек, лежащих на звеньях плоскопараллельного и вращательного движения.
Определение скоростей графоаналитическим методом
Для построения плана скоростей механизма существуют различные методы, наиболее распространённым из которых является метод векторных уравнений, разработанный советскими учёными.
Модуль скорости точки
можно определить по следующей формуле: 
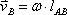. Линия действия вектора скорости точки В перпендикулярна звену АВ, а сам вектор направлен в сторону вращения звена АВ.
Допустим, что точка Е не закреплена, и представим себе, что все точки звена ВЕ совершают переносное движение со скоростью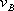
, то есть 
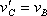. С одной стороны В1Е1=ВЕ, с другой стороны В1Е1‖ВЕ .
Вернём точку Е1 на действительную траекторию
, для чего придадим точке Е1 скорость относительного вращательного движения около точки В1 со скоростью относительного движения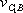 
.
На плане скоростей векторы, исходящие из полюса скоростей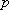
являются векторами абсолютных скоростей соответствующих точек, а векторы, которые не проходят через полюс плана ускорений, являются относительных скоростей соответствующих точек. Отрезок 
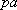является планом скоростей звена АВ, а отрезок ВЕ является планом скоростей звена ВЕ.
Пример 1
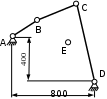
Определяем модуль vB , vC , vЕ скорости по заданым параметрам
vB= ω‧lAB= 120 ‧ 0,4 = 48 м/с
vС = ω‧lСD = 120 ‧ 0,8 = 96 м/с
vЕ = ω‧
lВЕ = 120 ‧ 0,5 = 60 м/с
где, ω – число об/мин.
LAB– длина отрезка АВ, м
lСD – длина отрезка CD, м
lВЕ – длина отрезка ВЕ, м
График 1
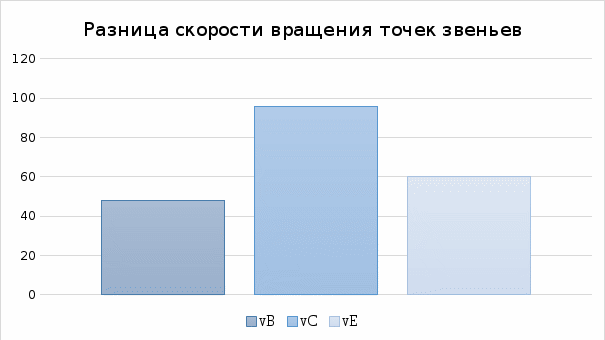
На графике наглядно показана разница модулей скорасть вращения точек звеньев плоских механизмов
Пример 2
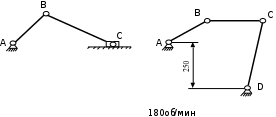
Определяем модуль vB , скорости по заданым параметрам
vB= ω‧lAB= 210 ‧ 0,4 = 84 м/с
где, ω – число об/мин.
LAB– длина отрезка АВ, м
Пример 3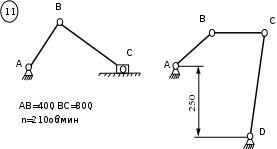
Определяем модуль vB , vC скорости по заданым параметрам
vB= ω‧lAB= 180 ‧ 0,3 = 54 м/с
vС = ω‧lСD = 180 ‧ 0,5 = 90 м/с
где, ω – число об/мин.
lAB– длина отрезка АВ, м
lСD – длина отрезка CD, м
График 2
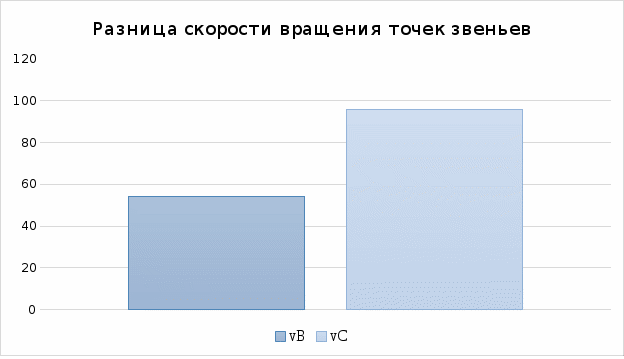
На графике наглядно показана разница модулей скорасть вращения точек звеньев плоских механизмов
2.2. Определение ускорения
Рассуждая аналогично теореме подобия для определения скоростей отдельных точек звеньев, очевидно, что план ускорений жёсткого звена подобен самому звену, и повёрнут на сто двадцать градусов.
Полное ускорение можно найти геометрически просуммировав нормальное и тангенциальное ускорения, то есть: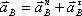
Модуль вектора нормального ускорения точки В можно найти по формуле: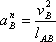
. Линия vB действия этого вектора будет перпендикулярна звену АВ.
Пример 1
Найдем ускорение aB в точке В и aС в точке С
aB =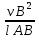
= 
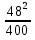
Обязательно в комплект ГАСИ включается насос с ручным (ножным) приводом. Для подключения гидроинструмента к источнику питания (гидростанции или ручному насосу) и увеличения радиуса его действия используются несколько напорных и сливных рукавов, находящихся на одно- или двухбарабанных катушках или без них.
Характеристика
| Название инструмента (показателя) | Эксплуатационные параметры инструмента | ||||
| Комплект «Простор» | Комплект «Эконт» | Комплект «Спрут» | Комплект «Медведь» | ||
| Рабочее давление | 25МПа | - | 80 МПа | - | |
| Расширители | Усилие разжима | 35 кН | 200 кН | 110 кН | - |
| Раскрытие рычагов | 320 мм | 500 мм | 845 мм | - | |
| Кусачки | Диаметр перекусываемого прутка | 25 мм | 25 мм | 32 мм | 25 мм |
| Раскрытие челюстей | До 120 мм | До 70 мм | 135 мм | До 70 мм | |
| Комбинированные ножницы | Толщина разрезаемой пластины | 4 мм | До 10 мм | До 10 мм | 10 мм |
| Раскрытие челюстей | 420 мм | До 160 мм | 335 мм | 240 мм | |
| Гидравлические цилиндры | Усилие подъема/стягивания | 120/60 кН | 230/130 кН | 140/55 кН | 220/130 кН |
| Ход штока | До 640 мм | До 400 мм | До 540 мм | 400 мм | |
| Вспомогательные инструменты (назначение) | нет | кусачки для перекусывания арматуры и гаек болтовых соединений, резак тросовый, резак для кабелей | отрыватель петель, тросорез, скоба-кусачки | кусачки для перекусывания арматуры и гаек болтовых соединений | |
| Инструменты со встроенным насосом (назначение) | нет | кусачки для перекусывания круглых металлических кабелей | Расширитель дверной | нет | |
| Насосные санции | Тип приводного двигателя | 2-тактный ДВС, эл. дв. 220 В, эл. дв. 380 В | 2-тактный ДВС, эл. дв. 220 В пневмопривод | ДВС | 4-тактный ДВС, эл. дв. 220 В, эл. дв. 380 В |
| Масса станции | с ДВС – 20 кг, с эл. дв. – 31 кг | - | До 18 кг | До 24 кг | |
Для расширения возможностей ГАСИ в комплект включаются наборы цепей, специальные крюки, скобы, струбцины и упоры. В некоторые комплекты ГАСИ входят пульты дистанционного управления. В спасательных формированиях МЧС России широко используются комплекты ГАСИ «Спрут», «Медведь», «Простор», «Эконт» и др.,
Глава 2. Структурный анализ механизмов
Задача структурного анализа механизма состоит в том, чтобы определить:
-
Число степеней свободы механизма или число ведущих звеньев механизма; -
Число структурных групп Ассура, входящих в состав механизма, их класс, порядок и вид.
Число степеней свободы плоского механизма, определяется по формуле П.Ч. Чебышева
W = 3n – 2p5 – p4
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p5 – число кинетических пар пятого класса;
p4 - число кинетических пар четвертого класса.
Степень подвижности механизма определяет число (колличество) ведущих его звеньев, которым необходимо задать движение, чтобы все остальные звенья двигались по вполне определенным законам.
Пример 1.
W = 3n – 2p5 – p4= 3‧5 - 2‧5 – 4 = 15 – 10 – 4 = 1
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p5 – число кинетических пар пятого класса;
p4 - число кинетических пар четвертого класса.
Пример 2
W = 3n – 2p3 – p2= 3‧3 - 2‧3 – 2 = 9 – 6 – 2 = 1
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p3 – число кинетических пар третьего класса;
p2 - число кинетических пар второго класса.
Пример 3
W = 3n – 2p
4 – p3= 3‧4 – 2‧4 – 3 = 12 – 8 – 3 = 1
Где W– ступень подвижности механизма;
n – число подвижных звеньев механизма;
p4 – число кинетических пар пятого класса;
p3 – число кинетических пар четвертого класса.
2.1. Кинетический анализ механизмов
Кинематический анализ механизма – исследование его основных параметров с целью изучения законов изменения и на основе этого выбор из ряда известных наилучшего механизма. По сравнению с синтезом анализ механизма широко используется в практике.
Кинематический анализ механизма выполняется либо для заданного момента времени, либо для заданного положения входного звена; иногда для анализируемого положения механизма задают взаимное расположение каких-либо его звеньев.
Графоаналитический метод называют методом планов скоростей и ускорений.
Задача о положениях решается графическим методом, то есть построением нескольких совмещённых планов механизма в выбранном масштабе длин.
Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений звеньев механизма.
Данный метод позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма.
В основе построения планов скоростей и ускорений лежат законы плоскопараллельного движения. Согласно этим законам:
1. План скоростей (а также план ускорений) получается в результате графического решения векторных уравнений для определения скоростей (ускорений) точек в плоскопараллельном движении;
2. Векторы абсолютных скоростей точек (при рассмотрении их движения относительно неподвижного звена) изображаются исходящими из полюса плана, а направление совпадает с касательными к траектории движения. Векторы относительных скоростей точек (при их движении относительно подвижных точек) изображаются отрезками, соединяющими концы соответствующих векторов абсолютных скоростей;
3. Длина векторов относительных скоростей пропорциональна длине тех участков звеньев, которые являются радиусами вращения точек в их относительном движении. Это положение, известное под названием теоремы подобия, облегчает определение скоростей многих точек, лежащих на звеньях плоскопараллельного и вращательного движения.
Определение скоростей графоаналитическим методом
Для построения плана скоростей механизма существуют различные методы, наиболее распространённым из которых является метод векторных уравнений, разработанный советскими учёными.
Модуль скорости точки
можно определить по следующей формуле: . Линия действия вектора скорости точки В перпендикулярна звену АВ, а сам вектор направлен в сторону вращения звена АВ.Допустим, что точка Е не закреплена, и представим себе, что все точки звена ВЕ совершают переносное движение со скоростью
, то есть . С одной стороны В1Е1=ВЕ, с другой стороны В1Е1‖ВЕ .Вернём точку Е1 на действительную траекторию
, для чего придадим точке Е1 скорость относительного вращательного движения около точки В1 со скоростью относительного движения .На плане скоростей векторы, исходящие из полюса скоростей
являются векторами абсолютных скоростей соответствующих точек, а векторы, которые не проходят через полюс плана ускорений, являются относительных скоростей соответствующих точек. Отрезок является планом скоростей звена АВ, а отрезок ВЕ является планом скоростей звена ВЕ.Пример 1
Определяем модуль vB , vC , vЕ скорости по заданым параметрам
vB= ω‧lAB= 120 ‧ 0,4 = 48 м/с
vС = ω‧lСD = 120 ‧ 0,8 = 96 м/с
vЕ = ω‧
lВЕ = 120 ‧ 0,5 = 60 м/с
где, ω – число об/мин.
LAB– длина отрезка АВ, м
lСD – длина отрезка CD, м
lВЕ – длина отрезка ВЕ, м
График 1
На графике наглядно показана разница модулей скорасть вращения точек звеньев плоских механизмов
Пример 2
Определяем модуль vB , скорости по заданым параметрам
vB= ω‧lAB= 210 ‧ 0,4 = 84 м/с
где, ω – число об/мин.
LAB– длина отрезка АВ, м
Пример 3
Определяем модуль vB , vC скорости по заданым параметрам
vB= ω‧lAB= 180 ‧ 0,3 = 54 м/с
vС = ω‧lСD = 180 ‧ 0,5 = 90 м/с
где, ω – число об/мин.
lAB– длина отрезка АВ, м
lСD – длина отрезка CD, м
График 2
На графике наглядно показана разница модулей скорасть вращения точек звеньев плоских механизмов
2.2. Определение ускорения
Рассуждая аналогично теореме подобия для определения скоростей отдельных точек звеньев, очевидно, что план ускорений жёсткого звена подобен самому звену, и повёрнут на сто двадцать градусов.
Полное ускорение можно найти геометрически просуммировав нормальное и тангенциальное ускорения, то есть:
Модуль вектора нормального ускорения точки В можно найти по формуле:
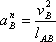. Линия vB действия этого вектора будет перпендикулярна звену АВ.Пример 1
Найдем ускорение aB в точке В и aС в точке С
aB =
=