ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Производная степенной функции
Прологарифмируем левую и правую части равенства с основой e.
Дифференцируя обе части равенства, получим:
Учитывая, что у является функцией х и использовав правило дифференцирования составной функции будем иметь:
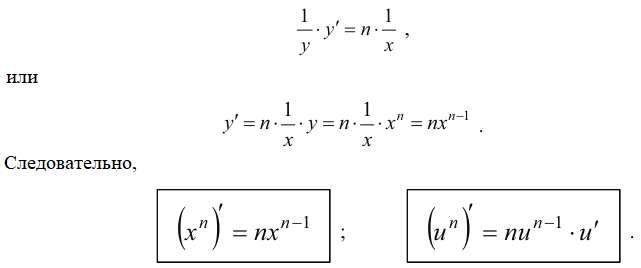
Производная показательной функции
Прологарифмируем левую и правую части равенства.

Производная показательно-степной функции
Это показательно-степенная функция, поскольку и основание, и показатель степени содержат переменную x.
Действуем по схеме: сначала логарифмируем обе части по основанию e:
Показатель степени выносим за знак логарифма:
Теперь дифференцируем обе части равенства, с учетом того, что y=y(x), а значит, lny — сложная функция:
Обе части равенства умножаем на y:
Вспоминаем, что по условию y — это x в степени sinx, и подставляем это выражение вместо y:
Действуем по схеме:
Здесь ln(2x+3) — сложная функция, внешняя функция f=lnu. внутренняя u=2x+3:
Умножаем обе части равенства на y:
Теперь подставляем в вместо y его выражение из условия:
Логарифмируем обе части по основанию e:
Показатель степени выносим за знак логарифма:
Теперь дифференцируем обе части равенства:
√(7-x) сложная функция, внешняя функция f=√u, внутренняя u=7-x:
Теперь обе части умножаем на y:
И в завершении, заменяем y на соответствующее выражение из условия:
