Файл: Геометрические Приложения криволинейных интегралов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 12
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Окрестностью поверхности 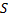 будем называть любое открытое множество
будем называть любое открытое множество  , содержащее
, содержащее 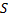 .
.
Т2.
Пусть в некоторой окрестности поверхности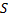 ф.
ф.  ,
, 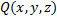 ,
, 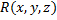 непрерывны и имеют непрерывные частные производные первого порядка. Если
непрерывны и имеют непрерывные частные производные первого порядка. Если  несобственные интегралы по области
несобственные интегралы по области 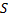 от каждой из частных производных ф.
от каждой из частных производных ф.  ,
, 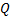 и
и 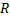 , то справедливо соотношение:
, то справедливо соотношение:

называемое формулой Стокса. При этом стоящий в правой части интеграл представляет собой сумму интегралов по связным компонентам границы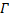 , на которых указано такое направление обхода, при котором область
, на которых указано такое направление обхода, при котором область 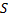 остаётся слева.
остаётся слева.
Формула Остроградского.
Формула связывает тройной интеграл с поверхностным интегралом на границе области.
Пусть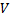
– конечная, многосвязная область в пространстве с кусочно-гладкой границей
с кусочно-гладкой границей 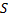 . Область
. Область  с присоединённой границей будем обозначать через
с присоединённой границей будем обозначать через 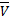 .
.
Т3.
Пусть ф. ,
,  ,
,  непрерывны в
непрерывны в 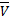 и имеют непрерывные частные производные первого порядка в
и имеют непрерывные частные производные первого порядка в  . Если
. Если  несобственные интегралы по области
несобственные интегралы по области 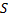 от каждой из частных производных ф.
от каждой из частных производных ф.  ,
, 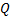 и
и  , то справедливо соотношение:
, то справедливо соотношение:
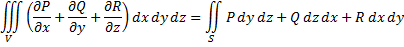
называемое формулой Остроградского. При этом стоящий в правой части интеграл представляет собой сумму интегралов по связным компонентам границы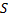 , на которых выбрана внешняя по отношению к
, на которых выбрана внешняя по отношению к  сторона.
сторона.
Т2.
Пусть в некоторой окрестности поверхности
называемое формулой Стокса. При этом стоящий в правой части интеграл представляет собой сумму интегралов по связным компонентам границы
Формула Остроградского.
Формула связывает тройной интеграл с поверхностным интегралом на границе области.
Пусть
– конечная, многосвязная область в пространстве
Т3.
Пусть ф.
называемое формулой Остроградского. При этом стоящий в правой части интеграл представляет собой сумму интегралов по связным компонентам границы

