Файл: Отчет по практической работе 1 Парный регрессионный анализ построение модели в виде парной регрессии и проверка ее качества по дисциплине Эконометрика.docx

Федеральное государственное автономное

образовательное учреждение

высшего образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт управления бизнес- процессами и экономики

Кафедра «Экономика и управление бизнес-процессами»

ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ №1

Парный регрессионный анализ: построение модели в виде парной регрессии и проверка ее качества по дисциплине «Эконометрика»

Вариант №1

Преподаватель __________ Л.В. Гаврилова

подпись, дата инициалы, фамилия
Студент УБ20-15 __________ Д.Н. Абалакова

номер группы подпись, дата инициалы, фамилия

Красноярск 2021

СОДЕРЖАНИЕ

Задание:

Исходные данные: наблюдаемые значения переменных x и y заданы в таблице 1:

1. 
   Построить линейную и нелинейные (в соответствии с вариантом) модели регрессии.
   
2. 
   Вычислить показатели качества и точности для каждого уравнения;
   
3. 
   Проверить значимость уравнений регрессии при уровнях значимости 0,05 и 0,01;
   
4. 
   Определить средние коэффициенты эластичности по построенным уравнениям регрессии;
   
5. 
   Определить лучшее уравнение регрессии на основе средней ошибки аппроксимации и коэффициента детерминации.;
   
6. 
   Для линейной регрессии проверить значимость полученных коэффициентов и построить доверительные интервалы для точных значений параметров a и b. Уровни значимости 0,05 и 0,01;
   
7. 
   Выполнить точечный и интервальный прогноз в предположении роста значения факторного признака на 15% от среднего уровня по лучшему уравнению регрессии. Прогноз дать с уровнем доверия 95% и 99%;
   
8. 
   Графически представить результаты моделирования.
   

Ход работы:

Таблица 1 – Исходные данные

№ наблюдения	x	y	№ наблюдения	x	y
1	0,16	21,1	24	0,79	20,9
2	0,8	20,6	25	0,22	21,2
3	0,94	20,7	26	0,39	21
4	0,26	22,1	27	0,57	19,5
5	0,27	20,2	28	0,24	20,8
6	0,47	19,8	29	0,08	21,6
7	0,34	21,3	30	0,53	19,9
8	0,31	20,2	31	0,24	21,2
9	0,65	20	32	0,12	22
10	0,06	21,4	33	0,76	20,6
11	0,14	20,7	34	0,61	20,2
12	0,1	20,9	35	0,85	20,5
13	0,81	20,3	36	0,39	21,9
14	0,19	21,6	37	0,23	21,2
15	0,39	20,1	38	0,77	20,1
16	0,91	19,6	39	0,29	22,1
17	0,64	20,3	40	0,99	19,6
18	0,87	18,5	41	0,83	20
19	0,33	20,9	42	0,44	21,5
20	0,92	19,5	43	0,03	22,2
21	0,49	20,1	44	0,07	21,8
22	0,17	20	45	0,75	20,1
23	0,47	20,1

---

1. 
   Для построения уравнения линейной регрессии используем инструмент «Регрессия'>Данные/Анализ данных/Регрессия» (рисунок 1).
   

Рисунок 1 – Окно параметров регрессии

Задав соответствующие диапазоны данных в окне, получим набор таблиц Л.А, Л.Б, Л.В.

Таблица Л.А – Регрессионная статистика

Множественный R	0,666301
R-квадрат	0,443957
Нормированный R-квадрат	0,431026
Стандартная ошибка	0,629897
Наблюдения	45

Таблица Л.Б – Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия	1	13,62198	13,62198	34,33212	5,85E-07
Остаток	43	17,06113	0,396771
Итого	44	30,68311

Таблица Л.В – Коэффициенты регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 99,0%	Верхние 99,0%
Y-пересечение	21,552	0,178	120,955	0,000	21,192	21,911	21,192	21,911
х	-1,912	0,326	-5,859	0,000	-2,570	-1,254	-2,570	-1,254

---

Из таблицы Л.В следует, что уравнение регрессии имеет вид



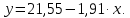
Для построения полинома второй степени 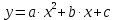введем две замены 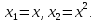В результате приходим к двухфакторному уравнению:

.

Это линейное уравнение, параметры которого можно определить с помощью инструмента Регрессия из пакета Анализ данных.

Вычислим значения новых переменных (таблица 2)

Таблица 2 – Значения новых переменных для регрессии полинома 2 степени

№ наблюдения	x2	x1	y	№ наблюдения	x2	x1	y
1	0,0256	0,16	21,1	24	0,6241	0,79	20,9
2	0,64	0,8	20,6	25	0,0484	0,22	21,2
3	0,8836	0,94	20,7	26	0,1521	0,39	21
4	0,0676	0,26	22,1	27	0,3249	0,57	19,5
5	0,0729	0,27	20,2	28	0,0576	0,24	20,8
6	0,2209	0,47	19,8	29	0,0064	0,08	21,6
7	0,1156	0,34	21,3	30	0,2809	0,53	19,9
8	0,0961	0,31	20,2	31	0,0576	0,24	21,2
9	0,4225	0,65	20	32	0,0144	0,12	22
10	0,0036	0,06	21,4	33	0,5776	0,76	20,6
11	0,0196	0,14	20,7	34	0,3721	0,61	20,2
12	0,01	0,1	20,9	35	0,7225	0,85	20,5
13	0,6561	0,81	20,3	36	0,1521	0,39	21,9
14	0,0361	0,19	21,6	37	0,0529	0,23	21,2
15	0,1521	0,39	20,1	38	0,5929	0,77	20,1
16	0,8281	0,91	19,6	39	0,0841	0,29	22,1
17	0,4096	0,64	20,3	40	0,9801	0,99	19,6
18	0,7569	0,87	18,5	41	0,6889	0,83	20
19	0,1089	0,33	20,9	42	0,1936	0,44	21,5
20	0,8464	0,92	19,5	43	0,0009	0,03	22,2
21	0,2401	0,49	20,1	44	0,0049	0,07	21,8
22	0,0289	0,17	20	45	0,5625	0,75	20,1
23	0,2209	0,47	20,1

---

Для построения линеаризованного уравнения регрессии полинома второй степени используем инструмент «Данные/Анализ данных/Регрессия», в качестве Входного интервала Х указываем диапазон со значениями x₁, x₂, а для Входного интервала У указываем диапазон со значениями y. В результате получим три таблицы:

Таблица ПОЛ.А – Регрессионная статистика

Множественный R	0,676065
R-квадрат	0,457063
Нормированный R-квадрат	0,431209
Стандартная ошибка	0,629796
Наблюдения	45

Таблица ПОЛ.Б – Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия	2	14,02412	7,012062	17,67854	2,69E-06
Остаток	42	16,65899	0,396643
Итого	44	30,68311

Таблица ПОЛ.В – Коэффициенты регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	21,787	0,294	74,149	0,000	21,194	22,380	21,194	22,380
x2	1,409	1,400	1,007	0,320	-1,415	4,234	-1,415	4,234
x1	-3,325	1,440	-2,308	0,026	-6,231	-0,418	-6,231	-0,418

---

По таблице ПОЛ.В определяем параметры a=1,409; b=-3,325; c=21,787.

Таким образом, уравнение регрессии полинома второй степени имеет вид:

.
Для построения степенной модели 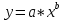проведем линеаризацию:

.

Введем новые переменные x'= lnx; y'= lny и новый параметр а₀ = lna, тогда в новых переменных уравнение будет иметь следующий вид:



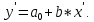
Это линейное уравнение, параметры которого можно определить с помощью инструмента Регрессия из пакета Анализ данных.

Вычислим значения новых переменных (таблица 3).

Таблица 3 – Значения новых переменных для степенной регрессии

№ наблюдения	x'=lnx	y'=lny	№ наблюдения	x'=lnx	y'=lny
1	-1,833	3,049	24	-0,236	3,040
2	-0,223	3,025	25	-1,514	3,054
3	-0,062	3,030	26	-0,942	3,045
4	-1,347	3,096	27	-0,562	2,970
5	-1,309	3,006	28	-1,427	3,035

Продолжение таблицы 3

№ наблюдения	x'=lnx	y'=lny	№ наблюдения	x'=lnx	y'=lny
6	-0,755	2,986	29	-2,526	3,073
7	-1,079	3,059	30	-0,635	2,991
8	-1,171	3,006	31	-1,427	3,054
9	-0,431	2,996	32	-2,120	3,091
10	-2,813	3,063	33	-0,274	3,025
11	-1,966	3,030	34	-0,494	3,006
12	-2,303	3,040	35	-0,163	3,020
13	-0,211	3,011	36	-0,942	3,086
14	-1,661	3,073	37	-1,470	3,054
15	-0,942	3,001	38	-0,261	3,001
16	-0,094	2,976	39	-1,238	3,096
17	-0,446	3,011	40	-0,010	2,976
18	-0,139	2,918	41	-0,186	2,996
19	-1,109	3,040	42	-0,821	3,068
20	-0,083	2,970	43	-3,507	3,100
21	-0,713	3,001	44	-2,659	3,082
22	-1,772	2,996	45	-0,288	3,001
23	-0,755	3,001

---