Файл: Отчет по практической работе 1 Парный регрессионный анализ построение модели в виде парной регрессии и проверка ее качества по дисциплине Эконометрика.docx

Для построения линеаризованного уравнения степенной регрессии используем инструмент «Данные/Анализ данных/Регрессия», в качестве Входного интервала Х и Входного интервала У указываем диапазоны со значениями x' и y'. В результате получим три таблицы:

Таблица С.А – Регрессионная статистика

Множественный R	0,663271
R-квадрат	0,439929
Нормированный R-квадрат	0,426904
Стандартная ошибка	0,030651
Наблюдения	45

Таблица С.Б – Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия	1	0,031732	0,031732	33,77591	6,87E-07
Остаток	43	0,040398	0,000939
Итого	44	0,07213

Таблица С.В – Коэффициенты регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	2,9947	0,0073	411,4614	0,0000	2,9800	3,0094
x'=ln(x)	-0,0316	0,0054	-5,8117	0,0000	-0,0425	-0,0206

---

По таблице С.В определяем параметры а₀=lna=2,9947 и ????=-0,031.

Найдем параметр a:



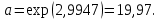
Таким образом, уравнение степенной регрессии имеет следующий вид:


2) Вычисление показателей качества: линейного коэффициента парной корреляции 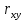(индекса корреляции R), коэффициента (индекса) детерминации , средней ошибки аппроксимации ????̅ .

Для линейной модели значение коэффициента корреляции 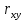получим по функции КОРРЕЛ, коэффициент детерминации возьмём из таблицы с регрессионной статистикой для линейной модели (таблица Л.А): 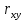= 0,6663, = 0,4440.

Для определения средней ошибки аппроксимации выполним промежуточные расчеты для линейной модели (таблица 8).

Таблица 8 – Промежуточные результаты расчетов для линейной регрессии

Номер наблюдения	x	y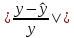
1	0,16	21,1	21,2444	0,006844
2	0,8	20,6	20,022	0,028058
…	…	…	…	…
45	0,75	20,1	20,1175	0,000871
Сумма	20,88	929,9	929,8692	1,075024
Среднее значение	0,464	20,66444	20,66376	0,023889

---

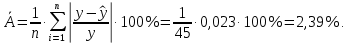
Для нелинейных моделей значения индекса корреляции и индекса детерминации можем взять из вспомогательных таблиц с регрессионной статистикой («R-квадрат» и «Множественный R»), а также вручную с помощью следующих формул:

,

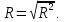
Для степенной модели значение построим вспомогательную таблицу (таблица 9).

Таблица 9 – Промежуточные результаты расчетов для степенной регрессии

Номер наблюдения	x'=ln(x)	y'=ln(y)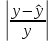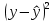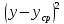
1	-1,833	3,049	21,1469	0,0022	0,0022	0,1897
2	-0,223	3,025	20,1177	0,0234	0,2326	0,0042
…	…	…	…	…	…	…
45	-0,288	3,001	20,1580	0,0029	0,0034	0,3186
Сумма	-46,9185	136,2426	928,9067	1,0648	17,14834	30,68311

Тогда



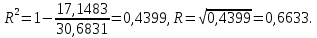
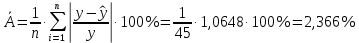
Для модели полинома второй степени значение построим вспомогательную таблицу (таблица 14)

Таблица 14 – Промежуточные результаты расчетов для полинома второй степени

Номер наблюдения	x'=x2	x	y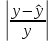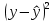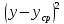
1	0,0256	0,16	21,1	21,2949	0,009237	0,037984	0,189709
2	0,64	0,8	20,6	20,0364	0,027359	0,317645	0,004153
…	…	…	…	…	…	…	…
45	0,5625	0,75	20,1	20,09313	0,000342	4,73E-05	0,318598
Сумма	13,4136	20,88	929,9	930,1416	1,06276	16,66039	30,68311

---

Тогда





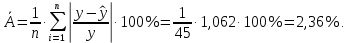
3) Проверка значимости уравнений регрессии (п.3).

Для линейной модели ????_факт определяем по таблице дисперсионного анализа (таблица Л.Б).

F_факт= 34,33.





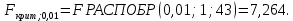
Следовательно, при α = 0,05 линейное уравнение значимо, при α = 0,01 также значимо.

Для степенной модели:



F_{крит;0,05} и F_{крит;0,01} – те же самые. При α = 0,05 степенное уравнение значимо, при α = 0,01 также значимо.

Для полинома второй степени:



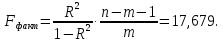
F_{крит;0,05}=3,22

F_{крит;0,01}=5,15

При α = 0,05 степенное уравнение значимо, при α = 0,01 также значимо.

4) Определение среднего коэффициента эластичности по уравнению линейной регрессии:



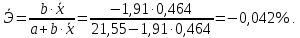
Для степенной модели:



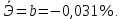
Для полинома 2 степени:



5) Определение лучшего уравнения регрессии (по средней ошибке аппроксимации)

Полином второй степени даёт меньшую погрешность, так как _лог. = 2,36%, что является наименьшим значением погрешности среди исследуемых функций. Коэффициент детерминации для полинома чуть выше остальных анализируемых моделей (логарифмическое уравнение объясняет  45 % вариации результативного признака), поэтому логарифмическая модель чуть лучше, чем остальные модели. Тем не менее, значение коэффициента детерминации невелико, поэтому эти модели нельзя считать пригодными для прогноза.

6) Проверка значимости коэффициентов линейной регрессии. Значимость параметров линейной регрессии определяем по таблице Л.В. (столбец P-значение). Значимость t-критерия для параметра а уравнения регрессии меньше заданного уровня значимости, следовательно, этот параметр значим. Значимость параметра

---

b меньше заданного уровня значимости, следовательно, b значим.

6) Определение доверительных интервалов для точных значений параметров a и b уравнения линейной регрессии.

Для точного значения параметра a доверительный интервал при уровне значимости 5% находим по таблице Л.В., столбцы Нижние 95%, Верхние 95%:



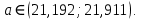
При уровне значимости 1% находим по таблице Л.В., столбцы Нижние 99%, Верхние 99%:



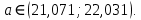
Доверительный интервал для точного значения параметра b при уровне значимости 5% находим по таблице Л.В., столбцы Нижние 95%, Верхние 95%:



При уровне значимости 1% находим по таблице Л.В., столбцы Нижние 99%, Верхние 99%:



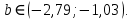
7) Построение точечного и интервального прогноза для значения

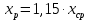по лучшему уравнению регрессии.

Лучшая модель – полином второй степени. Выполним точечный и интервальный прогноз по уравнению регрессии логарифмической модели.

Точечный прогноз :



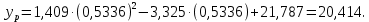
Выполним интервальный прогноз — для 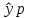и построим доверительный интервал с вероятностью P = 95%. Для этого вычислим:



Интервальный прогноз:

Выполним интервальный прогноз — для 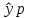и построим доверительный интервал с вероятностью P = 99%. Для этого вычислим:



Интервальный прогноз:

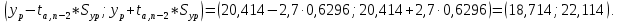
Результаты:

1. 
   Уравнения регрессии:
   

Уравнение линейной регрессии:

Уравнение полинома 2 степени:

Уравнение степенной регрессии:

---