ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.03.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ақтөбе облысы, Шалқар ауданы
№6 орта мектебі
Мұғалімі: Шаймерденова Ақалтын Айдуллақызы
Сыныбы: 9ә
Пәні: геометрия
Сабақтың тақырыбы: Косинустар теоремасы
Сабақтың түрі: аралас (І кезең – 5 минут; ІІ кезең – 25 минут; Ш кезең – 15 минут)
1. Сабақтың мақсаты:
- білімділік Косинустар теоремасын есте сақтау. Үшбұрыштарды шешуде косинустар теоремасын қолдана білудің жалпы тәсілімен оқушыларды таныстыру.
- тәрбиелік: жеке жұмыс жасауға, жауапкершілікті сезіне білуге, нәтижеге жетуге ұмтылуға, өзінше ізденімпаздыққа, еңбек етуге ,әр жеке тұлғаның шығармашылық қабілеттерін ұштау,жеке қабілеті мен белсенділігін дамыта отырып, шығармашылыққа баулу, алған білімдерін күнделікті өмірде пайдалана білуге дағдыландыру, оларды күнделікті өмірде қолдануға бағытталған тапсырмалар беру арқылы тәрбиелеу;
-дамытушылық: әр оқушының үш деңгейлік тапсырмаларды біртіндеп орындауына жағдай жасау арқылы оның қабілетіне сәйкес жеке құзырлылығын дамыту.
2. Сабақтың мазмұны:
І –Ш кезеңдік тапсырмалар (төменде оқушының жұмыс дәптерінде және мұғалімге арналған жауаптар-кілтінде берілген)
3. Сабақтың әдіс-тәсілдері:
І кезеңде – сұрақ- жауап;
ІІ кезеңде – а) оқулықпен өз бетімен іздену әдісі;
б) практикада бекіту әдісі.
Ш кезеңде –үшдеңгейлік тапсырмаларды өз бетімен біртіндеп орындату арқылы бағалау әдістері.
4. көрнекіліктері:
І кезеңде – жұмыс дәптері, тақтадағы «ашық журнал», мұғалім мен оқушылардың жеке журналдары
ІІ кезеңде – а) оқулық; слайдтар
б) оқулық, жұмыс дәптері;
в) оқулық, жұмыс дәптері, тақта, бор
Ш кезеңде – жұмыс дәптері, тақтадағы «ашық журнал», мұғалім мен оқушылардың жеке журналдары
Сабақтың өту барысы:
І кезеңде – а) ұйымдастыру; б) үй тапсырмасын тексеріп тақтадағы ашық журналға белгілеу;
в) «көпір тапсырмаларын» тексеру.
ІІ кезеңде–а) оқушылардың топта өз бетімен жұмыс дәптерінде берілген жетелеуші тапсырмаларға оқулықтан жауап іздеуі. Мұғалімнің тақтадағы «ашық журналдағы» алдында өткен тақырып бойынша жиналған жалпы ұпай санын өзінің жеке журналына және сынып журналына баға түрінде тіркеуі.
б) мұғалімнің көмегімен дискуссия жүргізу;
в) тақтамен, оқулықпен жеке жұмыс.
Ш кезеңде – дұрыс орындалған деңгейлік тапсырмаларды мұғалімнің тексеруінен кейін оқушылардың өзіне тақтадағы «ашық журналға» белгілетіп отыру, жиған алғашқы ұпайларын қорыту, оларды оқушылардың жеке журналдарына тіркету және қалған тапсырмаларды үйде аяқтап келуге беру. Үш деңгейді толық орындаған оқушыға төртінші деңгейдің олимпиадалық немесе ғылыми жобадан фрагмент тапсырмаларын беру. Қосымша, келесі тақырыптың бірінші кезеңіндегі «көпір тапсырмаларын» орындап келуге беру.
Сабақтың тақырыбы: Косинустар теоремасы
Мұғалімге арналған кілті
| «Көпір» тапсыр-малары | I кезең 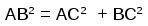 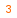 |
| «Білу» тапсыр-малары Кім? Не? Қалай? Қашан? Қандай? | II кезең Бос орынға қажет сөзді жаз: Косинустар теоремасы – үшбұрыштың екі қабырғасы мен сол екі қабырғаның арасындағы бұрышы бойынша оның үшінші қабырғасын анықтауға арналған теорема. Бұл теорема былайша тұжырымдалады: кез келген үшбұрыштың бір қабырғасының квадраты қалған екі қабырғасының квадраттарының қосындысынан олардың ұзындықтары мен арасындағы бұрыштың косинусының екі еселенген көбейтіндісін шегергенге тең: с2=а2+b2-2аb 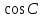 мұндағы a, b, c – үшбұрыштың қабырғалары, Д   әлелдеуі : Үшбұрыш ABC-ны қарастырайық. А әлелдеуі : Үшбұрыш ABC-ны қарастырайық. АДәлелдеу керек: |АВ|2=|АС|2+|ВС|2-2 |АС||ВС| 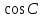 , с b , с bя  ғни с2=а2+b2-2аb ғни с2=а2+b2-2аb 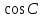 Векторларды қосу ережесі бойынша : В а С 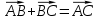 , бұдан , бұдан 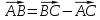 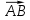 векторын өзіне – өзін скалярлық көбейтейік: векторын өзіне – өзін скалярлық көбейтейік: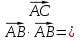 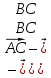 = =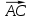 2+ 2+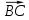 2-2 2-2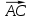 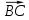 = =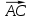 2 + 2 +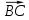 2 -2 2 -2 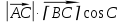 , яғни АВ2=АС2+ВС2-2 АСВС , яғни АВ2=АС2+ВС2-2 АСВС 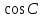 немесе с2=а2+b2-2аb немесе с2=а2+b2-2аb 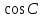 Теорема дәлелденді Ескерту. Косинустар теоремасы Пифагор теоремасының жалпыламасы болады, өйткені γ=900 десек онда cos γ=cos 900 =0 және c2=a2+b2-2ab cos γ=c2=a2+b2 болады. C төбесінен AB қабырғасына CD биіктік түсірейік. ADC үшбұрышынан: 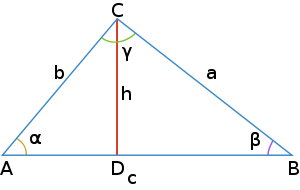 Пифагор теоремасын екі тік бұрышты үшбұрыш ADC мен BDC үшін жазайық: (1) мен (2) теңдеулерінің оң жақтарын теңестірсек: немесе Кез келген үшбұрыш үшін мына формулалар орынды: c2=a2+b2-2ab cos γ b2=a2+c2-2ac cos β a2=b2+c2-2bc cos α |
| «Түсіну» тапсырмалары Неліктен? Неге? Не үшін? Не себепті? | Бос орынға қажет сөзді жаз. Берілген екі қабырғасының арасындағы бұрыш тік болған жағдайда косинустар теоремасы тура бола ма? Себебі: Косинустар теоремасы Пифагор теоремасының жалпыламасы болады, өйткені γ=900 десек онда cos γ=cos 900 =0 және c2=a2+b2-2ab cos γ=c2=a2+b2 болады. |
| «Талдау» тапсыр-малары | Венн диаграммасы Пифогор теоремасы Ортақ Косинустар теоремасының  |
| «Жинақ-тау» тапсыр-масы |
3 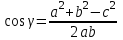 . .b2=a2+c2-2ac cos β 4 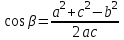 . .5 a2=b2+c2-2bc cos α . 6. |
| «Қолда-ну» тапсыр-малары | Оқулықтан төмендегі тапсырмаларды орында : № 272 АВС үшбұрышында АВ═4 см, , ∟С═30°,∟В═45°. АС қабырғасының ұзындығын табыңдар |
| «Баға беру» | Сен қалай ойлайсың? Косинустар теоремасын күнделікті өмірде қолдануға бола ма? |
| «Кері байланыс» Теория: «Білу» Практика | III кезең
1. KHT үшбұрышы берілген. Көп нүктенің орнын толықтыр а) KH; б) HT; в) TK. 2. DEF үшбұрышы берілген. Тура теңдікті табыңдар: а) 3. ESR үшбұрышы берілген. Көп нүктенің орнын толықтыр а) SE; б) SR; в) ER. 4. Тура теңдікті табыңдар: а) 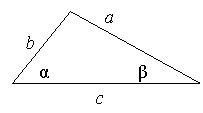 ) ) 5. №267 Үшбұрыштың қабырғалары : 13 м , 14 м, 15 м. А бұрышының косинусын табыңдар? |
| Теория: «Түсіну» Неліктен? Неге? Не үшін? Не себепті? Практика | 2-деңгей (5+4 балл) «4»
Топтастыру стратегиясы 
№ 273 АВС үшбұрышында АВ═10 см, , ∟С═60°,∟В═45°. АС қабырғасының ұзындығын табыңдар № 275 АВС үшбұрышында ВС═6 см, ∟А═60°, ∟В═45°. АС қабырғасының ұзындығын табыңдар |
| «Жинақтау» , «Талдау» Практика |
Үшбұрыштың белгісіз қабырғасын табыңдар 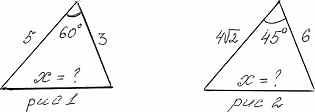 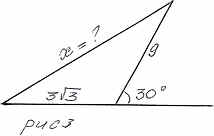 Жауаптары: 1) х = 2) х = 3) х =
АВС үшбұрышында ∟А═45°,∟С═30°. АД биіктігі 30 см . Үшбұрыш қабырғаларының ұзындығын табыңдар |
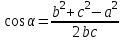 ауаптарын сәйкестендір:
ауаптарын сәйкестендір: 