Вопросы к коллоквиуму по разделам

«Линейная алгебра», «Векторная алгебра», «Аналитическая геометрия»

1. 
   Размерность матрицы – это число строк и столбцов в ней. Обозначается индексом внизу А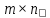
   
2. 
   Квадратной называют матрицу, у которой кол. строк равно кол.столбцов
   
3. 
   Диагональной называют матрицу, у которой все элементы вне главной диагонали равны нулю; этот термин обычно относится к квадратным матрицам. Элементы главной диагонали могут быть как нулевыми, так и ненулевыми
   
4. 
   Матрица является треугольной, если под или над главной диагональю все нули
   
5. 
   Две матрицы равны, если они имеют одинаковое количество строк и столбцов, а также одинаковое количество элементов.
   
6. 
   Складывать можно матрицы, у которых Складывать можно только матрицы одинакового размера
   
7. 
   Сумма двух матриц – это матрица, элементы которой равны суммам соответствующих элементов матриц
   
8. 
   После умножения матрицы на число получится матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на заданное число.
   
9. 
   Произведение двух матриц возможно, когда число столбцов первой (m) равняется числу строк второй (n).
   
10. 
    Обладают ли матрицы А=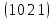 и В=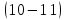 коммутативным свойством.
    
11. 
    Матрица A^T называется транспонированной к данной, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы АТ
    
12. 
    Для матрицы A_3×4 транспонированная матрица A^T имеет размерность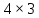
    
13. 
    Среди матриц А=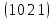 и В= 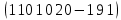больший определитель имеет В
    
14. 
    Минор элемента a₁₂ матрицы В=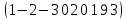 равен 0
    
15. 
    Алгебраическое дополнение элемента a₁₂ матрицы В=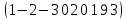 равно 0
    
16. 
    Вычислите определитель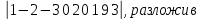 его по элементам 3-ей строки =12
    
17. 
    Вычислите определитель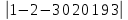 , разложив его по элементам 1-го столбца =12
    
18. 
    Если в матрице есть две одинаковые строки, то ее определитель равен нулю.
    
19. 
    Определитель треугольной матрицы равен произведению элементов её главной диагонали (в частности, определитель унитреугольной матрицы равен единице)
    
20. 
    Матрица А^–1 называется обратной для матрицы А, если при умножении этой матрицы на матрицу А как справа, так и слева получается единичная матрица: А-1 * А = А * А-1 = Е.
    
21. 
    Для единичной матрицы Е_2х2 обратная матрица имеет вид Е
    
22. 
    Метод Крамера решения системы трех линейных уравнений с тремя переменными состоит в том, что необходимо
    
23. 
    Если определитель квадратной системы линейных уравнений равен нулю, то …
    
24. 
    Матричный метод решения систем линейных уравнений состоит в том, что …
    
25. 
    Система линейных уравнений может быть решена матричным способом, если число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.
    
26. 
    Система называется несовместной, если у неё нет ни одного решения
    
27. 
    Система трех линейных уравнений с тремя переменными имеет единственное решение, если …
    
28. 
    Ранг матрицы – это наивысший порядок отличного от нуля минора этой матрицы. Ранг нулевой матрицы равен нулю
    
29. 
    Набор элементов называется линейно зависимым, если линейная комбинация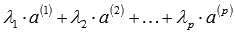 может представлять собой нулевой вектор тогда, когда среди чисел 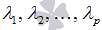есть хотя бы одно, отличное от нуля, то система векторов 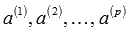называется линейно зависимой.
    
30. 
    Набор элементов называется линейно независимым, если линейная комбинация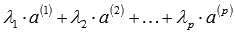 представляет собой нулевой вектор только тогда, когда все числа 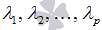равны нулю, то система векторов 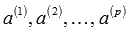называется линейно независимой.
    
31. 
    Ступенчатой называется матрица, которая удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули: где элементы отличны от нуля, а все элементы, стоящие под ними, равны нулю.
    
32. 
    Элементарными преобразования строк матрицы являются 1) перемена мест двух строк или двух столбцов в данной матрице; 2) умножение строки (или столбца) на произвольное число, отличное от нуля; 3) прибавление к одной строке (столбцу) другой строки (столбца), умноженной на некоторое число.
    
33. 
    Определение ранга матрицы через линейную независимость строк (столбцов) следующее …
    
34. 
    Основная идея метода Гаусса решения систем линейных уравнений в том, чтобы …
    
35. 
    Теорема Кронекера – Капелли.Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.
    
36. 
    Система линейных уравнений совместна и имеет единственное решение, если ранг этой системы равен количеству переменных.
    
37. 
    Система линейных уравнений совместна и имеет бесконечное множество решений, если ранг этой системы меньше количества переменных.
    
38. 
    Система линейных уравнений несовместна, если у неё нет ни одного решения
    
39. 
    Если система 3–х линейных уравнений с пятью переменными имеет бесконечное множество решений и ранг матрицы равен 3, то ее общее решение имеет вид …
    
40. 
    Если система 3–х линейных уравнений с пятью переменными имеет бесконечное множество решений и ранг матрицы равен 3, то частное решение такой системы находят из общего, когда …
    
41. 
    Базисными называются неизвестные, которые Неизвестные, коэффициенты при которых образуют столбцы базисного минора,
    
42. 
    Свободными называются неизвестные, все кроме Неизвестные, коэффициенты при которых образуют столбцы базисного минора,
    
43. 
    Вектор - это математический объект, характеризующийся величиной и направлением.
    
44. 
    Длина вектора – это длина направленного отрезка, определяющего вектор.
    
45. 
    Линейные операции над векторами – это сложение векторов, вычитание и умножение вектора на число (скаляр)
    
46. 
    Операция сложения векторов обладает свойствами a + b = b + a (коммутативность), (a + b) + c = a + (b + c) (ассоциативность), a + 0 = a (наличие нулевого элемента), a + (-a) = 0 (наличие противоположного элемента), где 0 - нулевой вектор, -a есть вектор, противоположный вектору a. Разностью a - b векторов a и b наз. вектор x такой, что x + b = a.
    
47. 
    Операция умножения вектора на число обладает свойствами ассоциативности
    
48. 
    Два вектора называют коллинеарными, если они лежат на одной прямой или на паралельных прямых
    
49. 
    Три вектора называют компланарными, если они лежат в одной или параллельных плоскастях
    
50. 
    Векторы называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору
    
51. 
    Базис векторов на плоскости – это упорядоченная пара неколлинеарных векторов отложенных от одной точки
    
52. 
    Базис векторов в пространстве – это упорядоченная тройка некомпланарных векторов отложенных от одной точки
    
53. 
    Декартова система координат на плоскости задается единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей
    
54. 
    Координаты вектора в базисе – это коэффициенты в разложении по базисным векторам
    
55. 
    Трехмерный ортонормированный базис, образуют векторы, которые попарно ортогональны и длина каждого из них равна единице
    
56. 
    Если два вектора заданы своими координатами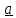 (х_а; у_а; z_a) 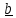(х_b; у_b; z_b), то сумма этих векторов имеет координаты ( )
    
57. 
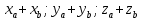    Три вектора образуют правую (левую) тройку, если смешанное произведение этих векторов больше нуля; и левой – если смешанное произведение меньше нуля.
    
58. 
    Направляющими косинусами вектора называют косинусы углов, которые вектор образует с положительными полуосями координат.
    
59. 
    Проекция вектора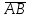 на ось 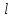- это это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-»
    
60. 
    Скалярное произведение двух векторов – это произведение их длин на косинус угла между ними
    
61. 
    Физический смысл скалярного произведения векторов в том, что работа А равна произведению производимой постоянной силой. F при перемещении тела на вектор a и составляющий с направлением силы. F угол φ. Эта связь выражается формулой: A=| F|·| a|=| F|·| a|· cosφ
    
62. 
    Скалярное произведение векторов обращается в нуль, если вектора взаимно перпендикулярны или если один сомножитель (или оба) есть нуль-векторы
    
63. 
    При перестановке векторов в скалярном произведении его величина …
    
64. 
    Cкалярное произведение векторов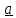 (х_а; у_а; z_a) и 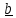(х_b; у_b; z_b) равно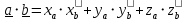
    
65. 
    Угол между векторами через скалярное произведение равен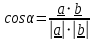
    
66. 
    Два вектора ортогональны(перпендикулярны), если если их скалярное произведение равно нулю. a · b = 0.
    
67. 
    Векторное произведение векторов – это такой третий вектор который ортогонален этим двум,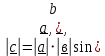 и все три вектора образуют правую тройку
    
68. 
    Векторное произведение векторов обращается в нуль, если векторы a и b коллинеарны (в частности один из них или оба-нуль-вектор)
    
69. 
    Геометрический смысл векторного произведения векторов в том, что модуль векторного произведения двух векторов есть площадь параллелограмма, построенного на этих векторах;
    
70. 
    При перестановке сомножителей в векторном произведении меняет свой знак, сохраняя модуль. Таким образом, векторное произведение не обладает переместительным свойством.
    
71. 
    Векторное произведение векторов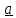 (х_а; у_а; z_a) и (х_b; у_b; z_b) выражается через координаты сомножителей …
    
72. 
    Если два вектора коллинеарны, то их векторное произведение равно нулевому вектору
    
73. 
    Площадь треугольника, построенного на двух векторах равна половине модуля векторного произведения этих векторов: SΔ =1/2 | a × b|
    
74. 
    Смешанное произведение векторов – это исло, равное скалярному произведению векторного произведения векторов a и b на вектор c. abc = (a × b)c.
    
75. 
    Смешанное произведение векторов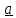 , , 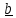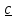не изменится, если в нем поменять местами знаки векторного и скалярного умножения
    
76. 
    Геометрический смысл смешанного произведения векторов в том, что объем параллелепипеда, который построен с помощью трех векторов u, v, w представляет собой модуль смешанного произведения этих векторов: V = | (u, v, w) | = | u ⋅ (v × w)|. Пирамида, которая построена на трех векторах u, v, w обладает объемом, равным: V = | (u, v, w) | = | u ⋅ (v × w)|
    
77. 
    Если смешанное произведение векторов обращается в нуль, то вектора компланарны
    
78. 
    Если треугольная пирамида построена на трех векторах исходящих из одной вершины, то ее объем равен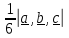
    
79. 
    Смешанное произведение векторов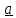 (х_а; у_а; z_a), 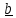(х_b; у_b; z_b), 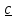(х_с; у_с; z_с) выражается через координаты сомножителей …
    
80. 
    Уравнение прямой линии с угловым коэффициентом имеет вид y (x) = k x + b. В этом уравнении k — это угловой коэффициент прямой, характеризующий угол наклона прямой к оси х, он равен тангенсу угла прямой с осью абсцисс.
    
81. 
    Общее уравнение прямой линии на плоскости имеет вид ax + by + c = 0, где a, b, c = const
    
82. 
    Уравнение прямой линии в отрезках имеет вид x a + y b = 1, где a и b не равны нулю.
    
83. 
    Пучок прямых линий, проходящих через точку А(1; 2) имеет вид ….
    
84. 
    Уравнение прямой, проходящей через две заданные точки А(1; 2) и В(4; 5) имеет вид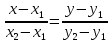
    
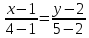
85. 
    Прямая, которая параллельна прямой у=2х+3 и проходит через точку А(4; 5), имеет уравнение y - y0 = k(x - x0)Подставляя x0 = 4, k = 2, y0 = 5 получим: y-5 = 2(x-4) или y = 2x -3
    
86. 
    Прямые у=к₁·х+b и у=к₂·х+c перпендикулярны, если k1 · k2 = −1
    
87. 
    Если на плоскости заданы прямые у=к₁·х+b и у=к₂·х+c, то угол между этими прямыми можно найти через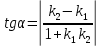
    
88. 
    Эллипс – это множество точек плоскости, для которых сумма расстояний до двух данных точек той же самой плоскости постоянна и больше чем расстояние между этими точками. Такие точки называются фокусами эллипса, а расстояние между ними фокальным расстоянием.
    
89. 
    Каноническое уравнение эллипса имеет вид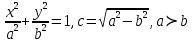
    
90. 
    Эксцентриситет эллипса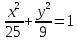 равен …
    
91. 
    Координаты фокусов эллипса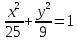 равны …
    
92. 
    Основное свойство точек эллипса в том, что ….
    
93. 
    Эксцентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на 2 обозначается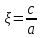
    
94. 
    Гипербола – это множество точек плоскости, для которых модуль разности расстояний от двух точек (фокусов) — величина постоянная и меньшая, чем расстояние между фокусами.
    
95. 
    Каноническое уравнение гиперболы имеет вид x²/a² - y²/b²=1
    
96. 
    Мнимая полуось гиперболы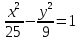 – это …
    
97. 
    Основное свойство точек гиперболы в том, что точки гиперболы нет в полосе, ограниченной прямыми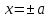
    
98. 
    Эксцентриситет гиперболы принимает значения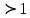
    
99. 
    Координаты фокусов гиперболы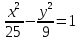 равны ….
    
100. 
     Вершины гиперболы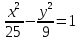 равны …
     
101. 
     Парабола – это множество точек плоскости, для которых расстояние до фиксированной точки равно расстоянию до фиксированной прямой, не проходящей через эту точку. Фиксированная точка называется фокусом, а фиксированная прямая — директрисой параболы.
     
102. 
     Каноническое уравнение параболы имеет вид : y2 = 2px, где p - расстояние от фокуса до директрисы параболы.
     
103. 
     Основное свойство точек параболы в том, что …
     
104. 
     Директриса параболы – это прямая линия кратчайшее расстояние от которой до любой точки, принадлежащей параболе, точно такое же, как расстояние от этой точки до фокуса.
     
105. 
     Директриса параболы х=4у² имеет уравнение ….
     
106. 
     Общее уравнение плоскости имеет вид .A x+B y+C z+D= Ax+By+Cz+D = 0
     
107. 
     Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1
     
108. 
     Уравнение плоскости, проходящей через три точки А(1; 2; 3), В(–1, 2; 4), С(2; –3; 5), имеет вид
     
109. 
     Две плоскости параллельны, если две плоскости не имеют общих точек
     
110. 
     Если плоскость задана уравнением х–у+2z +3=0, то вектор нормали ….
     
111. 
     Две плоскости перпендикулярны, если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости
     
112. 
     Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости.
     
113. 
     Расстояние от точки А (1; 2; 3) до плоскости 2х–у+2z +4=0 равно …
     
114. 
     Общее уравнение прямой в пространстве имеет вид …
     
115. 
     Канонические уравнения прямой в пространстве – это уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору
     
116. 
     Уравнение прямой, проходящей через точки А(1; 2; 3) и В(–1, 2; 4), имеет вид ….
     
117. 
     Угол между двумя прямыми с направляющими векторами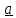 (1; 2; 2), (–1; 2;–2) равен …
     
118. 
     Прямые, заданные в пространстве каноническими уравнениями, параллельны, если …
     
119. 
     Прямые, заданные в пространстве каноническими уравнениями, перпендикулярны, если …
     
120. 
     Расстояние от точки А(1; 2; 3) до прямой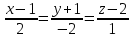 равно …
     

---

---

Смотрите также файлы

• 1 Ознакомление с предприятием с организационнораспорядительными документами.docx

• Урок игра Путешествие в страну Безопасности.doc

• Отчет по лабораторной работе 6 измерение и исследование депрессии вентиляционного участка студент.docx

• Уроков с опорой на чеклист. Предмет, класс Тема анализируемого учебного занятия Деятельность учителя Деятельность обучающихся.docx

• Какие основания послужили для признания исковых требований! Для решения этой задачи используйте следующие правовые акты.docx