Файл: 2 Точность информации это.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 18.03.2024

Просмотров: 28

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

-6FF7

93.11.13 Дана таблица истинности, в которой пропущены некоторые значения. Каким логическим функциям она может соответствовать:



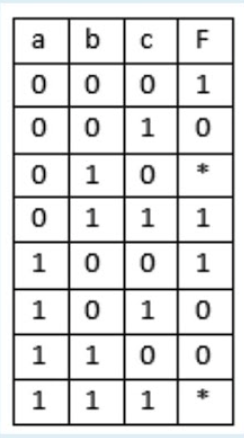
- F = 98, F = 99

94.11.13. Логическая функция задана аналитическим способом



Какая векторная запись соответствует данной функции:

- DE

95.11.13. Логическая функция задана аналитическим способом



Какая векторная запись соответствует данной функции:

- А6

96.11.13. Логическая функция задана аналитическим способом


Какая векторная запись соответствует данной функции:

-35
97.11.13. Какой из всех перечисленных способов задания логической функции является наиболее компактным для функции F = BCE4:

- векторный
98.11.13. Логическая функция задана аналитическим способом



-52


99.11.13. Логическая функция задана аналитическим способом



- 11010001
100.11.12. Допустимой схемой мультиплексора 4-1 является изображение на рисунке:

-

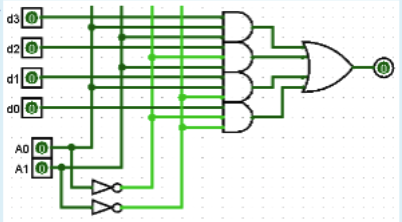
101.11.13. Какой из перечисленных способов не является способом задания логической функции:

- периодический
102.11.13. Совершенной дизъюнктивной нормальной формой называется:

- дизъюнкция совершенных конъюнкций, где ни одна совершенная КОНЬЮНКЦИЯ не повторяется
103.11.13. Дано K логических переменных. Сколько возможно построить уникальных логических функция^

- 2**2**k
104.11.12. На скольких наборах значений аргументов функция, заданная векторным способом как F = E4 принимает значение 1
105.11.13. Логическая функция задана аналитическим способом

Какая векторная запись соответствует данной функции:

- 08
106.11.13. Совершенной конъюнктивной нормальной формой называется:


- конъюнкция совершенных дизъюнкций, где ни одна совершенная дизъюнкция не повторяется
107.11.13. Дано K логических переменных. Сколько возможно записать уникальных комбинаций значений этих переменных:

-2**K

108.11.13. Логическая функция задана вектором F = A3. Укажите СКНФ:

-
109.11.13. Сколько логических переменных необходимо для построения логической функции F = 7A:
110.11.13. F = A3. Укажите СДНФ
111.11.13 Укажите верные высказывания:

1) Таблица истинности определяет истинность или ложность логической функции при всех возможных комбинациях логических переменных.

2) Таблица истинности является исчерпывающем способом задания логической функции

- Оба высказывания верны
112.11.13. Логическая функция задана аналитическим способом



Какая векторная запись соответствует данной функции

- 96
113.11.13 Минтерм это:

- логическая функция, принимающая значение единицы только на одном наборе значений аргументов.

14 - 15
114.14.15. Приведите логическую функцию к базису И-НЕ

-

115.14.15. Постройте СКНФ функции
и приведите её к базису И-НЕ

-

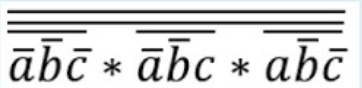
116.14.15. Постройте СКНФ функции и приведите её к базису И-НЕ

117.14.15. Приведите логическую функцию к базису ИЛИ-НЕ

-
118.14.15. Приведите логическую функцию к базису ИЛИ-НЕ

-

119.14.15. Постройте СДНФ функции и приведите её к базису И-НЕ
-
120.14.15. Постройте СДНФ функции и приведите её к базису ИЛИ-НЕ

-

121.14.15. Укажите НЕВЕРНО выполненные логические преобразования

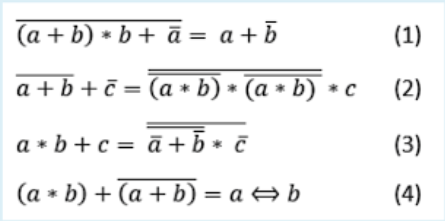- 1 и 2 - НЕПРАВИЛЬНО

122.14.15. Какой логической функции соответствует данная таблица истинности:

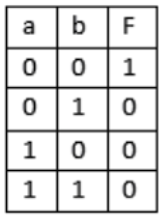- Стрелка Пирса

123.14.15. Что такое минимальный логический базис:

- минимально необходимый набор логических функций, через которые…
124.14.15. Какое(-ие) из данных выражений являются вариациями закона де Моргана:



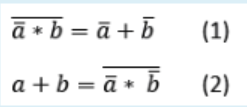
-Только выражение 2
125.14.15. Приведите логическую функцию к базису И-НЕ

-


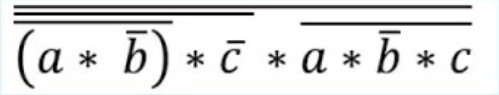
128.14.15. Постройте СКНФ функции и приведите её к базису ИЛИ-НЕ

-
129.14.15. Укажите неверно выполненное логическое преобразование:

-


130.14.15 Постройте СДНФ функции и приведите к базису И-НЕ



-
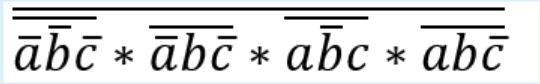
131.14.15. Постройте СКНФ функции и приведите к базису ИЛИ-НЕ

-



132.14.15. Какой логической функции соответствует данная таблица истинности:

- Штрих Шеффера
16 – 17
133.16.17. При минимизации частично определенных функций неопределенные значения логической функции, обычно обозначаемые звёздочками, интерпретируются на карте Карно так, чтобы:

- увеличить размер существующих интервалов, но не создавать новых
134.16.17. МДНФ имеет более простой вид, чем МКНФ. Насколько справедливо данное утверждение:

- справедливо для некоторых функций
135.16.17. Предположим, что имеется функция от 6-ти переменных, которая минимизируется при помощи карты Карно. На карте был выделен интервал размера 4, состоящий из единичных значений функции. Каким количеством переменных будет описан минимальный конъюнкт, соответствующий этому интервалу:

- 4
136.16.17. Операция склеивания осуществляется между двумя совершенными конъюнктами или дизъюнктами, у которых:

- Совпадают все литералы, кроме одного
137.16.17. На карте Карно значения логической функции из таблицы истинности переупорядочиваются таким образом, что переход из одной ячейки карты в другую по вертикали или горизонтали связан:

- С изменением значения только одной переменной
138.16.17. Расшифровать аббревиатуру МКНФ:

- Минимальная конъюнктивная нормальная форма

139.16.17. МКНФ – это:

- Конъюнкция минимального числа дизъюнкций переменных, взятых с отрицанием или без
140.16.17. Сколько переменных упрощается на интервале размера 4, построенном на карте Карно:

- 2
141.16.17. МДНФ – это:

- Дизъюнкция минимального числа конъюнкций переменных, взятых с отрицанием или без
142.16.17. Сколько переменных упрощается на интервале размера 8, построенном на карте Карно:

- 3

143.16.17. Укажите суммарное количество дизъюнкций и конъюнкций, необходимых для записи формулы МКНФ функции согласно её карте Карно:

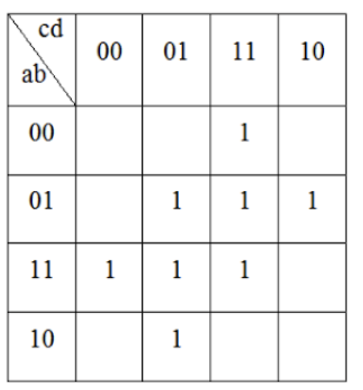- 13

144.16.17. Укажите суммарное количество дизъюнкций и конъюнкций, необходимых для записи формулы МДНФ функции согласно её карте Карно:



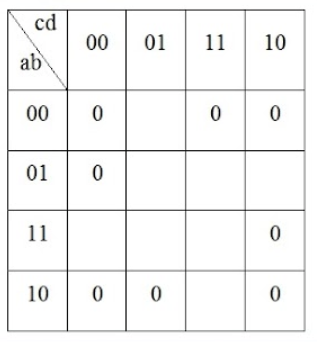
- 8
145.16.17. В чём заключается задача минимизации логической функции:

- В том, чтобы найти НАИБОЛЕЕ компактное её представление в виде нормальной формы МИНИМАЛЬНОЙ сложности
146.16.17. Расшифровать аббревиатуру МДНФ:

- Минимальная дизъюнктивная нормальная форма
147.16.17. Укажите верную формулу МКНФ функции согласно её карте Карно

-

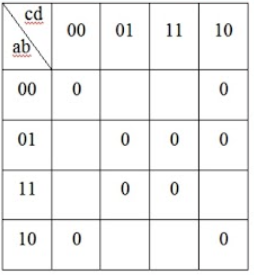148.16.17. Сколько вариантов записи МДНФ существует для указанной карты Карно:




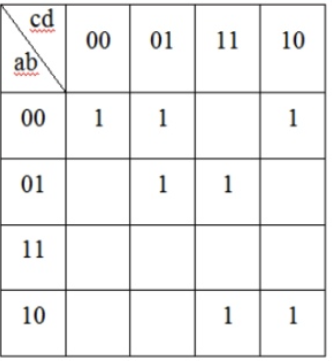
149.16.17. Укажите верную формулу МКНФ функции согласно её карте Карно:

-

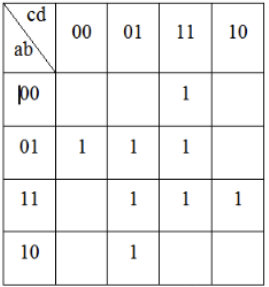150.16.17. Укажите верное заполнение карты Карно для функции 51 в 16:

-



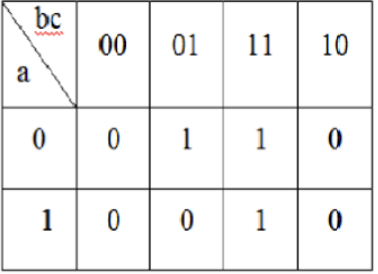
151.16.17. Сколько переменных упрощается на интервале размера 3, выделенном на карте Карно:

- Такого интервала не существует
152.16.17. Карта Карно – графический способ минимизации логических функция, который работает на основе:

- Правил склеивания и поглощения

Смотрите также файлы