ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.03.2024
Просмотров: 56
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Сабақ жоспары
Бекітемін:
| Мұғалімнің аты-жөні: | | |||||||
| Пән/Сынып: | 9 сынып | |||||||
| Күні: | | |||||||
| Тарау немесе бөлім атауы: | 9.3А Үшбұрыштарды шешу | |||||||
| Сабақтың тақырыбы: | Синустар теоремасы. | |||||||
| Оқу мақсаты: | 9.1.3.7 синустар теоремасын білу және қолдану; | |||||||
| Бағалау критериі: | -Синустар теоремасын есеп шығаруда қолдану. | |||||||
| Саралап оқыту тапсырмалары | ||||||||
| Ұжымдық жұмыс Жаңа тақырыптың түсіндірілуі Сабақ мақсаты мен бағалау критерийлерін таныстыру; Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату | Бірлескен жұмыс (1,2,3 тапсырма) Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету Бекітуге арналғантапсырмаларды орындату; Тапсырмалардың жауаптарын жазу. | Жеке жұмыс Тапсырманы ұсыну, оқушылар өз бетімен орындауы | ||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||
| 3 минут | Ұйымдастыру | Сәлеметсіздерме! Бүгін, Синустар теоремасы тақырыбын қарастырамыз - Синустар теоремасы. - Синустар теоремасын есеп шығаруда қолдану Бүгінгі сабақта меңгеретініңіз: . Үйге тапсырмасын тексеру. Өтілген тақырып тапсырмаларын тексеру Бағалау: Ауызша бағалау. | Амандасады, тақырыпты жазады. Сұрақтарға жауап береді |  | Whatsapp месенжерін қолдану. | |||
| 5 мин | Жаңа сабақты бекіту | Сұрақтар. 1.Синустар теоремасын айтыңыз. 2. Косинустар теоремасын айтыңыз. 3. Синустар теоремасын жазыңыз. 4. Косинустар теоремасын жазыңыз. 5. sin30°, Sin45°, Sin 60° - мәндері неге тең? 6. cos 30°cos 45°cos 60° - мәндері неге тең? 7. Косинустар теоремасын түрлендіріп жазыңыз. 8. Үшбұрыштарды шешу дегеніміз не? 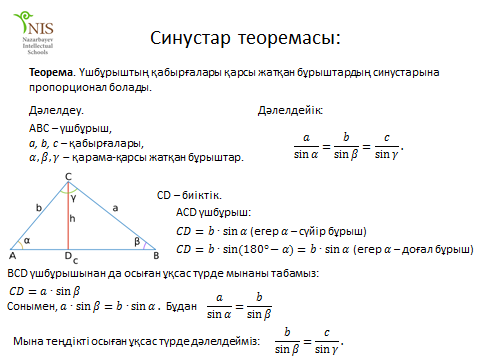 | Тақырып бойынша ресурстарды қарап, танысады Қажетті анықтамаларды жазып, сызбаны сызады. | | https://onlinemektep.net/schedule/28.01.2021/lesson/fbbceccb-22c3-48ee-b925-d752300aac8a | |||
| 25 минут | Бекіту тапсырмасы | Тапсырма. Есептер жинағынан  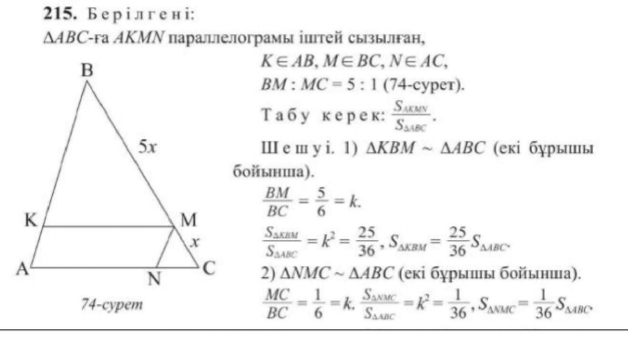 Әр оқушыға тест тапсырмасы беріледі 1. 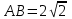 , ,  болатын ABC тік бұрышты үшбұрышына сырттай сызылған шеңбердің радиусын табыңыз. болатын ABC тік бұрышты үшбұрышына сырттай сызылған шеңбердің радиусын табыңыз.A) 1 B) 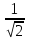 C) 2 D) C) 2 D) 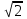 E) E)  2. Радиусы 10-ға тең шеңбердің центрінен ұзындығы 12-ге тең хордасына дейінгі қашықтықты табыңыз. A) 6.B) 8.C) 10.D) 9. E) 12. 3. Үшбұрыштың  төбелері берілген. Үшбұрыштың бұрыштарының косинусын есептеңіз. төбелері берілген. Үшбұрыштың бұрыштарының косинусын есептеңіз.А) 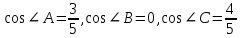 В) 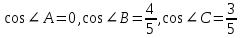 С) 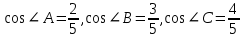 Д) 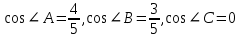 Е) 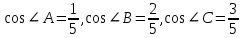 Оқулықтан №6, №8, №9. | Оқушылар есептің сызбасын сызады. үшбұрыштың белгісіз элементтерін анықтайды, есептің шешімін табады Оқулықтан есеп шығарады. Білім алушы дескрипторға сәйкес тапсырмаларды орындайды. | Дескриптор: -Үшбұрыштың бұрыштарын табады - синустар теоремасын қолданады Дескриптор: Есептің шартына байланысты теореманы дұрыс таңдайды; Формуланы дұрыс жазады; Белгісіз шаманы табады; Жауабын жазады. ҚБ:  -Тақырыпқа қатысты есептерді талдайды. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |||
| 5 мин | Жеке жұмыс | Тест тапсырмасы | Тапсырманы орындайды | | | |||
| 2 минут | | Бүгінгі сабақта: - Синустар теоремасы. - Синустар теоремасын есеп шығаруда қолдану Кері байланыс. Бүгін сабақта мен.....үйрендім Бүгін сабақта маған....ұнады Бүгін сабақта мен.....қайталадым Бүгін сабақта мен өзіме....деген баға қойдым Үйге тапсырма. №10. | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Whatsapp месенжерін қолдану Презентация | |||
Сабақ жоспары
Бекітемін:
| Мұғалімнің аты-жөні: | | |||||||||||||
| Пән/Сынып: | 9 сынып | |||||||||||||
| Күні: | | |||||||||||||
| Тарау немесе бөлім атауы: | 9.3А Үшбұрыштарды шешу | |||||||||||||
| Сабақтың тақырыбы: | Синустар теоремасы. | |||||||||||||
| Оқу мақсаты: | 9.1.3.7 синустар теоремасын білу және қолдану; | |||||||||||||
| Бағалау критериі: | -Синустар теоремасын есеп шығаруда қолдану. | |||||||||||||
| Саралап оқыту тапсырмалары | ||||||||||||||
| Ұжымдық жұмыс Жаңа тақырыптың түсіндірілуі Сабақ мақсаты мен бағалау критерийлерін таныстыру; Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату | Бірлескен жұмыс (1,2,3 тапсырма) Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету Бекітуге арналғантапсырмаларды орындату; Тапсырмалардың жауаптарын жазу. | Жеке жұмыс Тапсырманы ұсыну, оқушылар өз бетімен орындауы | ||||||||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||||||||
| 3 минут | Ұйымдастыру | Сәлеметсіздерме! Бүгін, Синустар теоремасы тақырыбын қарастырамыз - Синустар теоремасы. - Синустар теоремасын есеп шығаруда қолдану Бүгінгі сабақта меңгеретініңіз: . Үйге тапсырмасын тексеру. Өтілген тақырып тапсырмаларын тексеру Бағалау: Ауызша бағалау. | Амандасады, тақырыпты жазады. Сұрақтарға жауап береді |  | Whatsapp месенжерін қолдану. | |||||||||
| 5 мин | Жаңа сабақты бекіту | Сұрақтар. 1.Синустар теоремасын айтыңыз. 2. Косинустар теоремасын айтыңыз. 3. Синустар теоремасын жазыңыз. 4. Косинустар теоремасын жазыңыз. 5. sin30°, Sin45°, Sin 60° - мәндері неге тең? 6. cos 30°cos 45°cos 60° - мәндері неге тең? 7. Косинустар теоремасын түрлендіріп жазыңыз. 8. Үшбұрыштарды шешу дегеніміз не? Теорема:Үшбұрыштың қабырғалары қарсы жатқан бұрыштардың синустарына пропорционал болады Ү 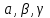 шбұрыштың қабырғалары қарсы жатқан бұрыштарының синустарына пропорционал болады, яғни ΔАВС үшбұрыштарының а, в, с қабырғаларына қарсы жатқан бұрыштары болса, онда шбұрыштың қабырғалары қарсы жатқан бұрыштарының синустарына пропорционал болады, яғни ΔАВС үшбұрыштарының а, в, с қабырғаларына қарсы жатқан бұрыштары болса, онда 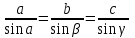 теңдігі орындалады. Б 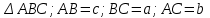 ерілгені: ерілгені: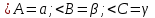 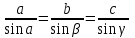 Д/к Дәлелдеу үшін: СД биіктік түсірейік. 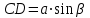 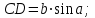 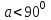 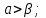 болсын ; болсын ; 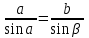 ; ; б 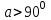 олса да бола алмайды. олса да бола алмайды.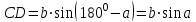 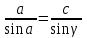 Осы сияқты В төбесінен биіктігін түсіру 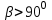 арқылы дәлелдеуге болады. | Тақырып бойынша ресурстарды қарап, танысады Қажетті анықтамаларды жазып, сызбаны сызады. 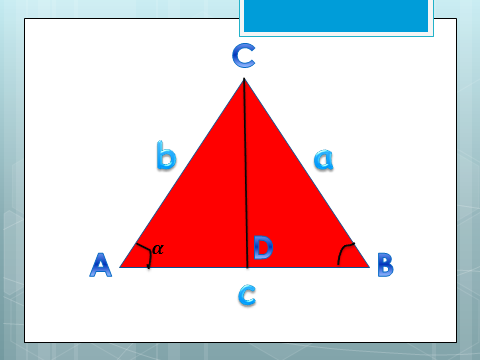 | | https://onlinemektep.net/schedule/28.01.2021/lesson/fbbceccb-22c3-48ee-b925-d752300aac8a | |||||||||
| 25 минут | Бекіту тапсырмасы | Тапсырма. Есептер жинағынан №1 АВС үшбұрышы берілген. ے С=300, ے В=450 , АВ=4 см болса, АС қабырғасының ұзындығын табу керек. №2 АВС үшбұрышында А,В,С бұрыштарының қатынасы 1:2:3 қатынасындай және ВС =8 см. АВ және АС қабырғаларының ұзындығын табыңдар. Жауаптары 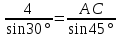 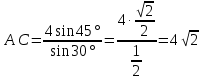 ےА=300, ے В=600ے С=900, 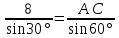 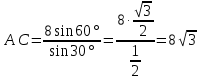 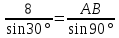 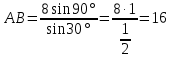 №3 АВС үшбұрышының ВС және АС қабырғалары мен ВС қабырғасына қарсы А бұрышы берілген. Қалған бұрыштары мен үшінші қабырғасын табу керек.
Оқулықтан №11, №13. | Оқушылар есептің сызбасын сызады. үшбұрыштың белгісіз элементтерін анықтайды, есептің шешімін табады Оқулықтан есеп шығарады. Білім алушы дескрипторға сәйкес тапсырмаларды орындайды. | Дескриптор: -Үшбұрыштың қабырғаларын табады - синустар теоремасын қолданады Дескриптор: Есептің шартына байланысты теореманы дұрыс таңдайды; Формуланы дұрыс жазады; Белгісіз шаманы табады; Жауабын жазады. ҚБ:  -Тақырыпқа қатысты есептерді талдайды. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |||||||||
| 5 мин | Жеке жұмыс | Жеке жұмыс І Есептер шығару: 1. a = 20, b = 7, c = 27, cos 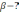 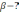 2. Үшбұрыштың a=7м, b=5м қабырғаларымен а қабырғасына қарсы жатқан 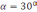 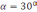 бұрышы берілген. B қабырғасына қарсы жатқан бұрышы берілген. B қабырғасына қарсы жатқан 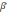 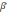 бұрышының синусын табыңдар. бұрышының синусын табыңдар.3. АВС үшбұрышының қабырғасы және екі бұрышы берілген. Оның үшінші бұрышы мен қалған екі қабырғасын есептеңдер.ВС 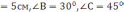 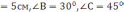 4. a=16, b=10, 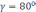 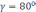 . Табу керек: с, . Табу керек: с, 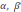 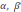 | Тапсырманы орындайды | | | |||||||||
| 2 минут | | Бүгінгі сабақта: - Синустар теоремасы. - Синустар теоремасын есеп шығаруда қолдану Кері байланыс.
Үйге тапсырма. №15. | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Whatsapp месенжерін қолдану Презентация | |||||||||
Сабақ жоспары
Бекітемін:
| Мұғалімнің аты-жөні: | | |||||||
| Пән/Сынып: | 9 сынып | |||||||
| Күні: | | |||||||
| Тарау немесе бөлім атауы: | 9.3А Үшбұрыштарды шешу | |||||||
| Сабақтың тақырыбы: | Іштей сызылған үшбұрыш пен сырттай сызылған көпбұрыштың аудандары. | |||||||
| Оқу мақсаты: | 9.1.3.8 іштей сызылған үшбұрыштың ауданын ( 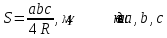 – үшбұрыштың қабырғалары, – үшбұрыштың қабырғалары, 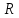 – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының ( – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының (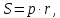 мұндағы мұндағы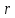 – іштей сызылған шеңбер радиусы, – іштей сызылған шеңбер радиусы, 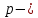 көпбұрыштың жарты периметрi) формуларын біледі және қолданады көпбұрыштың жарты периметрi) формуларын біледі және қолданады | |||||||
| Бағалау критериі: | 9.1.3.8 іштей сызылған үшбұрыштың ауданын ( 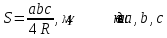 – үшбұрыштың қабырғалары, – үшбұрыштың қабырғалары, 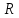 – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының ( – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының (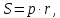 мұндағы мұндағы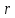 – іштей сызылған шеңбер радиусы, – іштей сызылған шеңбер радиусы, 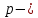 көпбұрыштың жарты периметрi) формуларын біледі және қолданады көпбұрыштың жарты периметрi) формуларын біледі және қолданады | |||||||
| Саралап оқыту тапсырмалары | ||||||||
| Ұжымдық жұмыс Жаңа тақырыптың түсіндірілуі Сабақ мақсаты мен бағалау критерийлерін таныстыру; Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату | Бірлескен жұмыс (1,2,3 тапсырма) Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету Бекітуге арналғантапсырмаларды орындату; Тапсырмалардың жауаптарын жазу. | Жеке жұмыс Тапсырманы ұсыну, оқушылар өз бетімен орындауы | ||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||
| 3 минут | Ұйымдастыру | Сәлеметсіздерме! Бүгін, Іштей сызылған үшбұрыш пен сырттай сызылған көпбұрыштың аудандары тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -шеңберге іштей сызылған үшбұрыш ауданының формуласы. -шеңберге іштей сызылған үшбұрыш ауданының формуласын есептер шығаруда қолдану. Үйге тапсырмасын тексеру. Өтілген тақырып тапсырмаларын тексеру Бағалау: Ауызша бағалау. | Амандасады, тақырыпты жазады. Сұрақтарға жауап береді |  | Whatsapp месенжерін қолдану. | |||
| 5 мин | Жаңа сабақ | Бұрыш жазықтықты екі бөлікке бөледі. Бұл бөліктердің әр қайсысы бұрыш деп аталады. Қабырғалары а және b сәулелері болатын АОВ және ВОА бұрыштары кескінделген. Қабырғалары ортақ бұрыштар бір-біріне толықтауыш бұрыштар деп аталады. ВОА бұрышы АОВ бұрышына немесе АОВ бұрышы ВОА бұрышына толықтауыш бұрыштар. 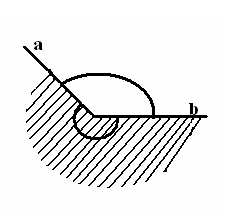 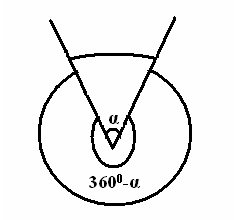 Егер бұрыштардың біреуінің градустық өлшемі α – ға тең болса, онда толықтауыш бұрыштың градустық өлшемі 3600- α болады. Төбесі шеңбердің центрінде жататын бұрыш центрлік бұрыш деп аталады. Бұрыштың ішінде орналасқан шеңбер бөлігі осы центрлік бұрышқа сәйкес шеңбер доғасы деп аталады. АКВ доғасы АОВ центрлік бұрышына сәкес. Шеңбер доғасының градустық өлшемі деп оған сәйкес центрлік бұрыштың градустық өлшемін атайды. 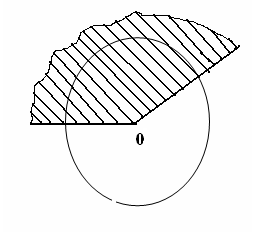 Төбесі шеңберде жататын, ал қабырғалары сол шеңберді қиып өтетін бұрыш шеңберге іштей сызылған бұрыш деп аталады. 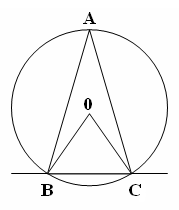 АВС бұрышы шеңберге іштей сызылған . Оның В төбесі шеңбер бойында жатыр, ал бұрыштың қабырғалары шеңберді А және С нүктелерінде қиып өтеді. А және С нүктелері шеңберді екі доғаға бөледі. В нүктесі жатпайтын доғаға сәйкес центрлік бұрыш іштей сызылған В бұрышына сәйкес центрлік бұрыш деп аталады. Сонымен шеңберге іштей сызылған АВС бұрышына сәйкес центрлік бұрыш АОС бұрышы болады. Теорема: Шеңберге іштей сызылған бұрыш өзіне сәйкес центрлік бұрыштың жартысына тең болады. Теореманы дәлелдеу үшін 3 жағдайды қарастырамыз: 1. Бұрыштың бір қабырғасы шеңбердің центрінен өтеді. АО радиусын жүргізсек, теңбүйірлі АВО үшбұрышы шығады, мұнда АО=ОВ, сондықтан 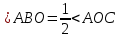 2. Шеңбердің О центрі шеңберге іштей сызылған бұрыш қабырғаларының арасында жатады. ВD диаметрін жүргіземіз, сонда 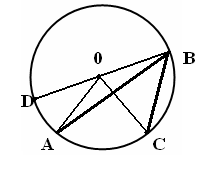 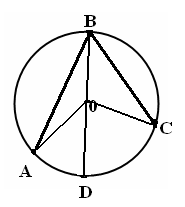 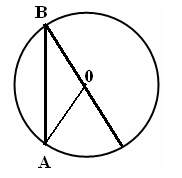 3. Шеңбердің О центрі шеңберге іштей сызылған АВС бұрышынан тысқары жатсын. ВD диаметрін жүргіземіз, сонда Теорема дәлелденді. | Тақырып бойынша ресурстарды қарап, танысады Қажетті анықтамаларды жазып, сызбаны сызады. | | https://onlinemektep.net/schedule/02.02.2021/lesson/ed5df345-cc94-436b-92c8-e88efb6faf1f | |||
| 25 минут | Бекіту тапсырмасы | Тапсырма. №9. Шеңбердің АС және ВС доғалары сәйкесінше 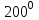 және және 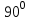 -қа тең. Іштей сызылған АСВ бұрышын табыңдар. -қа тең. Іштей сызылған АСВ бұрышын табыңдар. Бер: Шеңбер 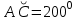 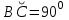 Табу керек: Іштей сызылған 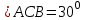 ? ?Шешуі: 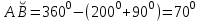 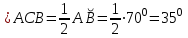 Жауабы: 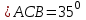 №10. Хорда шеңберді екі доғаға бөледі. Бұл доғалардың шамаларының қатынастары 4:5 болса, осы хорда шеңбердің бойындағы нүктелерден қандай бұрышпен көрінеді? Бер: Шеңбер Хорда шеңберді екі доғаға бөледі Доғалардың шамаларының қатынастары 4:5 Табу керек: Доғалардың шамаларының қатынастары Шешуі:
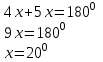 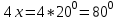 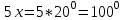 Жауабы: 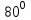 және және 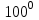 №11. АС хордасы шеңбердің доғасын 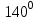 -қа кереді. Осы хорда мен шеңберге С нүктесінде жүргізілген жанаманың арасындағы АСВ бұрышын табыңдар. -қа кереді. Осы хорда мен шеңберге С нүктесінде жүргізілген жанаманың арасындағы АСВ бұрышын табыңдар. Бер: Шеңбер АС хорда АС хордасы шеңбердің доғасын 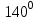 -қа кереді -қа кередіТабу керек: 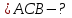 Шешуі: 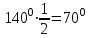 Жауабы: 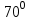 Оқулықтан №1,3,5. | Оқушылар есептің сызбасын сызады. үшбұрыштың белгісіз элементтерін анықтайды, есептің шешімін табады Оқулықтан есеп шығарады. Білім алушы дескрипторға сәйкес тапсырмаларды орындайды. | Дескриптор: -Үшбұрыштың қабырғаларын табады - синустар теоремасын қолданады Дескриптор: Есептің шартына байланысты теореманы дұрыс таңдайды; Формуланы дұрыс жазады; Белгісіз шаманы табады; Жауабын жазады. ҚБ:  -Тақырыпқа қатысты есептерді талдайды. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |||
| 5 мин | Жеке жұмыс | №12.АС хордасы мен шеңберге жүргізілген ВС жанамасының арасындағы бұрыш 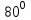 -қа тең. АС хордасымен керілген доғаның градустық шамасын табыңдар. -қа тең. АС хордасымен керілген доғаның градустық шамасын табыңдар. | Тапсырманы орындайды. Жауабы: 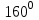 | | | |||
| 2 минут | | Бүгінгі сабақта: -шеңберге іштей сызылған үшбұрыш ауданының формуласы. -шеңберге іштей сызылған үшбұрыш ауданының формуласын есептер шығаруда қолдану. Кері байланыс: «Басбармақ» Рефлексия: - нені білдім, нені үйрендім - нені толық түсінбедім - немен жұмысты жалғастыру қажет Үйге тапсырма. №11, №12. | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Whatsapp месенжерін қолдану Презентация | |||
Сабақ жоспары
Бекітемін:
| Мұғалімнің аты-жөні: | | |||||||
| Пән/Сынып: | 9 сынып | |||||||
| Күні: | | |||||||
| Тарау немесе бөлім атауы: | 9.3А Үшбұрыштарды шешу | |||||||
| Сабақтың тақырыбы: | Іштей сызылған үшбұрыш пен сырттай сызылған көпбұрыштың аудандары. | |||||||
| Оқу мақсаты: | 9.1.3.8 іштей сызылған үшбұрыштың ауданын ( 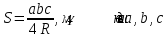 – үшбұрыштың қабырғалары, – үшбұрыштың қабырғалары, 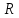 – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының ( – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының ( мұндағы мұндағы – іштей сызылған шеңбер радиусы, – іштей сызылған шеңбер радиусы,  көпбұрыштың жарты периметрi) формуларын біледі және қолданады көпбұрыштың жарты периметрi) формуларын біледі және қолданады | |||||||
| Бағалау критериі: | 9.1.3.8 іштей сызылған үшбұрыштың ауданын ( 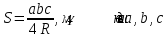 – үшбұрыштың қабырғалары, – үшбұрыштың қабырғалары, 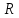 – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының ( – сырттай сызылған шеңбер радиусы) және сырттай сызылған көпбұрыштың ауданының ( мұндағы мұндағы – іштей сызылған шеңбер радиусы, – іштей сызылған шеңбер радиусы,  көпбұрыштың жарты периметрi) формуларын біледі және қолданады көпбұрыштың жарты периметрi) формуларын біледі және қолданады | |||||||
| Саралап оқыту тапсырмалары | ||||||||
| Ұжымдық жұмыс Жаңа тақырыптың түсіндірілуі Сабақ мақсаты мен бағалау критерийлерін таныстыру; Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату | Бірлескен жұмыс (1,2,3 тапсырма) Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету Бекітуге арналғантапсырмаларды орындату; Тапсырмалардың жауаптарын жазу. | Жеке жұмыс Тапсырманы ұсыну, оқушылар өз бетімен орындауы | ||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||
| 3 минут | Ұйымдастыру | Сәлеметсіздерме! Бүгін, Іштей сызылған үшбұрыш пен сырттай сызылған көпбұрыштың аудандары тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -шеңберге іштей сызылған үшбұрыш ауданының формуласы. -шеңберге іштей сызылған үшбұрыш ауданының формуласын есептер шығаруда қолдану. Үйге тапсырмасын тексеру. Өтілген тақырып тапсырмаларын тексеру Бағалау: Ауызша бағалау. | Амандасады, тақырыпты жазады. Сұрақтарға жауап береді |  | Whatsapp месенжерін қолдану. | |||
| 5 мин | Жаңа сабақ | Бұрыш жазықтықты екі бөлікке бөледі. Бұл бөліктердің әр қайсысы бұрыш деп аталады. Қабырғалары а және b сәулелері болатын АОВ және ВОА бұрыштары кескінделген. Қабырғалары ортақ бұрыштар бір-біріне толықтауыш бұрыштар деп аталады. ВОА бұрышы АОВ бұрышына немесе АОВ бұрышы ВОА бұрышына толықтауыш бұрыштар. 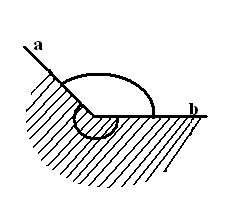  Егер бұрыштардың біреуінің градустық өлшемі α – ға тең болса, онда толықтауыш бұрыштың градустық өлшемі 3600- α болады. Төбесі шеңбердің центрінде жататын бұрыш центрлік бұрыш деп аталады. Бұрыштың ішінде орналасқан шеңбер бөлігі осы центрлік бұрышқа сәйкес шеңбер доғасы деп аталады. АКВ доғасы АОВ центрлік бұрышына сәкес. Шеңбер доғасының градустық өлшемі деп оған сәйкес центрлік бұрыштың градустық өлшемін атайды.  Төбесі шеңберде жататын, ал қабырғалары сол шеңберді қиып өтетін бұрыш шеңберге іштей сызылған бұрыш деп аталады. 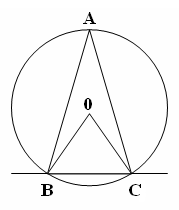 АВС бұрышы шеңберге іштей сызылған . Оның В төбесі шеңбер бойында жатыр, ал бұрыштың қабырғалары шеңберді А және С нүктелерінде қиып өтеді. А және С нүктелері шеңберді екі доғаға бөледі. В нүктесі жатпайтын доғаға сәйкес центрлік бұрыш іштей сызылған В бұрышына сәйкес центрлік бұрыш деп аталады. Сонымен шеңберге іштей сызылған АВС бұрышына сәйкес центрлік бұрыш АОС бұрышы болады. Теорема: Шеңберге іштей сызылған бұрыш өзіне сәйкес центрлік бұрыштың жартысына тең болады. | Тақырып бойынша ресурстарды қарап, танысады Қажетті анықтамаларды жазып, сызбаны сызады. | | https://onlinemektep.net/schedule/02.02.2021/lesson/ed5df345-cc94-436b-92c8-e88efb6faf1f | |||
| 25 минут | Бекіту тапсырмасы | Тапсырма. 1) Шеңберге іштей сызылған бұрыш 22030/ - қа тең. Осы бұрыш тірелетін доғаның градустық шамасын есептеңдер. 2) Шеңбер хордаларымен 1:2:3 қатынасында бөлінген. Пайда болған үшбұрыштың бұрыштарын есептеңдер. 3) Іштей сызылған АВС бұрышы АС доғасына тіреледі. АС доғасы 570- қа тең. АВС бұрышы неге тең? 4) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=5 см6 ВЕ=2 см, СЕ=2,5 см. ЕД кесіндісінің ұзындығы есептеңдер. 5) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=7 см, ВЕ=5 см, СЕ=2,5 см. ЕД кесіндісінің ұзындығы есептеңдер. 6) АВ және СД хордалары Е нүктесінде қиылысады. АЕ=8 см, ВЕ=9 см, СЕ=3,5см. ЕД кесіндісінің ұзындығы есептеңдер. Пысықтау сұрақтары. 1. Центірлік бұрыш дегеніміз не? 2. Центрлік бұрышқа сәйкес шеңбер доғасы деп қандай доғаны айтады? 3. Шеңбер доғасының градустық өлшемі қалай анықталады? 4. Шеңберге іштей сызылған бұрыш деп қандай бұрышты атайды? 5. Диаметрге тірелетін бұрыш қандай бұрыш болады? 6. Өзара қиылысатын хордалар кесінділерінің қасиеттерін дәлелдеңдер? Оқулықтан №15, №16. | Оқушылар есептің сызбасын сызады. үшбұрыштың белгісіз элементтерін анықтайды, есептің шешімін табады Оқулықтан есеп шығарады. Білім алушы дескрипторға сәйкес тапсырмаларды орындайды. | Дескриптор: -Үшбұрыштың қабырғаларын табады - синустар теоремасын қолданады Дескриптор: Есептің шартына байланысты теореманы дұрыс таңдайды; Формуланы дұрыс жазады; Белгісіз шаманы табады; Жауабын жазады. ҚБ:  -Тақырыпқа қатысты есептерді талдайды. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |||
| 5 мин | Жеке жұмыс | №12.АС хордасы мен шеңберге жүргізілген ВС жанамасының арасындағы бұрыш 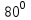 -қа тең. АС хордасымен керілген доғаның градустық шамасын табыңдар. -қа тең. АС хордасымен керілген доғаның градустық шамасын табыңдар. | Тапсырманы орындайды. Жауабы: 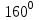 | | | |||
| 2 минут | | Бүгінгі сабақта: -шеңберге іштей сызылған үшбұрыш ауданының формуласы. -шеңберге іштей сызылған үшбұрыш ауданының формуласын есептер шығаруда қолдану. Кері байланыс: «Басбармақ» Рефлексия: - нені білдім, нені үйрендім - нені толық түсінбедім - немен жұмысты жалғастыру қажет Үйге тапсырма. №22. | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Whatsapp месенжерін қолдану Презентация | |||

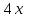
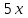 деп белгілеп аламыз
деп белгілеп аламыз