5. Объясните полученные АЧХ и ФЧХ схемы.

6. Что такое полоса пропускания? Как её измерить? Как влияют параметры схемы на полосу пропускания?

7. Объясните назначение элементов исследуемой схемы.

8. Как влияют параметры элементов схемы на коэффициент гармоник выходного сигнала?

9. Как расширить полосу пропускания в области нижних частот (уменьшить f_н)?

10. Как расширить полосу пропускания в области верхних частот (увеличить f_в)?

11. Как уменьшить нелинейные искажения в транзисторном усилительном каскаде?


ЛАБОРАТОРНАЯ РАБОТА № 3
Амплитудно-модулированные колебания
Цель работы: изучить и проанализировать характеристики амплитудно-модулированных (АМ) колебаний.
Общие положения
Перенос спектра сигналов из низкочастотной области в выделенную для их передачи область высоких частот канала связи выполняется операцией модуляции.

Амплитудная модуляция (АМ) соответствует переносу информации s(t)  U(t) при постоянных значениях параметров  и . АМ – сигнал симметричен относительно оси времени и представляет собой произведение информационной огибающей U(t) и ее заполнения гармоническим колебанием, частота которого, как правило, много выше максимальных частот в огибающей функции U(t). Форма записи амплитудно - модулированного сигнала:

u(t) = U(t)cos(_t+_o),

U(t) = U_m[1+Ms(t)],

где U_m – постоянная амплитуда несущего колебания при отсутствии входного (модулирующего) сигнала s(t), М – коэффициент амплитудной модуляции.




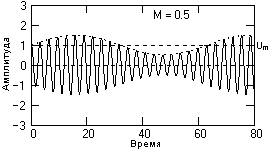
Рис. 3.1. Модулированный сигнал.
Значение коэффициента М характеризует глубину амплитудной модуляции. При значении |Мs(t)| < 1 для любых значений t форма огибающей несущего колебания полностью повторяет форму модулирующего сигнала s(t), что можно видеть на рис. 3.1 (сигнал s(t) = sin(_st), коэффициент модуляции М = 0.5). Малую глубину модуляции (М << 1) применять нецелесообразно, т.к. при этом мощность передаваемого информационного сигнала s(t) много меньше мощности несущего колебания и мощность передатчика используется неэкономично.




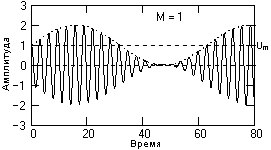
Рис. 3.2. Глубокая модуляция.
На рис. 3.2 приведен пример так называемой глубокой модуляции, при которой значение |Ms

---

_экстр(t)| стремится к 1 в экстремальных точках функции s(t). При глубокой модуляции используются также понятия относительного коэффициента модуляции вверх: M_в = (U_max - U_m)/U_m, и модуляции вниз: M_н = (U_m - U_min)/U_m. 100% - ная модуляция вверх (М_в =1) может приводить к искажениям сигналов при перегрузках передатчика, если последний имеет ограниченный динамический диапазон по амплитуде несущих частот или ограниченную мощность передатчика (увеличение амплитуды несущих колебаний в пиковых интервалах сигнала U(t) в два раза требует увеличения мощности передатчика в четыре раза).




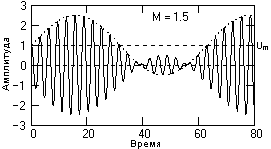
Рис. 3.3. Перемодуляция сигнала.
Относительный коэффициент модуляции вниз также должен быть достаточно надежно ограничен. При М_н > 1 возникает так называемая перемодуляция, пример которой приведен на рис. 3.3, при которой форма огибающей искажается относительно формы модулирующего сигнала.

Простейшая форма модулированного сигнала создается при однотональной амплитудной модуляции – модуляции несущего сигнала гармоническим колебанием с одной частотой :

u(t) = U_m[1+Mcos(t)]cos(_ot). (3.1)

Для упрощения математических выражений значения начальных фазовых углов несущего и модулирующего колебания здесь и в дальнейшем, если это не имеет принципиального значения, принимаем равными нулю.

С учетом известной формулы cos(x)cos(y) = (1/2)[cos(x+y)+cos(x-y)] из выражения (3.1) получаем:

u(t) = U_mcos(_ot) + (U_mM/2)cos[(_o+)t] + (U_mM/2)cos[(_o-)t].




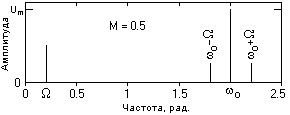
Рис. 3.4. Амплитудные спектры сигналов

при однотональной модуляции.
Отсюда следует, что модулирующее колебание с частотой  перемещается в область частоты _o и расщепляется на два колебания, симметричные относительно частоты _o, с частотами соответственно (_o+верхняя боковая частота, и (_o-нижняя боковая частота (рис. 3.4 для сигнала, приведенного на рис. 3.1). Амплитуды колебаний на боковых частотах равны друг другу и при 100%-ной модуляции равны половине амплитуды колебаний несущей частоты.

Принципиальной необходимости излучать обе боковые полосы нет, т.к. в них содержится одинаковая информация. Передача информации с помощью одной боковой полосы (ОБП) позволит экономнее использовать место в эфире, т.к. полоса излучаемого сигнала сокращается вдвое. Часто при однополосной связи подавляется нижняя полоса частот и вместе с ней излучается 15 – 20% -ный остаток несущей частоты. При этом снижается нагрузка на передатчик.

---

Недостатком связи на ОБП частот является более сложная реализация приёмной аппаратуры.
Порядок выполнения работы
1. Собрать схему 3.1, моделирующую АМ колебание.



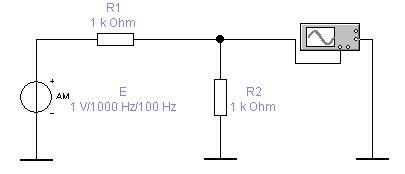
Схема 3.1.
2. Установить параметры элементов:

2.1. Генератор АМ-колебаний (AМ source) Е:

- амплитуда сигнала VC = 0.5N В;

- несущая частота FC = 1 кГц;

- модулирующая частота FM = 100 Гц;

- коэффициент модуляции М = 0.3.

2.2. Сопротивления R1 и R2 по 1 кОм каждый.

3. Перенести осциллограмму полученного колебания в отчёт. По осциллограмме определить экспериментальный коэффициент глубины модуляции, используя расчётную формулу:
М_э = .
4. С помощью пунктов меню “Analysis” → “Fourier” получить спектральную диаграмму на выходе схемы. Для этого перед началом спектрального анализа в меню “Fourier” установить:

- номер точки выходного узла схемы в окне “Output node” (заранее определяется так: подвести курсор к выходному узлу схемы, нажать правую кнопку мышки, войти в меню “Component properties”, в открывшемся окне “Node ID” прочитать номер узла);

- шаг частоты для анализа, равный частоте модулирующего сигнала (в нашем случае – 100 Гц) в окне “Fundamental frequency”;

- число гармоник “Number harmonics” равное 15.

5. Перенести спектрограмму в отчёт. Измерить и записать параметры несущей U₀, нижней U_н и верхней U_в боковых частот.

6. Рассчитать эффективность передачи информации с помощью амплитудной модуляции как отношение мощности сигналов, содержащих в себе передаваемую информацию, к общей передаваемой мощности АМ-колебания.

η_э = .

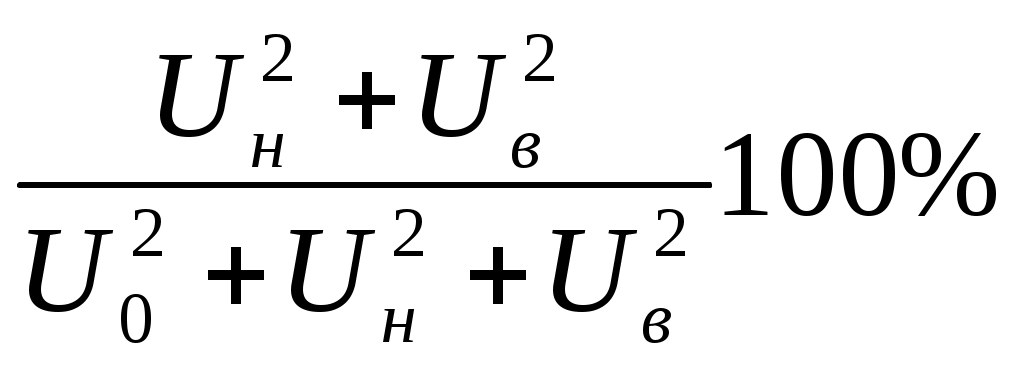7. Сравнить полученное экспериментальное значение η_э с теоретическим, которое можно рассчитать по формуле:

η_т = .
8. Повторить п.п. 3 - 7 для значений коэффициента модуляции М, равным 0.5, 1.0 и 1.5.

9. Результаты свести в таблицу.

М	ηэ	ηт
0,3
0,5
1,0
1,5

---

10. Проанализировать полученные результаты.
11. Собрать схему 3.2, моделирующую получение АМ сигнала с однополосной модуляцией.

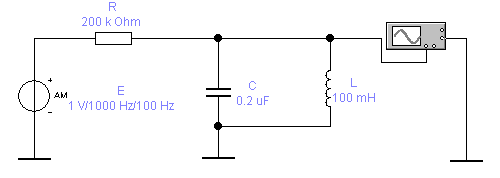
Схема 3.2.
12. Установить параметры элементов:

12.1. Генератор АМ колебаний (AМ source) Е:

- амплитуда сигнала VC = 0.5N В;

- несущая частота FC = 1 кГц;

- модулирующая частота FM = 100 Гц;

- коэффициент модуляции М = 0.3.

12.2. Сопротивление R = 200 кОм.

12.3. Индуктивность L = 0.1 Гн.

12.4. Величину ёмкости С рассчитать так, чтобы колебательный контур был настроен на частоту верхней боковой составляющей исследуемого АМ сигнала. Расчеты занести в отчёт.

13. Повторить п.п. 4 - 6 для значений коэффициента модуляции М, равным 0.5 и 1.0.

14. Результаты свести в таблицу.

М	ηом
0,3
0,5
1,0

15. Проанализировать полученные результаты и сравнить их с п. 9.

16. Заменив в схеме 3.2 источник АМ сигнала Е на генератор синусоидального напряжения, снять и перенести в отчёт АЧХ и ФЧХ схемы в диапазоне частот от 500 до 1500 Гц. Убедиться в правильности расчёта резонансной частоты LC контура.
Содержание отчёта
1. Исследуемые схемы.

2. Результаты вычислений и измерений.

3. Формы сигналов.

4. Графики полученных диаграмм.

5. Результаты проведенного анализа и выводы по работе.
Контрольные вопросы
1. Что такое амплитудная модуляция? Запишите аналитическое выражение АМ-колебания.

2. Какой спектр имеет АМ-колебание? Как можно уменьшить ширину этого спектра?

3. Что такое эффективность передачи информации с помощью амплитудной модуляции? Как улучшить этот показатель?

4. Какие недостатки двухполосного АМ колебания?

5. Почему в п.12 LC контур настраивается на частоту верхней боковой составляющей спектра АМ-колебания? Чему равна эта частота в данном случае?

6. Какие виды АМ-колебаний Вы знаете?

7. Что такое амплитудная манипуляция?

8. Как получить АМ с одной боковой полосой (ОБП)?

9. Чем отличается АМ-колебание с ОБП от двухполосной АМ?

10. Назовите преимущества и недостатки АМ-колебаний с ОБП.

11. Что такое коэффициент модуляции М? Каков его физический смысл?

---

12. Что происходит с АМ-колебанием при М > 1?

13. Что такое добротность колебательного контура? Как её рассчитать и каков её физический смысл?

14. Какая добротность колебательного контура должна быть в схеме 3.2? Почему?

ЛАБОРАТОРНАЯ РАБОТА № 4
Детектирование амплитудно-модулированных колебаний
Цель работы: изучить и проанализировать процессы при квадратичном и линейном режимах демодуляции (детектирования) амплитудно-модулированных колебаний.
Общие положения
Детектирование колебаний заключается в восстановлении управляющего сигнала, который в неявной форме содержится в модулированном высокочастотном (ВЧ) колебании. По своему назначению детектирование является процессом, обратным процессу модуляции.

В амплитудном детекторе (АД) осуществляется выделение огибающей амплитудно-модулированного сигнала с одновременным устранением несущего колебания. Роль несущих колебаний могут выполнять как гармонические колебания, так и последовательности радио- или видеоимпульсов.

В состав любого детектора входит нелинейный элемент для образования спектральных компонент, соответствующих модулирующей частоте, и линейный фильтр, для выделения компонент, соответствую­щих спектру модулирующих частот, и устранения компонент, соот­ветствующих спектру несущего колебания и его гармоник. Таким обра­зом, функциональная схема детектора может быть представлена в виде последовательно соединенных нелинейного элемента и фильтра нижних частот. В качестве нелинейных элементов используют полупро­водниковые диоды, а также биполярные и полевые транзисторы. Роль фильтра, как правило, выполняет цепь, состоящая из резистора и шун­тирующей его емкости. В настоящее время элементы детектора чаще реализуют в одной микросхеме.

На рис. 4.1 показана схема последовательного амплитудного де­тектора, а на рис. 4.2 - параллельного детектора.

Схема параллельного амплитудного детектора дополнена фильтром нижних частот .

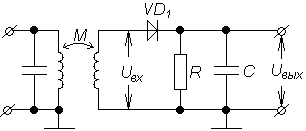
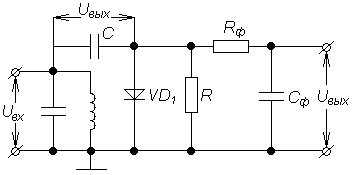
Рис. 4.1. АД последовательного Рис. 4.2. АД параллельного

типа. типа.

Постоянная времени детектора выбирается в соответствии с неравенством:

---

Смотрите также файлы

• Развитие у дошкольников чувства сопричастности к миру взрослых через форимрование представлений о мире.docx

• зіді тексер 1 Ахмет Байтрсынлы кім.docx

• fashion world Масаты.pptx

• Б отырысында аралды Мектеп директоры.docx

• Четверть 2 Предмет.doc