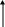(1 / f₀) << RC << (1 / f_м). (4.1)
Левая часть этого неравенства характеризует способность детектора отфильтровывать высокочастотные составляющие детектируемого сигнала, а правая часть отображает требование воспроизведения формы низкочастотного модулирующего колебания.
В данной работе в качестве нелинейного элемента используется диод. Исследуемая схема последовательного детектора может работать в двух различных режимах, которые определяются выбором положения рабочей точки на ВАХ диода.

В первом случае рабочая точка выбирается на нижнем изгибе ВАХ, что соответствует детектированию слабых сигналов. Поскольку начальный участок ВАХ диода хорошо аппроксимируется полиномом второй степени, то такой режим детектирования называется квадратичным.

Во втором случае производится детектирование сильных сигналов. При этом используется линейный участок ВАХ диода и режим детектирования называется линейным.

При квадратичном режиме коэффициент гармоник К_г = М / 4, т.е. прямо пропорционален коэффициенту модуляции М.
Порядок выполнения работы
1. Собрать схему 4.1, моделирующую работу амплитудного детектора.


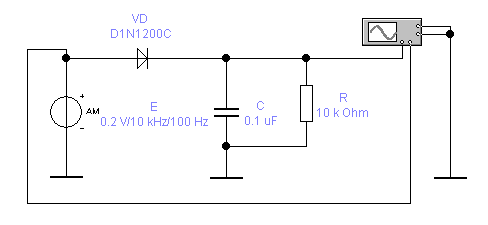
Схема 4.1.
2. Для моделирования режима квадратичного детектирования установить параметры элементов:

2.1. Генератор АМ-колебаний (AМ source) Е:

- амплитуда сигнала VC = 0.1 В;

- несущая частота (FC) f₀ = 10N кГц;

- модулирующая частота (FM) f_м = 100N Гц;

- коэффициент модуляции М = 0.3.

2.2. Диод VD взять типа D1N1200C (из библиотеки программы в меню “Models”, “motorol1”).

2.3. Сопротивление R = 10 кОм.

2.4. Конденсатор С выбрать из двойного неравенства (4.1).

3. Перенести осциллограмму полученного колебания (с учётом постоянной составляющей сигнала) в отчёт.

4. С помощью пунктов меню “Analysis” → “Fourier” получить спектральную диаграмму на выходе схемы. Для этого перед началом спектрального анализа в меню “Fourier” установить:

- номер точки выходного узла схемы в окне “Output node” (заранее определяется так: подвести курсор к выходному узлу схемы, нажать правую кнопку мышки, войти в меню “Component properties”, в открывшемся окне “Node ID” прочитать номер узла);

- в окне “Fundamental frequency” - шаг частоты для анализа, равный частоте модулирующего сигнала f

---

_м;

- число гармоник “Number harmonics” равное 15.

5. Перенести спектрограмму в отчёт. Записать полученный коэффициент нелинейных искажений (Total harmonic distortion).

6. Повторить п.п. 3 - 5 для значений коэффициента модуляции М = 0.5, 0.8 и 1.0.

7. Результаты свести в таблицу.

М	Кг квадр , %	Кг линей , %
0,3
0,5
0,8
1,0

8. Проанализировать полученные результаты.
9. Для моделирования режима линейного детектирования увеличить амплитуду генератора АМ-колебаний Е до 1 В.
10. Повторить п.п. 3 – 8.

Содержание отчёта
1. Исследуемые схемы.

2. Результаты вычислений и измерений.

3. Формы сигналов.

4. Графики полученных диаграмм.

5. Результаты проведенного анализа и выводы по работе.


Контрольные вопросы
1. Что такое демодуляция (детектирование) сигнала?

2. Каков принцип детектирования АМ-колебаний?

3. Что такое квадратичный режим детектирования АМ-колебаний?

4. Что такое линейный режим детектирования АМ-колебаний?

5. Какие недостатки и преимущества квадратичного режима детектирования?

6. Какие недостатки и преимущества линейного режима детектирования?

7. Поясните результаты измерений, сведённые в таблицу пункта 7.

8. Поясните критерий выбора постоянной времени RC цепи для линейного режима детектирования.

9. Как в дальнейшем устранить постоянную составляющую сигнала на выходе АД?

ЛАБОРАТОРНАЯ РАБОТА № 5
Частотно-модулированные колебания
Цель работы: изучить и проанализировать характеристики частотно-модулированных (ЧМ) колебаний.
Общие положения
В методе частотной модуляции (ЧМ) амплитуда модулирующего сигнала управляет мгновенной частотой несущей. Идеальная ЧМ не вносит изменений в амплитуду несущей. Следовательно, форма напряжения модулированной несущей может быть выражена в виде

е_чм=А_нcos[_нt+sin(_мt)],

где _н и _м - соответственно несущая частота и частота модуля­ции, а  - индекс модуляции. Частоты модулированного колеба­ния могут быть получены из выражения cos[_нt+sin(_м

---

t)] с ис­пользованием тригонометрических формул и специальных таблиц (функции Бесселя).

Индекс модуляции  определяется как _н/_м=f_н/f_м - от­ношение максимальной девиации частоты (за один период модули­рующего сигнала) к частоте модуляции.

Амплитуда спектральных составляющих ЧМ колебания определяется величиной индекса частотной модуляции. При узкополосной ЧМ (<<1) амплитудный спектр ЧМ колебания совпадает со спектром АМ колебания. При больших индексах модуляции (>>1) ширина спектра ЧМ колебания близка к удвоенной девиации частоты.

Существуют различные методы ЧМ-детектирования и селекции. В основе большинства методов лежит использование наклона час­тотной характеристики резонансного контура (рис. 5.1). Амплитуда отклика изменяется с частотой. Для _н+_н получаем амплиту­ду А₁, для _н-_н - амплитуду А_2, а для частот между _н+_н и _н-_н имеем все промежуточные амплитуды меж­ду А₁ и А₂. Выходной сигнал соответствует девиации частоты вход­ного сигнала (хотя и не совсем линейно в простом резонансном кон­туре) и тем самым воспроизводит первоначальный модулирующий сигнал.

В частотном детекторе с расстроенным колебательным контуром (схема 5.2) осуществляется предварительное преобразование изменений частоты радиосигнала в пропорциональное изменение амплитуды. Последующее детектирование этого преобразованного радиосигнала осуществляется с помощью обычного детектора АМ колебаний.



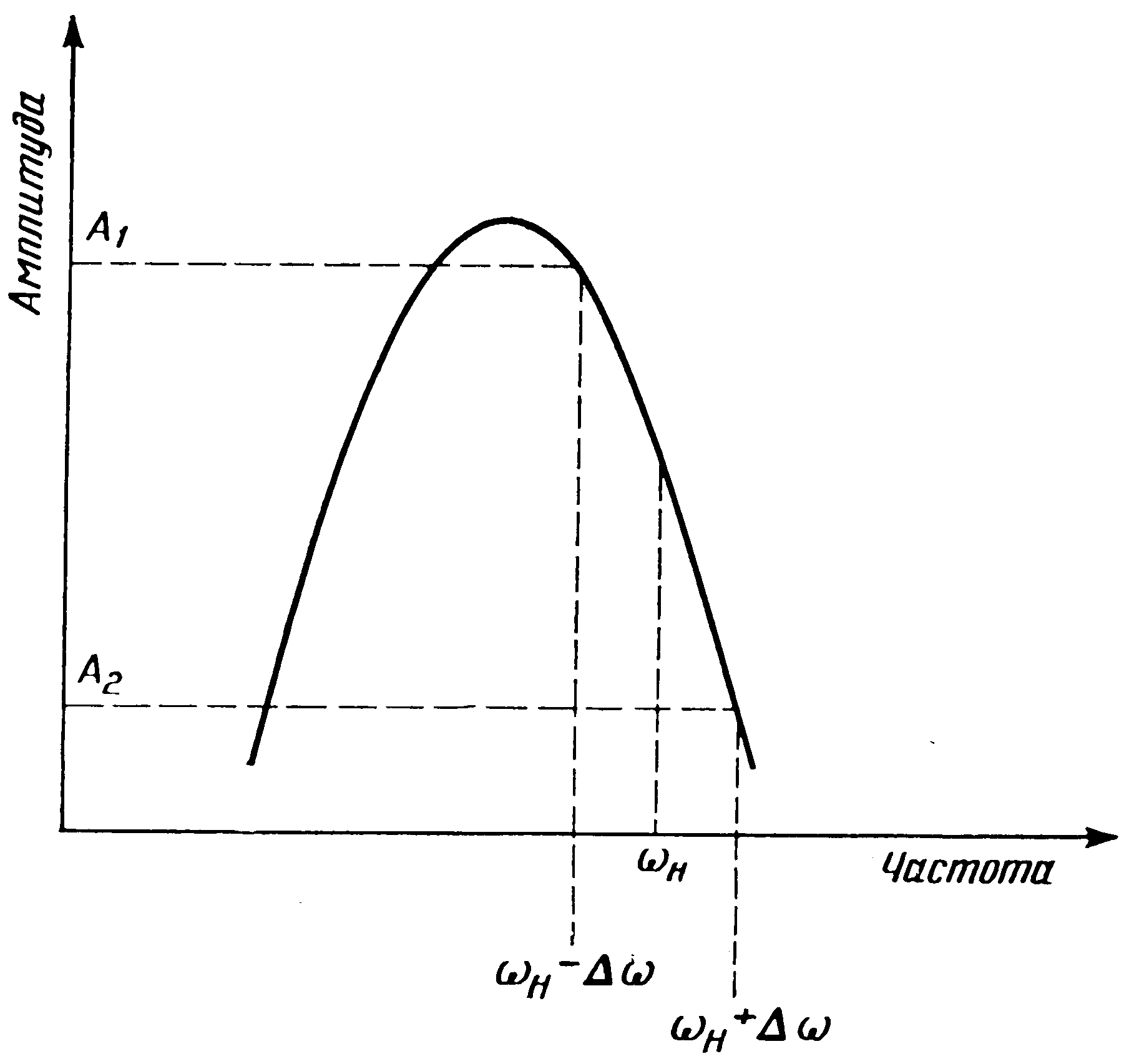
Рис. 5.1. Принцип использования резонансного контура в качестве частот­ного детектора.

Порядок выполнения работы
1. Собрать схему 5.1 для исследования ЧМ колебания.


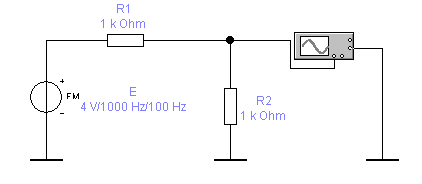
Схема 5.1.
2. Установить параметры элементов:

2.1. Генератор ЧМ-колебаний (FМ source) Е:

- амплитуда сигнала VC = 20 / N, В;

- несущая частота FC = 1 кГц;

- модулирующая частота FM = 100 Гц;

- индекс модуляции М = 5.

2.2. Сопротивления R1 и R2 по 1 кОм каждый.

3. Перенести осциллограмму полученного колебания в отчёт.

4. С помощью пунктов меню “Analysis” → “Fourier” получить спектральную диаграмму на выходе схемы. Для этого перед началом спектрального анализа в меню “Fourier” установить:

- шаг частоты для анализа, равный частоте модулирующего сигнала (в нашем случае – 100 Гц) в окне “Fundamental frequency”;

---

- число гармоник “Number harmonics” равное 21.

5. Перенести спектрограмму в отчёт.

6. Получить и зафиксировать в отчёте спектрограммы для значений индекса модуляции М, равным 2.0, 1.0 и 0.5.

7. Проанализировать полученные результаты.

8. Собрать схему 5.2, моделирующую процесс демодуляции ЧМ сигнала с помощью расстроенного колебательного контура.



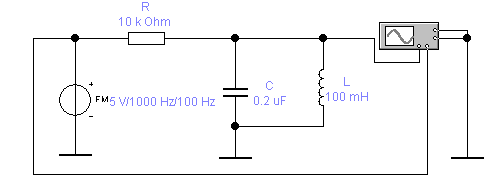
Схема 5.2.
9. Установить параметры элементов:

9.1. Генератор ЧМ-колебаний (FМ source) Е:

- амплитуда сигнала VC = 20 / N, В;

- несущая частота FC = 1 кГц;

- модулирующая частота FM = 100 Гц;

- индекс модуляции М = 0.1.

12.2. Сопротивление R = 10 кОм.

12.3. Индуктивность L = 0.1 Гн.

12.4. Величину ёмкости С рассчитать так, чтобы колебательный контур был настроен на частоту 1100 Гц. Расчёт отобразить в отчёте.

13. Снять и перенести в отчёт осциллограмму полученного выходного напряжения.

14. Повторить п. 13 для значений индекса модуляции М, равным 0.3 и 0.5.

15. Проанализировать полученные результаты.

16. Заменив в схеме 5.2 источник АМ сигнала Е на генератор синусоидального напряжения, снять и перенести в отчёт АЧХ и ФЧХ схемы в диапазоне частот от 500 до 1500 Гц. Убедиться в правильности расчёта резонансной частоты LC контура.
Содержание отчёта
1. Исследуемые схемы.

2. Результаты вычислений и измерений.

3. Формы сигналов.

4. Графики полученных диаграмм.

5. Результаты проведенного анализа и выводы по работе.

Контрольные вопросы
1. Что такое угловая модуляция? Какие виды колебаний с угловой модуляцией Вы знаете?

2. Какой спектр имеет ЧМ-колебание? От чего он зависит?

3. Что общего между ЧМ и ФМ колебаниями?

4. В чём разница между ЧМ и ФМ колебаниями?

5. Какие недостатки ФМ колебания?

6. Каков принцип демодуляции ЧМ колебаний детектором с расстроенным колебательным контуром?

7. Что такое частотная манипуляция?

8. Что такое индекс модуляции? Каков его физический смысл?

9. Что происходит со спектром ЧМ-колебания при М >> 1?

10. Что такое добротность колебательного контура? Как её рассчитать и каков её физический смысл?

11. Какая добротность колебательного контура должна быть в схеме 5.2? Почему?

12. Что такое девиация частоты?

ЛАБОРАТОРНАЯ РАБОТА № 6
Умножение и преобразование частоты сигнала
Цель работы: изучить и проанализировать принципы и процессы преобразования частоты (переноса спектра) сигналов.

---

Общие положения
Если на нелинейный элемент (базу транзистора) подать входной сигнал большой величины, то можно получить ток коллектора в виде последовательности остроконечных импульсов. Такой ток богат гармониками, образующими линейчатый спектр. В составе импульсного коллекторного тока будут присутствовать гармоники с частотами, кратными основной частоте возбуждения. Это позволяет использовать усилитель в качестве умножителя частоты. Для этого достаточно настроить нагрузочный колебательный контур на частоту выделяемой гармоники и установить режим работы нелинейного элемента, наиболее выгодный для подчёркивания полезной гармоники. Оптимальный угол отсечки можно рассчитывать по соотношению θ_опт = 120°/ n, где n – порядок умножения частоты.

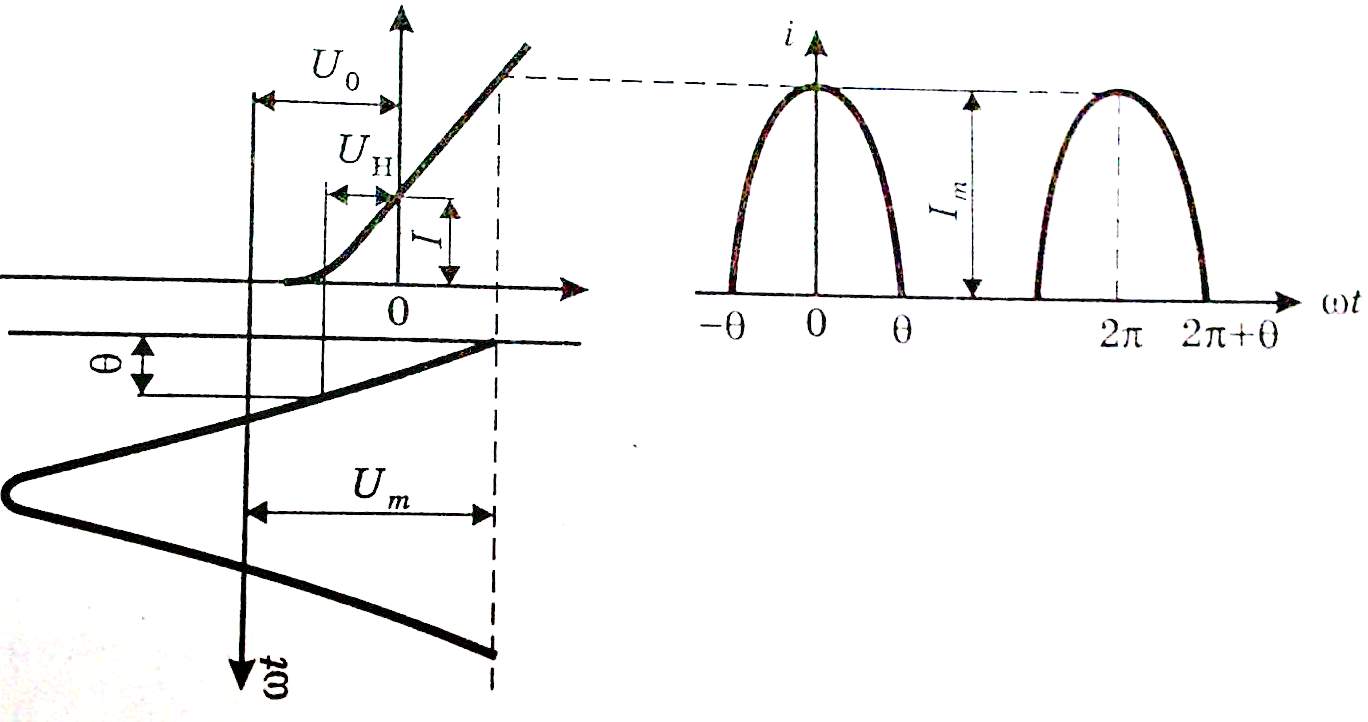
Напряжение смещения U₀ определяется из формулы:

,

где: S – крутизна проходной характеристики транзистора, U_m – амплитуда входного сигнала, U_н – напряжение запирания активного элемента, I – ордината точки пересечения аппроксимирующей прямой с осью ординат.

Процесс преобразования частотного спектра, при котором в выходной цепи выделяется комбинационная частота (разностная или суммарная), называется преобразованием частоты. Преобразование частоты осуществляется с помощью нелинейных элементов.

Преобразователем частоты называют устройство, осуществляющее перенос спектра радиосигнала из одной области частот в другую. Так как сигнал несет в себе полезную информацию, заключенную в одном или нескольких его параметрах, то в процессе преобразования частоты эта информация должна сохраняться. Естественно, что в реальных условиях всегда имеют место искажения информации, которые не должны превосходить некоторых допустимых значений.

Этим условиям наиболее полно соответствует принцип гетеродинного преобразования частоты:

НЭ

ИС
f_c f_пр

---

Смотрите также файлы

• Развитие у дошкольников чувства сопричастности к миру взрослых через форимрование представлений о мире.docx

• зіді тексер 1 Ахмет Байтрсынлы кім.docx

• fashion world Масаты.pptx

• Б отырысында аралды Мектеп директоры.docx

• Четверть 2 Предмет.doc