Файл: Линейная алгебра и аналитическая геометрия на плоскости.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.03.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение
высшего образования
«Северный (Арктический) федеральный университет имени М.В. Ломоносова»
Высшая школа энергетики, нефти и газа
_____________________________________________________
(наименование высшей школы / филиала / института / колледжа)
КОНТРОЛЬНАЯ РАБОТА
| По дисциплине/междисциплинарному курсу/модулю | Высшая математика | |
| | ||
| | ||
| На тему | Линейная алгебра и аналитическая геометрия на плоскости. Пределы последовательностей и функций. Вариант 8 | |
| | ||
| | Выполнил (-а) обучающийся (-аяся): Заболотский Юрий Иванович |
| | (Ф.И.О.) |
| | Направление подготовки / специальность: Теплоэнергетика теплотехника |
| | (код и наименование) |
| | Курс: 1 |
| | Группа: 113205 |
| | Руководитель: Попов Василий Николаевич, профессор |
| | (Ф.И.О. руководителя, должность / уч. степень / звание) |
| Отметка о зачете | | | | |
| | | (отметка прописью) | | (дата) |
| Руководитель | | | | |
| | | (подпись руководителя) | | (инициалы, фамилия) |
Архангельск 2022
Задание 1
а) Вычислите матрицу А; б) найдите матрицу, обратную к матрице А.
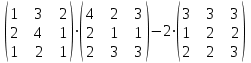
Решение
Матрица А
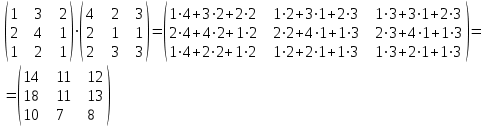
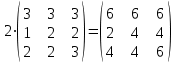
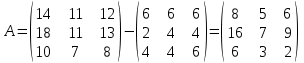
Обратная матрица
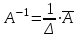
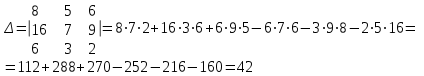
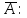
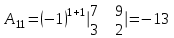
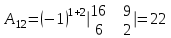
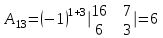
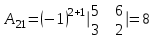
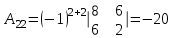
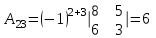
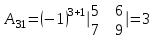
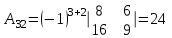
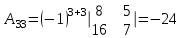
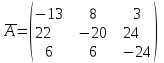
Обратная матрица
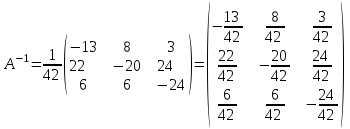
Проверка
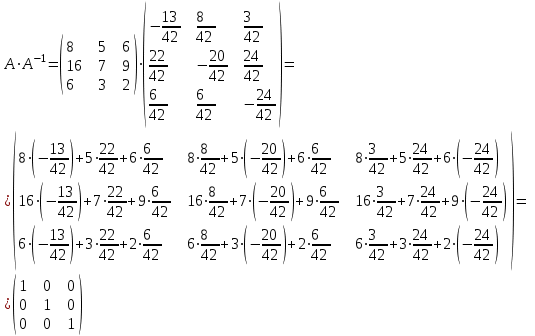
Ответ.
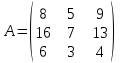 ,
, 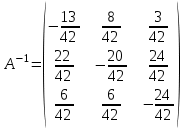
Задание 2
Решите систему линейных уравнений методом Гаусса, Крамера и обратной матрицы
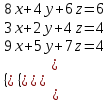
Решение
Метод Гаусса
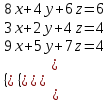
Элементы 1-й строки, умноженные на -3, складываем с элементами 2-й строки, умноженными на 8, и результат записываем во 2-ю строку; элементы 1-й строки, умноженные на -9, складываем с элементами 3-й строки, умноженными на 8, и результат записываем в 3-ю строку; значения элементов 1-й строки не меняем
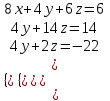
Элементы 2-й строки, умноженные на -1, складываем с элементами 3-й строки, и результат записываем в 3-ю строку; значения элементов 2-й строки не меняем
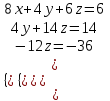
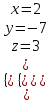
Метод Крамера
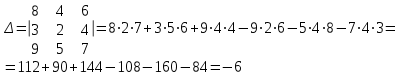
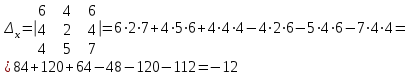
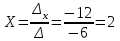
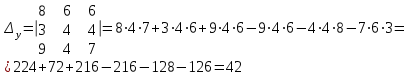
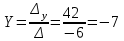
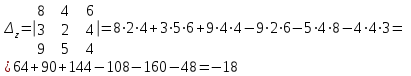
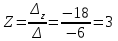
Метод обратной матрицы
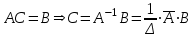
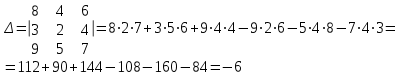
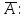
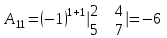
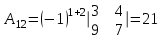
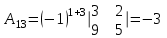
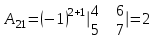
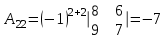
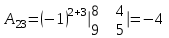
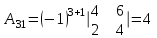
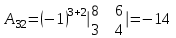
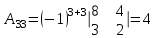
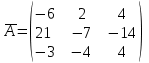
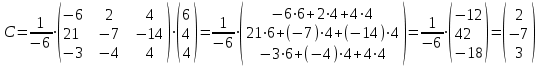
Проверка
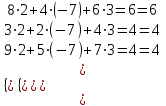
Ответ.
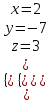
Задание 3
Даны точки на плоскости А (3, 4), В (7, 7), С (2, 6).
-
a) Найдите уравнения прямой АВ (параметрическое, каноническое, общее, с угловым коэффициентом, в отрезках). -
b) Найдите длину отрезка АВ. -
c) Найдите уравнение прямой, перпендикулярной прямой АВ и проходящей через точку С. -
d) Найдите уравнение прямой, параллельной прямой АВ и проходящей через точку С. -
e) Найдите длину перпендикуляра, опущенного на прямую АВ из точки С. -
f) Найдите косинус угла АСВ. -
g) Найдите площадь треугольника АВС.
Постройте все найденные прямые, а также сам треугольник АВС, на одном чертеже.
Решение:
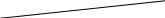






С
В
А
-
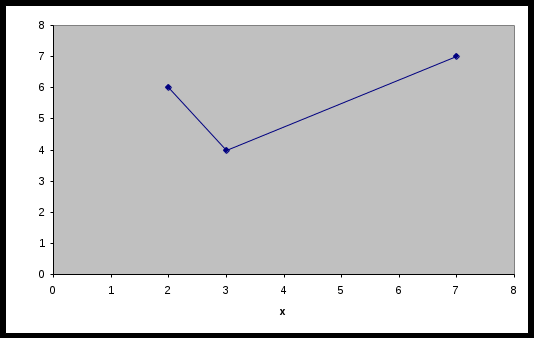
a) Уравнения прямой АВ (параметрическое, каноническое, общее, с угловым коэффициентом, в отрезках). -
Параметрическое уравнение прямой
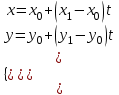
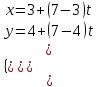
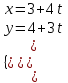
Каноническое уравнение прямой
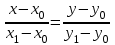
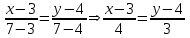
Общее уравнение прямой
Уравнение, прямой проходящей через две точки
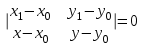
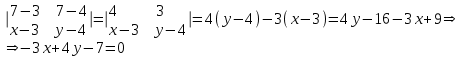
Уравнение прямой с угловым коэффициентом
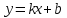
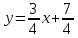
Уравнение прямой в отрезках
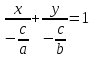
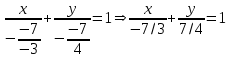
b) Длина отрезка АВ
Расстояние между двумя точками
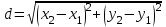
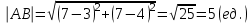
c) Уравнение прямой, перпендикулярной прямой АВ и проходящей через точку С
Уравнение прямой, проходящей через точку перпендикулярно другой прямой
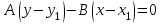
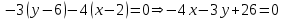
d) Уравнение прямой, параллельной прямой АВ и проходящей через точку С
Уравнение прямой, проходящей через точку параллельно другой прямой
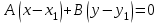
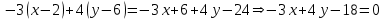
e) Длина перпендикуляра, опущенного на прямую АВ из точки С
Расстояние от точки до прямой
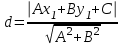
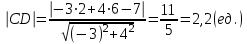
f) Косинус угла АСВ
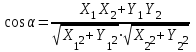
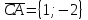
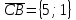
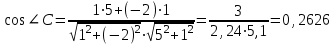
g) Площадь треугольника АВС
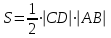
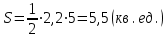
А (3, 4), В (7, 7), С (2, 6).
Ответ. а)
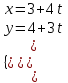 ,
, 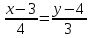 ,
, 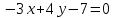 ,
,  ,
, 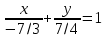
b)
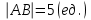 , с)
, с) 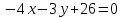 , d)
, d) 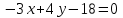 , е)
, е) 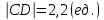 ,
, f)
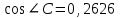 , g)
, g) 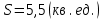
Задание 4
Дана кривая второго порядка.
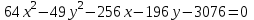
a) Приведите кривую второго порядка к каноническому виду.
b) Найдите эксцентриситет кривой.
c) Найдите уравнения директрис.
d) Найдите координаты фокусов кривой.
e) Найдите уравнения асимптот (для гиперболы).
f) Постройте кривую второго порядка, фокусы и директрисы на одном чертеже.
