ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Урок
Тема: «Построение сечений тетраэдра и параллелепипеда».
Предмет: геометрия
Класс: 10
Используемые педагогические технологии:
технология проектного обучения, информационные технологии.
Тема урока: Построение сечений тетраэдра и параллелепипеда
Тип урока: урок закрепления и развития знаний.
Формы работы на уроке: фронтальная, индивидуальная
Список используемых источников и программно-педагогических средств:
-
Л.С. Атанасян. Геометрия. 10-11 классы,- М: Просвещение, 2014г. -
Программное обеспечение динамической математики GeoGebra.
Цели:
Образовательные:
Проверить знание теоретического материала о многогранниках (тетраэдр, параллелепипед).
Продолжить формирование умения анализировать чертеж, выделять главные элементы при работе с моделью многогранника, намечать ход решения задачи, предвидеть конечный результат.
Отработать навыки решения задач на построение сечений многогранников.
Развивать графическую культуру и математическую речь.
Формировать навыки использования компьютерных технологий на уроках геометрии.
Развивающие:
Развивать познавательный интерес учащихся.
Формировать и развивать у учащихся пространственное воображение.
Воспитательные:
Воспитывать самостоятельность, аккуратность, трудолюбие.
Воспитывать умения работать индивидуально над задачей.
Воспитывать волю и настойчивость для достижения конечных результатов.
Техническое обеспечение:
Компьютерный класс, программное обеспечение динамической математики GeoGebra, мультимедиапроектор.
Раздаточный материал:
Бланки-карточки с заданиями для практической работы, бланки-карточки с ответами.
Структура урока.
| 1. | Приветствие. Организационный момент. | 1 мин |
| 2. | Постановка цели и задачи урока. | 2 мин |
| 3. | Повторение изученного материала. | 5 мин |
| 4. | Изучение нового материала. | 12мин |
| 5. | Практическая работа на построение сечений. | 15мин |
| 6. | Проверка выполнения работы. | 5 мин |
| 7. | Домашнее задание | 2 мин |
| 8. | Рефлексия. | 2 мин |
| 9. | Итоги | 1 мин |
Ход урока:
1)Приветствие. Организационный момент.
2) Постановка цели и задачи урока.
- Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений является основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью.
На предыдущих уроках мы с вами рассмотрели алгоритмы построения несложных сечений куба, тетраэдра и параллелепипеда. Эти сечения, как правило, задавались точками, расположенными на ребрах или гранях многогранника. Сегодня на уроке мы с вами научимся строить сечения тетраэдра и параллелепипеда плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани. Для этого мы будем использовать программу GeoGebra.
3) Повторение изученного материала.
- Давайте повторим некоторые вопросы теории.
-
Что такое секущая плоскость? -
Как можно задать секущую плоскость? -
Что такое сечение тетраэдра (параллелепипеда)? -
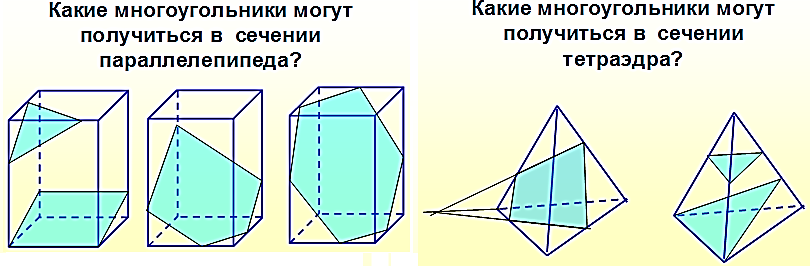
Какие многоугольники мы получали при построении сечений тетраэдра? -
А какие многоугольники мы можем получить при построении сечений параллелепипеда?
4) Изучение нового материала
Изучение темы «Решение задач на построение сечений» облегчается с помощью различных компьютерных программ. Одной из таких программ является программное обеспечение динамической математики GeoGebra. Она подходит для изучения и обучения на любом из этапов образования, облегчает создание математических построений и моделей обучающимися, которые позволяют проводить интерактивные исследования при перемещении объектов и изменение параметров.
Рассмотрим применение этого программного продукта на конкретном примере.
Задача 1
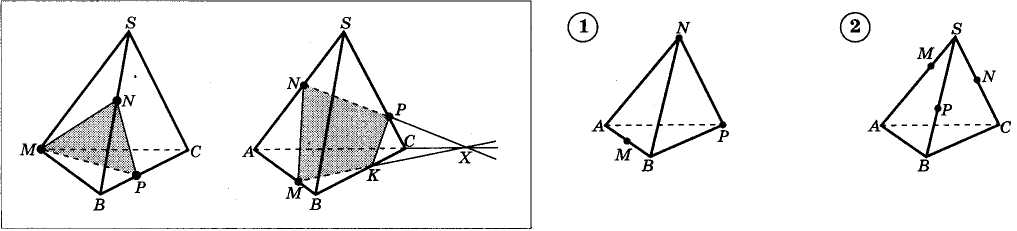
На ребрах AB, BC, CD тетраэдра DABC отмечены точки M, N, P (рис. 1). Построить сечение тетраэдра плоскостью MNP.
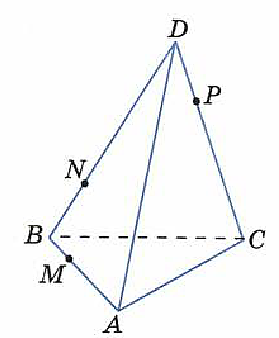

рис. 1
-
Откроем программу GeoGebra. -
В меню Вид выберем Полотно 3D (Полотно 2D можно закрыть) -
С помощью инструмента создадим тетраэдр DABC.
создадим тетраэдр DABC. -
С помощью инструмента на ребрах AB, BC, CD тетраэдра DABC отметим точки M, N, P (переименовать точку можно выделив ее и вызывая контекстное меню правой кнопкой мыши, выбрать соответствующий пункт).
на ребрах AB, BC, CD тетраэдра DABC отметим точки M, N, P (переименовать точку можно выделив ее и вызывая контекстное меню правой кнопкой мыши, выбрать соответствующий пункт). -
Построим прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E (рис. 2), которая и будет второй общей точкой плоскостей MNP и ABC Для этого выбрав инструмент нужно щелкнуть поочерёдно по точкам N, P и B, C и с помощью инструмента
нужно щелкнуть поочерёдно по точкам N, P и B, C и с помощью инструмента  отметить точку E – точку пересечения прямых NP и BC.
отметить точку E – точку пересечения прямых NP и BC.

рис. 2
Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро AC в некоторой точке Q.

-
Проведём прямую ME выбрав инструмент и щелкнув поочерёдно по точкам M, E. С помощью инструмента
и щелкнув поочерёдно по точкам M, E. С помощью инструмента  отметим точку Q – точку пересечения прямой ME и ребра AC.
отметим точку Q – точку пересечения прямой ME и ребра AC. -
Четырёхугольник МNPQ – искомое сечение. Выделим его используя инструмент поочерёдно щелкая по точками M, N, P, Q, M.
поочерёдно щелкая по точками M, N, P, Q, M.
рис. 3
-
Д важды щелкнув по объектам Tetrahedron и Четырёхугольник (рис. 3) можно вызвать контекстное меню с настройками, в которых можно выбрать цвет заливки и прозрачность соответствующего объекта.
важды щелкнув по объектам Tetrahedron и Четырёхугольник (рис. 3) можно вызвать контекстное меню с настройками, в которых можно выбрать цвет заливки и прозрачность соответствующего объекта.

Также при построении сечений необходим инструмент
Задача 2.
 На ребрах параллелепипеда даны три точки A, B, C. Построить сечение параллелепипеда плоскостью ABC (рис. 4).
На ребрах параллелепипеда даны три точки A, B, C. Построить сечение параллелепипеда плоскостью ABC (рис. 4).
рис. 4
При построении сечений параллелепипеда следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны. Для создания параллелепипеда требуется использовать инструмент
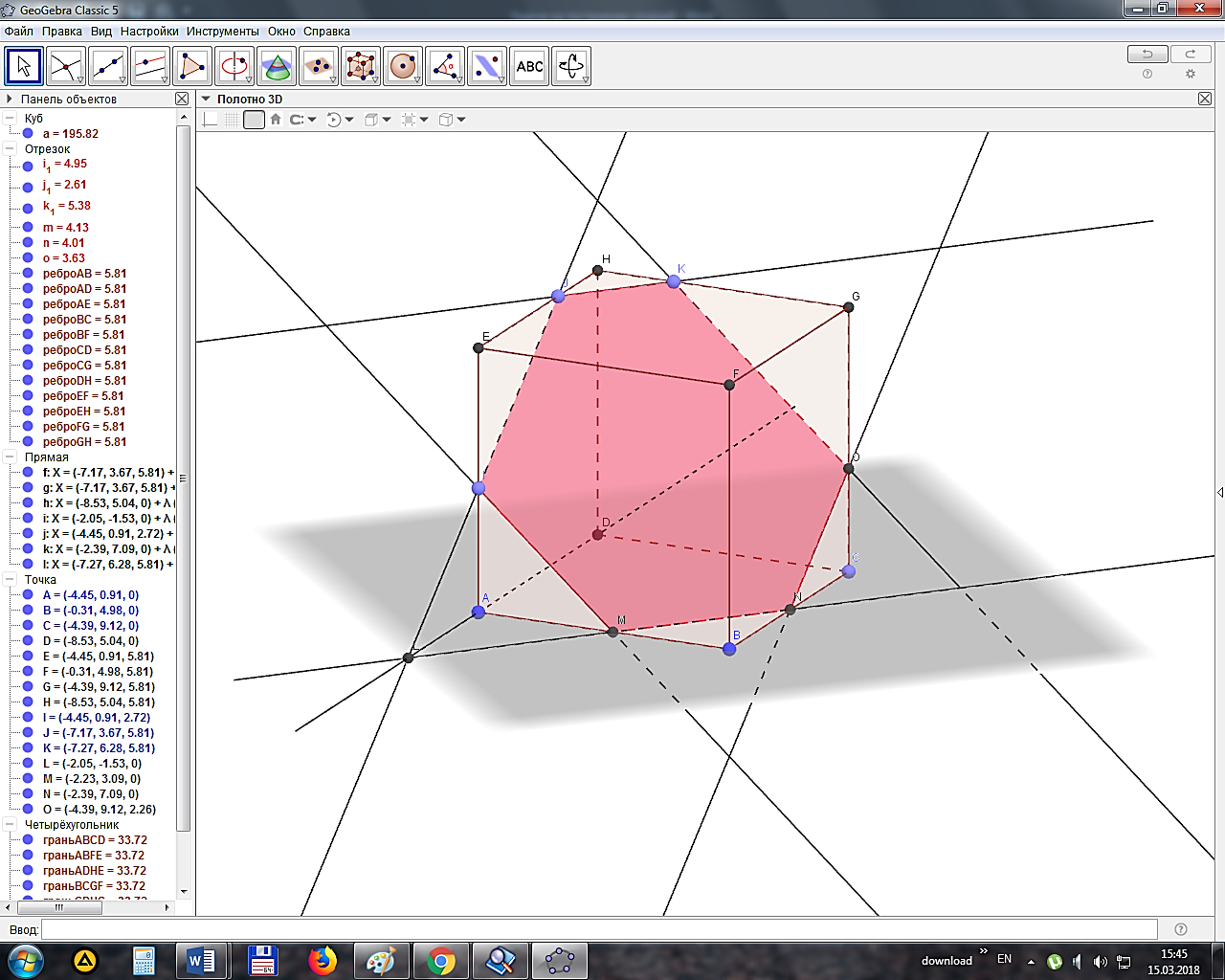
5) Практическая работа в программной среде GeoGebra на построение сечений.
Ученики получают бланки-карточки для практической работы (приложение 1, приложение 2) и садятся за компьютеры для выполнения практической работы. На бланках также расположено несколько различных примеров построения сечений. Практическая работа состоит из 12 вариантов по 2 задания на построение сечений тетраэдра и параллелепипеда. Учитель контролирует выполнение работы и помогает учащимся в случае затруднений.
6) Проверка выполнения работы.
Ученики получают бланки с ответами (приложение 3). Проверяют работы друг друга, отмечая правильно построенные сечения. Учитель оценивает работы учащихся.
7) Домашнее задание.
- В качестве домашнего задания я попрошу вас решить задачи, аналогичные задачам в практической работе. Каждому предлагается выбрать 2 других варианта заданий.
8) Рефлексия.
- Итак, подведем итог, чему мы научились сегодня на уроке?
- Какие теоретические положения нам часто приходилось использовать?
- Какие ошибки были допущены при решении задач? Как вы их устранили?
- Кому приходилось возвращаться к задаче несколько раз?
- Где в практической деятельности вам пригодится сегодняшний урок?
На этапе рефлексии деятельности учащиеся анализируют, где и почему были допущены ошибки, каким способом они были исправлены, повторяют алгоритмы, вызвавшие затруднения, оценивают свою деятельность на уроке.
9) Итог урока.
В завершение урока учащиеся с помощью учителя фиксируют степень соответствия поставленной цели и результатов деятельности. Выставляются оценки.
Практическая работа по построению сечений параллелепипеда. Приложение 1
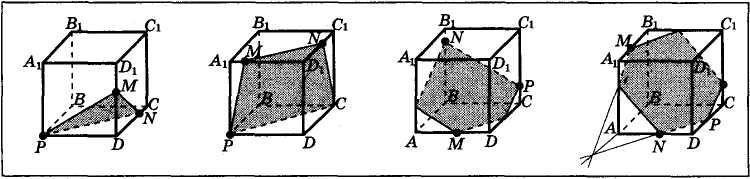


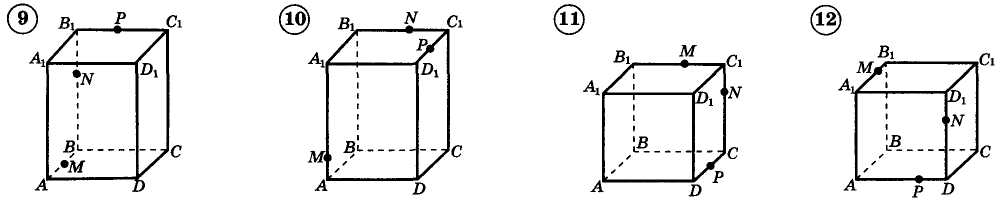
Приложение 3
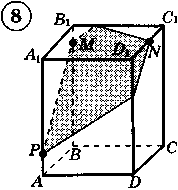
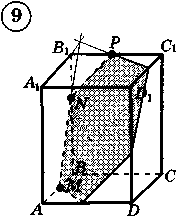
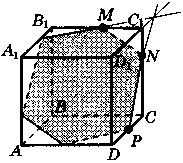
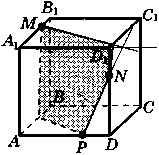
Ответы к практической работе.
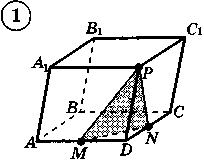 | 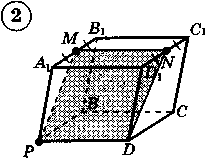 | 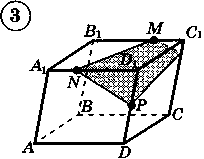 | 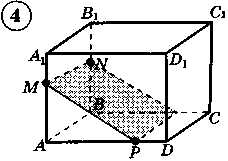 |
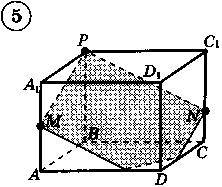 | 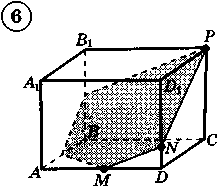 |  |  |
 |  |  |  |
Приложение 2