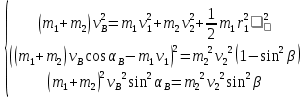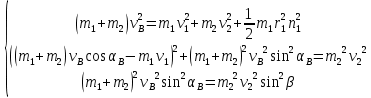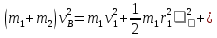ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ В РОССИИ



ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики

Расчетно-графическое задание

По дисциплине физика

Вариант: 4

Автор: студент гр. САМ-22 __________ Скуковский П. А.
подпись (Ф.И.О.)

ОЦЕНКА: ______________

Дата: ___________________

ПРОВЕРИЛ: доцент Силиванов М.О. .

должность подпись (Ф.И.О.)

Санкт-Петербург

2022 год

Краткое теоретическое содержание:
Твердым телом называют систему материальных точек, взаимное расположение которых не будет меняться ни при каких обстоятельствах (между любыми двумя точками расстояние постоянно).
Любое сложное движение твердого тела можно представить как комбинацию поступательного и вращательного движения.
Поступательным называется такое движение, при котором любая прямая, мысленно проведенная в теле, остается постоянной самой себе в течение всего времени движения. При поступательном движении траектории всех точек тела одинаковы, скорости и ускорения всех точек в данный момент времени равны. Поэтому можно описывать движение одной точки.
Вращательным называют такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, а плоскости перпендикулярны к ней.
Траектория — линия, описываемая в пространстве движущейся точкой. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.
Скорость - векторная величина, характеризующая быстроту движения и его направление в данный момент времени.

---

Мгновенная скорость — векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, в течение которого это перемещение произошло.



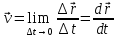
Мгновенная скорость v, таким образом, есть векторная величина, определяемая первой производной радиуса-вектора движущейся точки по времени.

Модуль мгновенной скорости равен первой производной пути по времени:



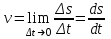
Единица скорости [м/с].
Ускорение – векторная величина, характеризующая быстроту изменения скорости как по модулю, так и по направлению со временем.
Ускорение, 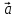есть векторная величина, определяемая первой производной скорости по времени.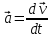


Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих


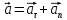
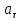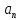Тангенциальная составляющая ускорения характеризует быстроту изменения модуля скорости (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту изменения направления скорости (направлена по главной нормали к центру кривизны траектории). Составляющие и перпендикулярны друг другу.

Момент инерции тела – относительно данной оси называется физическая величина, равная сумме произведений элементарных масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.


Момент инерции тела 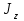является мерой инертности тела во вращательном движении вокруг неподвижной оси 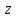подобно тому, как масса тела является мерой его инертности в поступательном движении.
Момент инерции для цилиндра равен

,

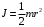где 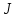– момент инерции тела, m – масса тела, r – расстояние до некоторой оси.

Сумму кинетической и потенциальной энергий называют полной механической энергией

---

Е.

Закон сохранения энергии: в замкнутой системе, в которой действуют только консервативные силы, полная энергия остаётся неизменной.



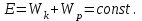
Закон сохранения импульса для замкнутой системы материальных точек - суммарный импульс замкнутой системы материальных точек остаётся постоянным

Задание:

Самолет летит на высоте 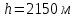со скоростью 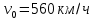под углом 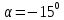к горизонту. В некоторый момент времени он выпускает в направлении своего полета снаряд, который спустя время 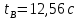взрывается.


В результате взрыва снаряда образуются два осколка массо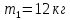й и 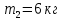. При этом первый осколок летит по параболической траектории, имея начальную скорость 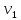, направленную горизонтально поверхности земли. В результате разрыва данный осколок приобрел угловую скорость вращения 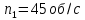вдоль своей продольной оси. Второй осколок, имея скорость 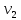, также летит по параболической траектории под некоторым углом к горизонту .


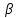Считая первый осколок цилиндром массой 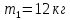и радиусом 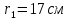, найти суммарную энергию, которая выделится при его падении на землю.

Определить скорости осколков 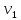и 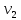сразу после взрыва, а также угол 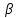, под которым полетит второй осколок к горизонту.

Построить графики зависимости скорости второго осколка от времени 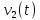, тангенциальной составляющей ускорения снаряда от времени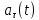

---

и траектории снаряда .

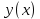Дано:

























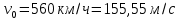
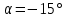
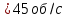
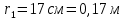
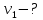
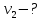
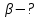
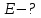
Решение:

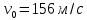Считаем, что самолет выпускает снаряд на высоте со скоростью под углом к горизонту относительно Земли.

Так, на снаряд, выпущенный под углом к горизонту, действует только сила тяжести (в отсутствии сопротивления воздуха), направленная вертикально вниз, то по оси y движения тела равнопеременное с ускорением свободного падения, направленным вниз, а по оси x движения равномерное.

Проекция скорости на ось х:

.

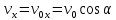Поскольку по условию 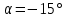, следовательно, снаряд начинает лететь ускоренно, со скоростью, относительно оси у: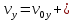



где 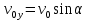- проекция начальной скорости на ось у.

В момент времени 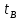проекция его скорости, на ось у будет равна: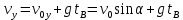



Полная скорость в момент взрыва снаряда равна

---

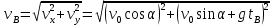
И направлена под углом 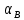к горизонту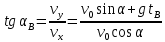





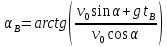
И будет находиться на высоте



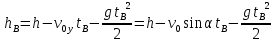
Подставляем числовые значения







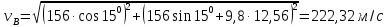
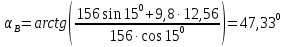
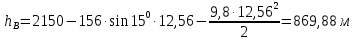
Схематически траектория движения изображается в виде параболы.

Запишем законы сохранения энергии и импульса для снаряда до и после взрыва.

Закон сохранения кинетической энергии, с учетом, что первый осколок начинает вращаться:



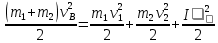
где момент инерции первого осколка (цилиндра)



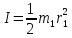
Тогда имеем



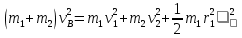
закон сохранения импульса в векторной форме





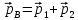
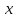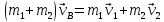
Проекции на координатные оси:





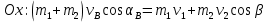
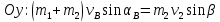
Получили систему уравнений с тремя неизвестными:



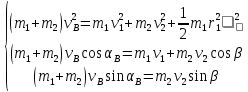
Решая данную систему, находим 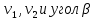. Преобразуем систему, заменив 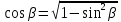, и возведем в квадрат второе и третье уравнения:

---

Смотрите также файлы

• Тема Модель Школа Минпросвещения России.pdf

• Решение Наиболее полно финансовая устойчивость предприятия может быть раскрыта на основе изучения равновесия между статьями актива и пассива баланса..doc

• Морепродукты блюдо питание.docx

• Сегодня на уроке.pptx

• LOMoARcpsd.docx