Файл: Составить план производства продукции, обеспечив максимум прибыли, учитывая ограничения.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 19.03.2024

Просмотров: 21

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления
Форма обучения: заочная


ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Моделирование экономических процессов

Группа Бк18Э171

Студент
Н.Ю. Матвеева

МОСКВА2020

Практические занятия




№ 1. Составить план производства продукции, обеспечив максимум прибыли, учитывая ограничения.



Исходные данные представлены в таблице 1.

Таблица 1. Линейная оптимизация
Расход сырья (доли)
Прибыль от реализации единицы продукции, руб.

Сырье 1
Сырье 2
Сырье 3
Сырье 4

Продукт 1
0,2
0,3
0,1
0,4
120

Продукт 2
0,4
0,1
0,3
0,2
150

Продукт 3
0,6
0,1
0,1
0,2
110

Наличие сырья на складе, кг
850
640
730
1000



Решение:

Пусть 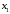, , 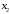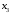– искомые объемы производства продукции. Ограничения имеют вид: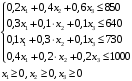



Суммарная прибыль от продажи продукции должна быть максимальной:

.

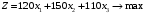Экономико-математическую модель задачи:



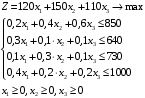
Найдем значения переменных , которые удовлетворяют системе ограничений и дают максимальное значение целевой функции.

Для упрощения вычислений умножим систему ограничений на 10. Получим:



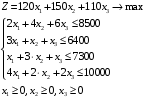
Решим исходную задачу симплексным методам. Приведем модель к каноническому виду: введем дополнительные переменные 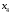, , 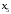, , 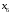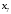означающие остатки ресурсов.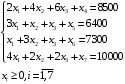



Преобразуем целевую функцию – перенесем правую часть влево:



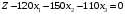
В качестве базисных переменных выбираем 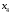, ,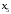 , 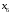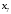. Строим первую симплексную таблицу (начальный опорный план).

Базисные переменные
Базисные координаты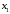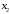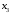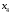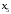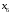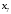














Симплексные отношения



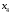8500
2
4
6
1
0
0
0





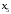6400
3
1
1
0
1
0
0





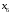7300
1
3
1
0
0
1
0





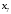10000
4
2
2
0
0
0
1





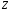0
–120
–150
–110
0
0
0
0



Опорный план определяется столбцами базисных переменных и базисных координат): , , , , , , . .

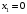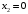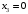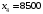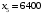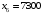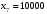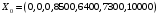Построенный опорный план X0 не является оптимальным, так как в строке целевой функции есть отрицательные элементы. Необходимо перейти к новому базису и построить новый опорный план.

Из всех отрицательных элементов в строке целевой функции выбираем наименьший -150. Столбец, в котором находится этот элемент, называется разрешающим. Вычислим симплексные отношения. Из всех симплексных отношений выбираем наименьшее, и соответствующую строку назовем разрешающей. На пересечении разрешающего столбца и разрешающей строки получаем разрешающий элемент. Получим:

Базисные переменные
Базисные координаты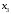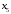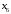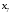














Симплексные отношения



8500
2
4
6
1
0
0
0
8500/4=2125



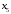6400
3
1
1
0
1
0
0
6400/1=6400



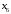7300
1
3
1
0
0
1
0
7300/32433



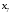10000
4
2
2
0
0
0
1
10000/2=5000



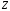0
–120
–150
–110
0
0
0
0



Строим новый опорный план, т. е. составляем новую симплексную таблицу. Переменная, стоящая в разрешающем столбце, переходит в базис (вместо x4 пишем x2). Заполняем столбцы базисных переменных: на месте разрешающего элемента делаем 1, выше и ниже нули, получим:

Базисные переменные
Базисные координаты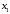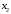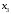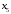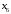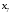














Симплексные отношения



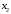2125
½
1
3/2
¼
0
0
0





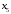4275
5/2
0
-1/2
-1/4
1
0
0





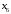925
-1/2
0
-7/2
-3/4
0
1
0





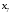5750
3
0
-1
-1/2
0
0
1





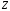318750
–45
0
115
75/2
0
0
0



Данный план не является оптимальным, так как в
последней строке есть отрицательный элемент, строим новый опорный план.

Базисные переменные
Базисные координаты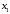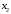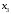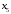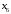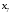














Симплексные отношения



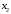2125
1/2
1
3/2
¼
0
0
0
2125/0,5=4250



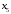4275
5/2
0
-1/2
-1/4
1
0
0
4275/2,5=1710



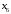925
-1/2
0
-7/2
-3/4
0
1
0
-



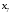5750
3
0
-1
-1/2
0
0
1
5750/31917



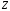318750
–45
0
115
75/2
0
0
0


Смотрите также файлы