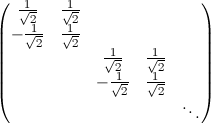ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 6
Скачиваний: 0
Вейвлет-сжатие
Ве́йвлет (англ. wavelet — небольшая волна, рябь), иногда, гораздо реже[1], вэйвлет — математическая функция, позволяющая анализировать различные частотные компоненты данных.
Вейвлетное сжатие — общее название класса методов кодирования изображений, использующих двумерное вейвлет-разложение кодируемого изображения или его частей. Обычно подразумевается сжатие с потерей качества.
Сжатие изображений
Упрощённо, изображение представляют собой таблицу, в ячейках которой хранятся цвета каждого пикселя. часто значения яркости берут целыми из диапазона от 0 до 255. Тогда каждое значение будет занимать ровно 1 байт. Плохая новость в том, что для изображения этот теоретический предел сжатия не так уж и велик. Это происходит из-за того, что в изображениях из реального мира (фотографиях, например) значения яркости редко бывают одинаковыми даже у соседних пикселей. Всегда есть мельчайшие колебания, которые неуловимы человеческим глазом, но которые алгоритм сжатия честно пытается учесть. Алгоритмы сжатия «любят», когда в данных есть закономерность. Лучше всего сжимаются длинные последовательности нулей (закономерность тут очевидна). В самом деле, вместо того, чтобы записывать в память 100 нулей, можно записать просто число 100 (конечно, с пометкой, что это именно количество нулей). Декодирующая программа «поймёт», что имелись в виду нули и воспроизведёт их. Однако если в нашей последовательности в середине вдруг окажется единица, то одним числом 100 ограничится не удастся. Но зачем кодировать абсолютно все детали? Ведь когда мы смотрим на фотографию, нам важен общий рисунок, а незначительные колебания яркости мы и не заметим. А значит, при кодировании мы можем немного изменить изображение так, чтобы оно хорошо кодировалось. При этом степень сжатия сразу вырастет. Правда, декодированное изображение будет незначительно отличаться от исходного, но кто заметит?
Вейвлетная компрессия в современных алгоритмах компрессии изображений позволяет значительно (до двух раз). повысить степень сжатия чёрно-белых и цветных изображений при сравнимом визуальном качестве по отношению к алгоритмам предыдущего поколения, основанным на дискретном косинусном преобразовании, таких, например, как JPEG.
Преобразование Хаара
У «реальных» изображений, таких как фотографии, есть одна особенность — яркость соседних пикселей обычно отличается на небольшую величину. В самом деле, в мире редко можно увидеть резкие, контрастные перепады яркости. А если они и есть, то занимают лишь малую часть изображения.
Рассмотрим
фрагмент первой строки яркостей из
известного изображения
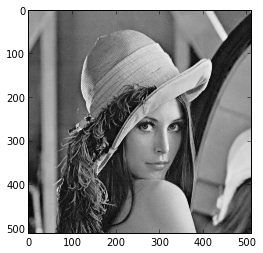
154, 155, 156, 157, 157, 157, 158, 156
Видно, что соседние числа очень близки. Чтобы получить желаемые нули или хотя бы что-то близкое к ним, можно закодировать отдельно первое число, а потом рассматривать лишь отличия каждого числа от предыдущего. Получаем:
154, 1, 1, 1, 0, 0, 1, -2.
Такой метод в самом деле используется и называется дельта-кодированием. Но у него есть серьёзные недостаток — он нелокальный. То есть нельзя взять кусочек последовательности и узнать, какие именно яркости в нём закодированы без декодирования всех значений перед этим кусочком. Попробуем поступить иначе. Не будем пытаться сразу получить хорошую последовательность, попробуем улучшить её хотя бы немного. Для этого разобьём все числа на пары и найдём полусуммы и полуразности значений в каждой из них. (154, 155), (156, 157), (157, 157), (158, 156)
(154.5, 0.5), (156.5, 0.5), (157, 0.0), (157, -1.0)
Почему именно полусуммы и полуразности? А всё очень просто! Полусумма — это среднее значение яркости пары пикселей. А полуразность несёт в себе информацию об отличиях между значениями в паре. Очевидно, зная полусумму a и полуразность d можно найти и сами значения: первое значение в паре = a — d, второе значение в паре = a + d. Это преобразование было предложено в 1909 году Альфредом Хааром и носит его имя. А где же сжатие?
Если разделить полусуммы и полуразности: 154.5, 156.5, 157, 157; 0.5, 0.5, 0.0, -1.0.
Числа
во второй половине последовательности
как правило будут небольшими
Как
мы уже выяснили раньше, в реальных
изображениях соседние пиксели редко
отличаются друг от друга значительно..
Если
рассмотрим первые 2000 пар соседних
пикселей и каждую пару представим на
графике точкой.
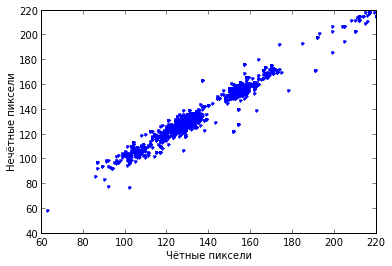 Все
точки выстраиваются вдоль одной прямой
линии. И так практически во всех реальных
изображениях. Верхний левый и нижний
правый углы изображения практически
всегда пусты.
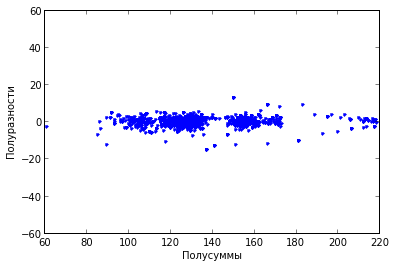
А
теперь рассмотрим график, точками в
котором будут полусуммы и
полуразности.
Все
точки выстраиваются вдоль одной прямой
линии. И так практически во всех реальных
изображениях. Верхний левый и нижний
правый углы изображения практически
всегда пусты.
А
теперь рассмотрим график, точками в
котором будут полусуммы и
полуразности.
 Видно,
что полуразности находятся в гораздо
более узком диапазоне значений. А это
значит, что на них можно потратить меньше
одного байта. Какое-никакое, а
сжатие.
Применим
математику!
Видно,
что полуразности находятся в гораздо
более узком диапазоне значений. А это
значит, что на них можно потратить меньше
одного байта. Какое-никакое, а
сжатие.
Применим
математику!
Попробуем
записать математические выражения,
описывающие преобразование Хаара.
Итак,
у нас была пара пикселей (вектор) ![]() ,
а мы хотим получить пару
,
а мы хотим получить пару ![]() .
Такое
преобразование описывается матрицей
.
Такое
преобразование описывается матрицей ![]() .
В
самом деле
.
В
самом деле ![]() ,
что нам и требовалось.
Если
обратить внимание на графики, то можна
заметить что рисунки из точек на двух
последних графиках одинаковы. Разница
лишь в повороте на угол в 45°.
В
математике повороты и растяжения
называются аффинными преобразованиями
и описываются как раз при помощи умножения
матрицы на вектор. Что мы и получили
выше. То есть, преобразование Хаара —
это просто поворот точек таким образом,
чтобы их можно было удобно и компактно
закодировать.
Правда,
тут есть один нюанс. При аффинных
преобразованиях может меняться площадь
фигуры. Не то, чтобы это было плохо, но
как-то неаккуратненько. Как известно,
коэффициент изменения площади равен
определителю матрицы. Посмотрим, каков
он для преобразования Хаара.
,
что нам и требовалось.
Если
обратить внимание на графики, то можна
заметить что рисунки из точек на двух
последних графиках одинаковы. Разница
лишь в повороте на угол в 45°.
В
математике повороты и растяжения
называются аффинными преобразованиями
и описываются как раз при помощи умножения
матрицы на вектор. Что мы и получили
выше. То есть, преобразование Хаара —
это просто поворот точек таким образом,
чтобы их можно было удобно и компактно
закодировать.
Правда,
тут есть один нюанс. При аффинных
преобразованиях может меняться площадь
фигуры. Не то, чтобы это было плохо, но
как-то неаккуратненько. Как известно,
коэффициент изменения площади равен
определителю матрицы. Посмотрим, каков
он для преобразования Хаара.
![]() Для
того, чтобы определитель стал равен
единице достаточно умножить каждый
элемент матрицы на
Для
того, чтобы определитель стал равен
единице достаточно умножить каждый
элемент матрицы на ![]() .
На угол поворота (а значит, и на «сжимающую
способность» преобразования) это не
повлияет.
Получаем
в итоге матрицу
.
На угол поворота (а значит, и на «сжимающую
способность» преобразования) это не
повлияет.
Получаем
в итоге матрицу
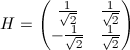 Увеличиваем
число точек
Увеличиваем
число точек
Всё
сказанное хорошо работает для двух
точек. Но что делать, если точек больше?
В
этом случае тоже можно описать
преобразование матрицей, но большей по
размеру. Диагональ этой матрицы будет
состоять из матриц H, таким образом в
векторе исходных значений будут
выбираться пары, к которым независимо
будет применяться преобразование
Хаара.
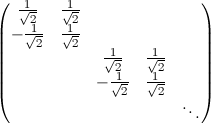 То
есть. исходный вектор просто обрабатывается
независимо по парам.
Фильтры
То
есть. исходный вектор просто обрабатывается
независимо по парам.
Фильтры
Итак,
когда мы знаем, как выполнять преобразование
Хаара, попробуем разобраться с тем, что
же оно нам даёт.
Полученные
«полусуммы» (из-за того, что делим не на
2, приходится использовать кавычки) —
это, как мы уже выяснили, средние значения
в парах пикселей. То есть, фактически,
значения полусумм — это уменьшенная
копия исходного изображения! Уменьшенная
потому, что полусумм в два раза меньше,
чем исходных пикселей.
Но
что такое разности?
Полусуммы
усредняют значения яркостей, то есть
«отфильтровывают» случайные всплески
значений. Можно считать, что это некоторый
частотный фильтр.
Аналогично,
разности «выделяют» среди значений
межпиксельные «всплески» и устраняют
константную составляющую. То есть, они
«отфильтровывают» низкие частоты.
Таким
образом, преобразование Хаара — это
пара фильтров, разделяющих сигнал на
низкочастотную и высокочастотную
составляющие. Чтобы получить исходный
сигнал, нужно просто снова объединить
эти составляющие.
Что
нам это даёт? Пусть у нас есть
фотография-портрет. Низкочастотная
составляющая несёт в себе информацию
об общей форме лица, о плавных перепадах
яркости. Высокочастотная — это шум и
мелкие детали.
Обычно,
когда мы смотрим на портрет, нас больше
интересует низкочастотная составляющая,
а значит при сжатии часть высокочастотных
данных можно отбросить. Тем более, что,
как мы выяснили, она обычно имеет меньшие
значения, а значит более компактно
кодируется.
Степень
сжатия можно увеличить, применяя
преобразование Хаара многократно. В
самом деле, высокочастотная составляющая
— это всего лишь половина от всего
набора чисел. Но что мешает применить
нашу процедуру ещё раз к низкочастотным
данным? После повторного применения,
высокачастотная информация будет
занимать уже 75%.
этот
подход хорошо применим и для двумерных
данных. Чтобы выполнить двумерное
преобразование Хаара (или аналогичное
ему), нужно лишь выполнить его для каждой
строки и для каждого столбца.
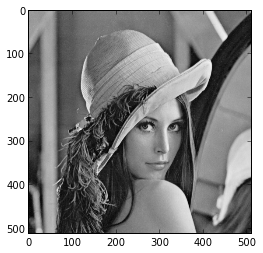
После
многократного применения к, например,
фотографии замка Лихтенштейн, получим
следующий рисунок.
 Черные
области соответствуют низкой яркости,
то есть значениям, близким к нулю. Как
показывает практика, если значение
достаточно мало, то его можно округлить
или вообще обнулить без особого ущерба
для декодированного рисунка.
Этот
процесс называется квантованием. И
именно на этом этапе происходит потеря
части информации. (К слову, такой же
подход используется в JPEG, только там
вместо преобразования Хаара используется
дискретное косинус-преобразование.)
Меняя число обнуляемых коэффициентов,
можно регулировать степень сжатия!
Конечно,
если обнулить слишком много, то искажения
станут видны на глаз. Во всём нужна
мера!
После
всех этих действий у нас останется
матрица, содержащая много нулей. Её
можно записать построчно в файл и сжать
каким-то архиватором. Например, тем же
7Z. Результат будет неплох.
Декодирование
производится в обратном порядке:
распаковывем архив, применяем обратное
преобразование Хаара и записываем
декодированную картинку в файл.
Черные
области соответствуют низкой яркости,
то есть значениям, близким к нулю. Как
показывает практика, если значение
достаточно мало, то его можно округлить
или вообще обнулить без особого ущерба
для декодированного рисунка.
Этот
процесс называется квантованием. И
именно на этом этапе происходит потеря
части информации. (К слову, такой же
подход используется в JPEG, только там
вместо преобразования Хаара используется
дискретное косинус-преобразование.)
Меняя число обнуляемых коэффициентов,
можно регулировать степень сжатия!
Конечно,
если обнулить слишком много, то искажения
станут видны на глаз. Во всём нужна
мера!
После
всех этих действий у нас останется
матрица, содержащая много нулей. Её
можно записать построчно в файл и сжать
каким-то архиватором. Например, тем же
7Z. Результат будет неплох.
Декодирование
производится в обратном порядке:
распаковывем архив, применяем обратное
преобразование Хаара и записываем
декодированную картинку в файл.
154, 155, 156, 157, 157, 157, 158, 156
154, 1, 1, 1, 0, 0, 1, -2.
______________
(154, 155), (156, 157), (157, 157), (158, 156)
(154.5, 0.5), (156.5, 0.5), (157, 0.0), (157, -1.0)
154.5, 156.5, 157, 157; 0.5, 0.5, 0.0, -1.0.

Итак,
у нас была пара пикселей (вектор) 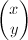 ,
а мы хотим получить пару
,
а мы хотим получить пару 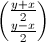 .
Такое
преобразование описывается матрицей
.
Такое
преобразование описывается матрицей  .
В
самом деле
.
В
самом деле 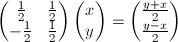 ,
что нам и требовалось.
,
что нам и требовалось.
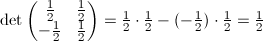

______________________