Числа и векторы

Тема 1. Действительные числа

Развитие понятия числа

Наиболее общие закономерности и законы экономических явлений выясняются путем качественного анализа, но конкретное выражение их возможно лишь с помощью меры и числа.



Число — важнейшее математическое понятие, меняющееся на протяжении веков.

Первые представления о числе возникли из счета людей, животных, плодов, различных изделий и пр. Результатом являются натуральные числа: 1, 2, 3, 4, ...

При счете отдельных предметов единица есть наименьшее число и делить ее на доли не нужно, а иногда и нельзя, однако уже при грубых измерениях величин приходится делить 1 на доли. Исторически первым расширением понятия числа является присоединение к натуральному числу дробных чисел.

Дробью называется часть (доля) единицы или несколько равных ее частей.

Обозначаются:   где m и n — целые числа;   — сокращение дроби;   — расширение. Дроби со знаменателем 10n , где n — целое число, называются десятичными:   

Среди десятичных дробей особое место занимают периодические дроби:   — чистая периодическая дробь,   — смешанная периодическая дробь.

Дальнейшее расширение понятия числа вызвано уже развитием самой математики (алгебры). Декарт в XVII в. вводит понятие отрицательного числа.

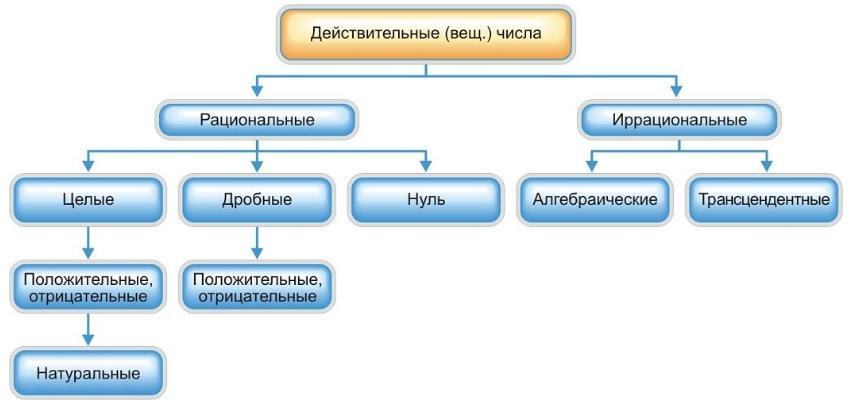
Числа целые (положительные и отрицательные), дробные (положительные и отрицательные) и нуль получили название рациональных чисел. Всякое рациональное число может быть записано в виде дроби конечной и периодической.

Для изучения непрерывно изменяющихся переменных величин оказалось необходимым новое расширение понятия числа — введение действительных (вещественных) чисел — присоединением к рациональным числам иррациональных: 

---

иррациональные числа — это бесконечные десятичные непериодические дроби.

Иррациональные числа появились при измерении несоизмеримых отрезков (сторона и диагональ квадрата), в алгебре — при извлечении корней   примером трансцендентного, иррационального числа являются 

Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — 
Режим доступа к курсу: http://e-college.ru. — П. 2.1.

Числа натуральные (1, 2, 3, ...), целые (..., –3, –2, –1, 0, 1, 2, 3, ...), рациональные (представимые в виде m / n, где m и n ≠ 0 — целые числа) и иррациональные (не представимые в виде m / n) образуют множество действительных (вещественных) чисел.

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 24.

Все действительные числа можно изобразить на числовой оси. Числовая ось (числовая прямая):

а) горизонтальная прямая с выбранным на ней направлением;

б) начало отсчета — точка 0;

в) единица масштаба.



Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. — 
Режим доступа к курсу: http://e-college.ru. — П. 2.1.

Свойства действительных чисел

1. 
   a + b = b + a.
   
2. 
   а + (b + с) = (а + b) + с.
   
3. 
   а + 0 = а.
   
4. 
   а + (–а) = 0.
   
5. 
   ab = b а.
   
6. 
   a (bc) = (ab) с.
   
7. 
   а · 0 = 0.
   
8. 
   а · 1 = a.
   
9. 
   
   
10. 
    a (b + c) = ab + ac .
    

Комплексные числа возникают в связи с задачей решения квадратных и других алгебраических уравнений.

Комплексным числомназывается выражение вида z = x + iy , где x и y — действительные числа, i - мнимая единица. Число x называется действительной частью

---

, а y - мнимой частью числа z (обозначаются соответственно x = Re (z), y = Im (z)).

Действительное число x является частным случаем комплексного числа z = x + iy при y = 0. Если y ≠ 0, то комплексные числа вида z = x + iy называются мнимыми, а при x = 0, y ≠ 0, т.е. числа вида z = iy , — чисто мнимыми.

Числа z = x + iy и z = x – iy называются комплексно-сопряженными.

Два комплексных числа z₁ = x₁ + i y₁ и z₂ = x₂ + i y₂ pавны, если x₁ = x₂, y₁ = y₂. Число z = 0, если x = 0, y = 0.

Отношений «больше», «меньше» для комплексных чисел не существует.

Цит. по: Математика для экономистов: от Арифметики до Эконометрики:
учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. —
М.: Высшее образование, 2009. — (Основы наук) — С. 25.



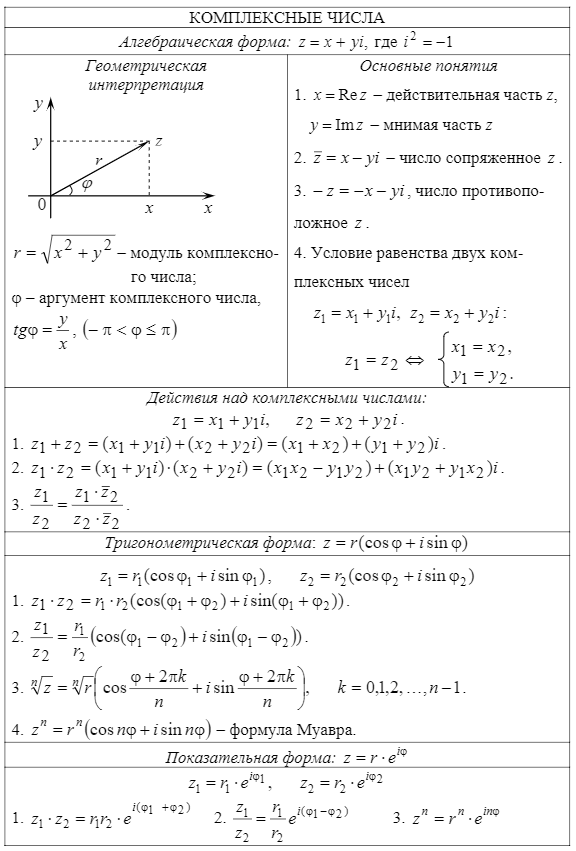
Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 46.

Степенью   с натуральным показателем n называется произведение n одинаковых сомножителей, равных 



где   — основание степени; n — показатель степени.

В частности, 1ⁿ = 1; 0ⁿ = 0 (n ≠ 0).

По определению



Правила действий со степенями (а ≥ 0, b > 0, с ≥ 0) (2.2).

1. 
   (abc)ⁿ = aⁿ bⁿ cⁿ;
   
2. 
   a^m × aⁿ = a^m + n;
   
3. 
   (a^m)ⁿ = a^mn;
   
4. 
   
   
5. 
   
   

---

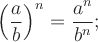
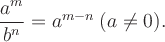
Основные алгебраические формулы:

а² – b² = (а – b) (а + b); 

(а ± b)³ = а³ ± 3а²b + 3а b² ± b³;

(а ± b)² = a² ± 2ab + b² ;

a³ ± b³ = (а ± b) (a² ± ab + b²); (2.3)

(а + b + ... + k + l)² = а² + b² + ... + k² + l² + 2 (ab + ... + ak + al + bc +...+ bk + bl + ... + kl);

aⁿ – bⁿ = (a – b)(a^n–1 + a^n–2 b + a^n–3 b² + ... + a b^n–2+ b^n–1).

(Например, (a + b + c)² = a² + b² + c² + 2 (ab + ac + bc); a⁵ – b⁵ = (a – b) (a⁴ + a³b + a²b² + ab³ + b⁴).

Корнем степени n из числа а называется число, n-я степень которого равна заданному числу 

 (2.4)

где   — подкоренное выражение; n — показатель корня (n ∈ N).

(Например,   так как 3⁵ = 243.)

По определению

 (2.4′)

Действие нахождения корня называется извлечением корня.

Арифметическим корнем, или арифметическим значением корня, n-й степени называется неотрицательное число   (n -я степень которого равна а). (Например,   — арифметические,    — неарифметические корни.) На множестве действительных чисел под корнем 

---

четной степени (n = 2k) из неотрицательного числа подразумевается его арифметическое значение (например,   а не –3). (На множестве комплексных чисел   имеет n значений.)

Выражения, содержащие знак корня (радикал), называются иррациональными.

Правила действий с корнями (а ≥ 0, b > 0, с ≥ 0; n ≥ 2, p ≥ 2 (n, m ∈ N)):



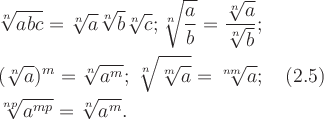
(Например,



Указанные правила безоговорочно верны для арифметических корней.

(Например,



а не



Для четного n = 2k.



т.е.



(например,



так как





так как



По определению степень с рациональным (дробным) показателем



где   m ∈ M , n ∈ N.

(Например,



Для степеней с дробным показателем сохраняются те же правила действий со степенями (2.2), приведенные выше.

Формула сложного радикала

---

Смотрите также файлы

• .rtf

• Соловьев Вл. Философские начала цельного знания В. Соловьев. Сочинения. В 2 т. М. 1988. Т. С. 179 181, 227 229.docx

• Искусство звука.docx

• Тест Кожа Вариант 1 Выберите один правильный ответ Загар образуется при.docx

• Латекс фагоцитозына тест анытайды Нейтрофильдерді жту асиетін.docx