1. Преобразование Фурье.

Преобразование Фурье (символ ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами (подобно тому, как музыкальный аккорд может быть выражен в виде амплитуд нот, которые его составляют ).

Преобразование Фурье функции {\displaystyle f}вещественной переменной является интегральным и задаётся следующей формулой:

Операция преобразования Фурье математически записывается следующим образом:

где  - символ прямого преобразования Фурье.

Спектры в теории автоматического управления представляют графически, изображая отдельно их действительную и мнимую части:

На рис. 1 представлено типичное изображение спектра непериодического сигнала.

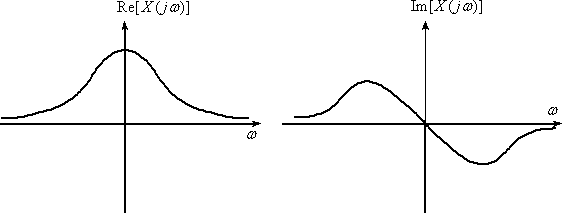
Рис. 1

Отметим следующие особенности спектра непериодической функции :

1. Спектр непериодической функции времени непрерывен;

2. Область допустимых значений аргумента спектра

3. Действительная часть спектра – четная функция частоты, мнимая часть спектра – нечетная функция, что позволяет использовать одну половину спектра

Преобразование Фурье обратимо, то есть, зная Фурье-изображение, можно определить исходную функцию – оригинал. Соотношение обратного преобразования Фурье имеет следующий вид:

---

или в сокращенной записи , где  - символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:

• функция однозначна, содержит конечное число максимумов, минимумов и разрывов;

• функция абсолютно интегрируема, то есть

Обратное преобразование Фурье возможно только в том случае, если все полюсы  - левые.

Рассмотрим примеры определения спектра временных функций.

Пример:

Найдем частотный спектр дельта-функции.

,

так как при 

,

а при   и

.

В итоге,  имеет единичный, равномерный и не зависящий от частоты действительный спектр, а мнимая часть спектра будет равна нулю (см. рис.2).

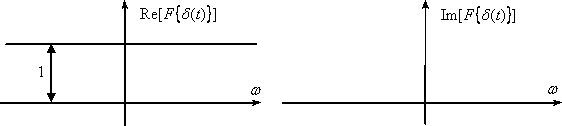
Рис. 2

2. Кривые Безье.

Кривые Безье используются в компьютерной графике для рисования плавных изгибов, в CSS-анимации и много где ещё. В принципе, можно создавать анимацию и без знания кривых Безье, но стоит один раз изучить эту тему хотя бы для того, чтобы в дальнейшем с комфортом пользоваться этим замечательным инструментом. Тем более что в мире векторной графики и продвинутых анимаций без них никак.

Виды кривых Безье:

Кривая Безье задаётся опорными точками. Их может быть две, три, четыре или больше. Например:

По двум точкам:

---

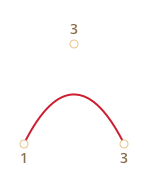
По трём точкам:

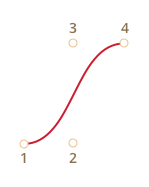
По четырём точкам:

Если вы посмотрите внимательно на эти кривые, то «на глазок» заметите:

---

1. Точки не всегда на кривой. Это совершенно нормально, как именно строится кривая мы рассмотрим чуть позже.

2. Степень кривой равна числу точек минус один. Для двух точек – это линейная кривая (т.е. прямая), для трёх точек – квадратическая кривая (парабола), для четырёх – кубическая.

3. Кривая всегда находится внутри выпуклой оболочки, образованной опорными точками:

Благодаря последнему свойству в компьютерной графике можно оптимизировать проверку пересечений двух кривых. Если их выпуклые оболочки не пересекаются, то и кривые тоже не пересекутся.

Основная ценность кривых Безье для рисования – в том, что, двигая точки, кривую можно менять, причём кривая при этом меняется интуитивно понятным образом.

Математика

У кривых Безье есть математическая формула.

Координаты кривой описываются в зависимости от параметра t⋲[0,1]

• Для двух точек:

P = (1-t)P₁ + tP₂

• Для трёх точек:

P = (1−t)²P₁ + 2(1−t)tP₂ + t²P₃

• Для четырёх точек:

• P = (1−t)³P₁ + 3(1−t)²tP₂ +3(1−t)t²P₃ + t³P₄

• Вместо P_i нужно подставить координаты i-й опорной точки (x_i, y_i).

• Эти уравнения векторные, то есть для каждой из координат:

• x = (1−t)²x₁ + 2(1−t)tx₂ + t²x₃

• y = (1−t)²y₁ + 2(1−t)ty₂ + t²y₃

• Вместо x₁, y₁, x₂, y₂, x₃, y₃ подставляются координаты трёх опорных точек, и в то время как t пробегает множество от 0 до 1, соответствующие значения (x, y) как раз и образуют кривую.

• Итого

• Кривые Безье задаются опорными точками.

• Мы рассмотрели два определения кривых:

1. Через математическую формулу.

2. Через процесс построения де Кастельжо.

• Их удобство в том, что:

• Можно легко нарисовать плавные линии вручную, передвигая точки мышкой.

• Более сложные изгибы и линии можно составить, если соединить несколько кривых Безье.

• Применение:

• В компьютерной графике, моделировании, в графических редакторах. Шрифты описываются с помощью кривых Безье.

• В веб-разработке – для графики на Canvas или в формате SVG. Кстати, все живые примеры выше написаны на SVG. Фактически, это один SVG-документ, к которому точки передаются параметрами. Вы можете открыть его в

---

• отдельном окне и посмотреть исходник: demo.svg.

• В CSS-анимации, для задания траектории или скорости передвижения.

3. Jpeg алгоритм сжатия изображений.

---

Смотрите также файлы

• image394.docx

• Задание к лекции 2.docx

• Правовое регулирование рынка электронной коммерции.pptx

• Анализ исторической песни.docx

• .docx